Analytic Signal and Hilbert Transform
The hilbert function finds the exact analytic signal for a finite block of data. You can also generate the analytic signal by using an finite impulse response (FIR) Hilbert transformer filter to compute an approximation to the imaginary part.
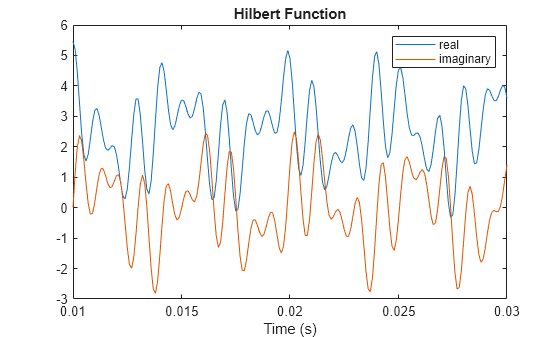
Generate a sequence composed of three sinusoids with frequencies 203, 721, and 1001 Hz. The sequence is sampled at 10 kHz for about 1 second. Use the hilbert function to compute the analytic signal. Plot it between 0.01 seconds and 0.03 seconds.
fs = 1e4; t = 0:1/fs:1; x = 2.5 + cos(2*pi*203*t) + sin(2*pi*721*t) + cos(2*pi*1001*t); y = hilbert(x); plot(t,real(y),t,imag(y)) xlim([0.01 0.03]) legend("real","imaginary") title("Hilbert Function") xlabel("Time (s)")
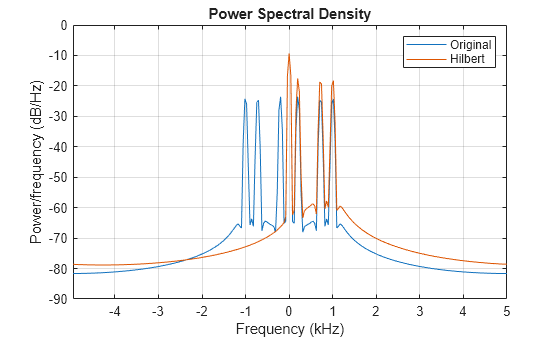
Compute Welch estimates of the power spectral densities of the original sequence and the analytic signal. Divide the sequences into Hamming-windowed, nonoverlapping sections of length 256. Verify that the analytic signal has no power at negative frequencies.
pwelch([x;y].',256,0,[],fs,"centered") legend("Original","Hilbert")
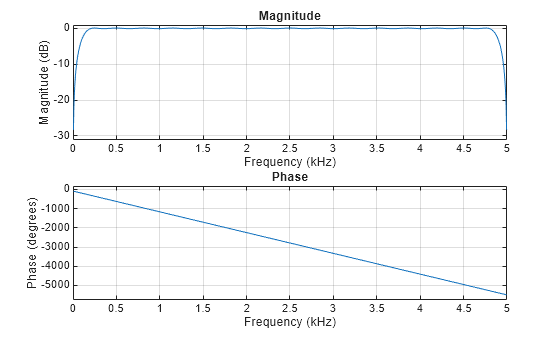
Use the designfilt function to design a 60th-order Hilbert transformer FIR filter. Specify a transition width of 400 Hz. Visualize the frequency response of the filter.
fo = 60; d = designfilt("hilbertfir",FilterOrder=fo, ... TransitionWidth=400,SampleRate=fs); freqz(d,1024,fs)
Filter the sinusoidal sequence to approximate the imaginary part of the analytic signal.
hb = filter(d,x);
The group delay of the filter, grd, is equal to one-half the filter order. Compensate for this delay. Remove the first grd samples of the imaginary part and the last grd samples of the real part and the time vector. Plot the result between 0.01 seconds and 0.03 seconds.
grd = fo/2; y2 = x(1:end-grd) + 1j*hb(grd+1:end); t2 = t(1:end-grd); plot(t2,real(y2),t2,imag(y2)) xlim([0.01 0.03]) legend("real","imaginary") title("FIR Filter") xlabel("Time (s)")

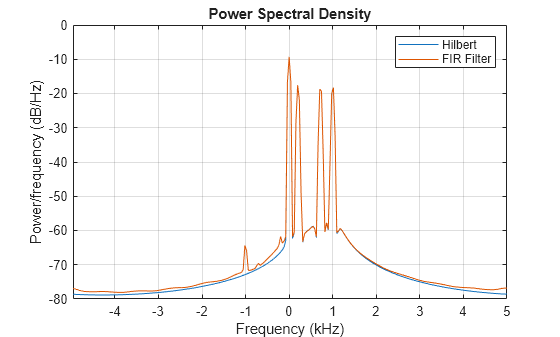
Estimate the power spectral density (PSD) of the approximate analytic signal and compare it to the hilbert result.
pwelch([y;[y2 zeros(1,grd)]].',256,0,[],fs,"centered") legend("Hilbert","FIR Filter")