plot
Compare simulation results to the training data, creating a time-course subplot for each group
Description
plot( displays a figure
showing the comparison between simulation results to the training data, with a
time-course subplot for each group.resultsObj)
plot(
uses additional options specified by one or more name-value arguments. resultsObj,Name,Value)
Examples
Load the sample data set.
load data10_32R.mat gData = groupedData(data); gData.Properties.VariableUnits = ["","hour","milligram/liter","milligram/liter"];
Create a two-compartment PK model.
pkmd = PKModelDesign; pkc1 = addCompartment(pkmd,"Central"); pkc1.DosingType = "Infusion"; pkc1.EliminationType = "linear-clearance"; pkc1.HasResponseVariable = true; pkc2 = addCompartment(pkmd,"Peripheral"); model = construct(pkmd); configset = getconfigset(model); configset.CompileOptions.UnitConversion = true; responseMap = ["Drug_Central = CentralConc","Drug_Peripheral = PeripheralConc"];
Provide model parameters to estimate.
paramsToEstimate = ["log(Central)","log(Peripheral)","Q12","Cl_Central"]; estimatedParam = estimatedInfo(paramsToEstimate,'InitialValue',[1 1 1 1]);
Assume every individual receives an infusion dose at time = 0, with a total infusion amount of 100 mg at a rate of 50 mg/hour.
dose = sbiodose("dose","TargetName","Drug_Central"); dose.StartTime = 0; dose.Amount = 100; dose.Rate = 50; dose.AmountUnits = "milligram"; dose.TimeUnits = "hour"; dose.RateUnits = "milligram/hour";
Estimate model parameters. By default, the function estimates a set of parameter for each individual (unpooled fit).
fitResults = sbiofit(model,gData,responseMap,estimatedParam,dose);
Plot the results.
plot(fitResults);
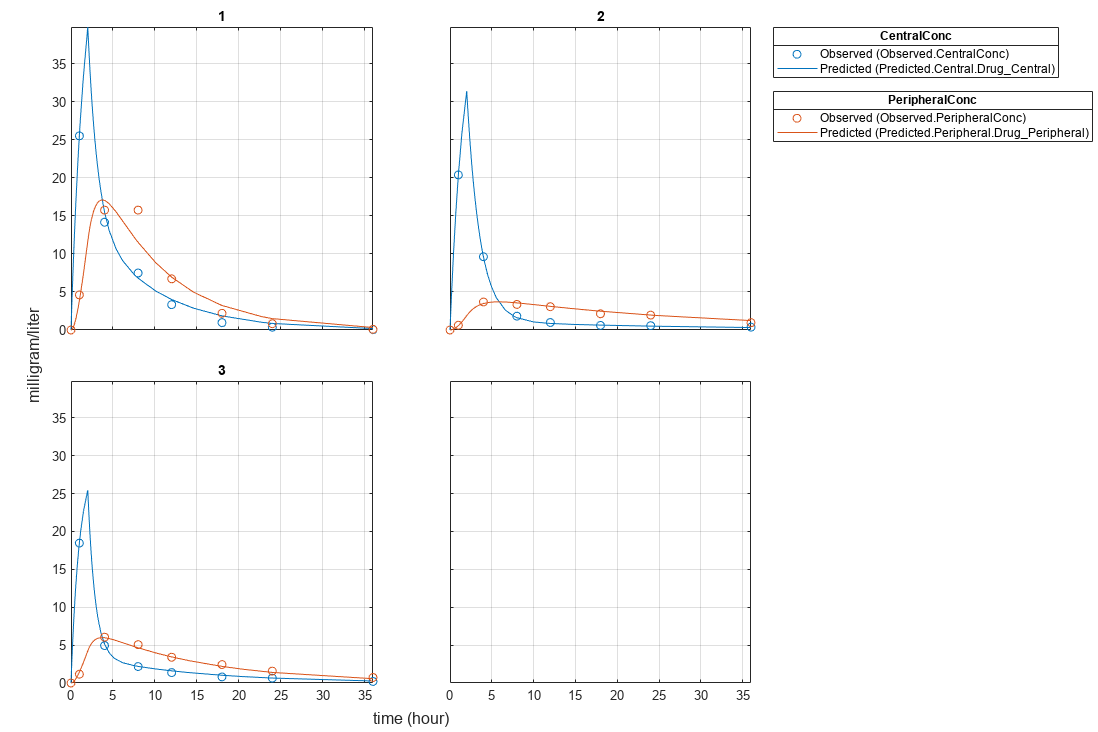
Plot all groups in one plot.
plot(fitResults,"PlotStyle","one axes");
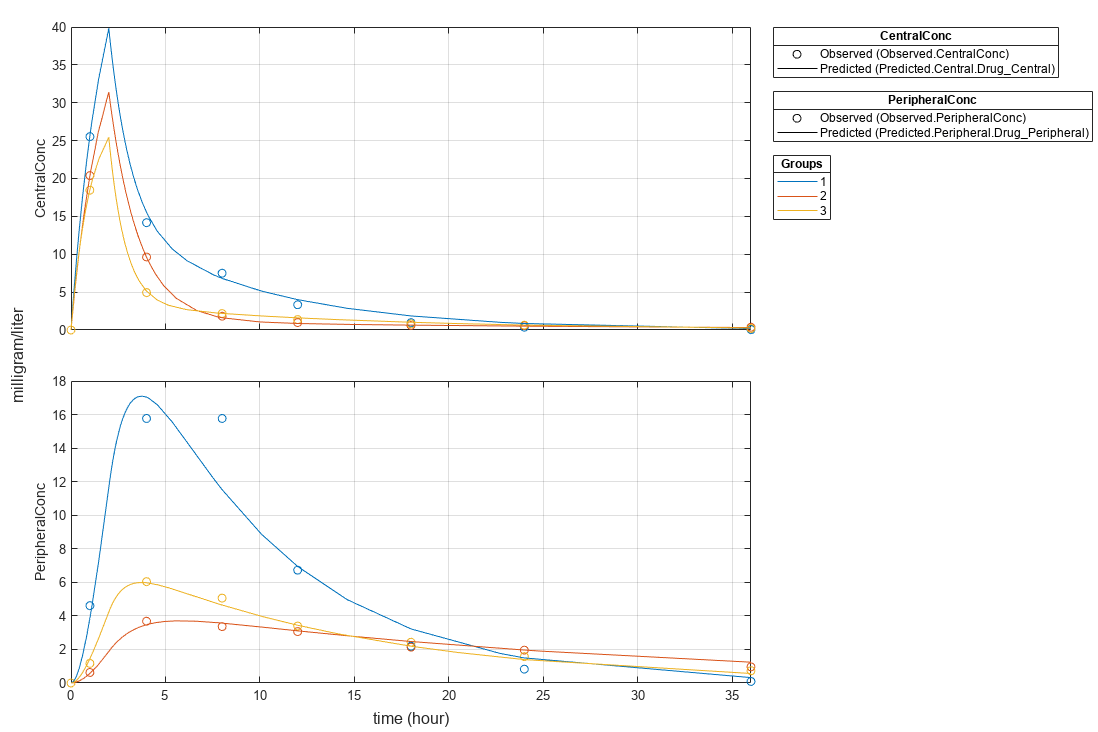
Change some axes properties.
s = struct; s.Properties.XGrid = "on"; s.Properties.YGrid = "on"; plot(fitResults,"PlotStyle","one axes","AxesStyle",s);
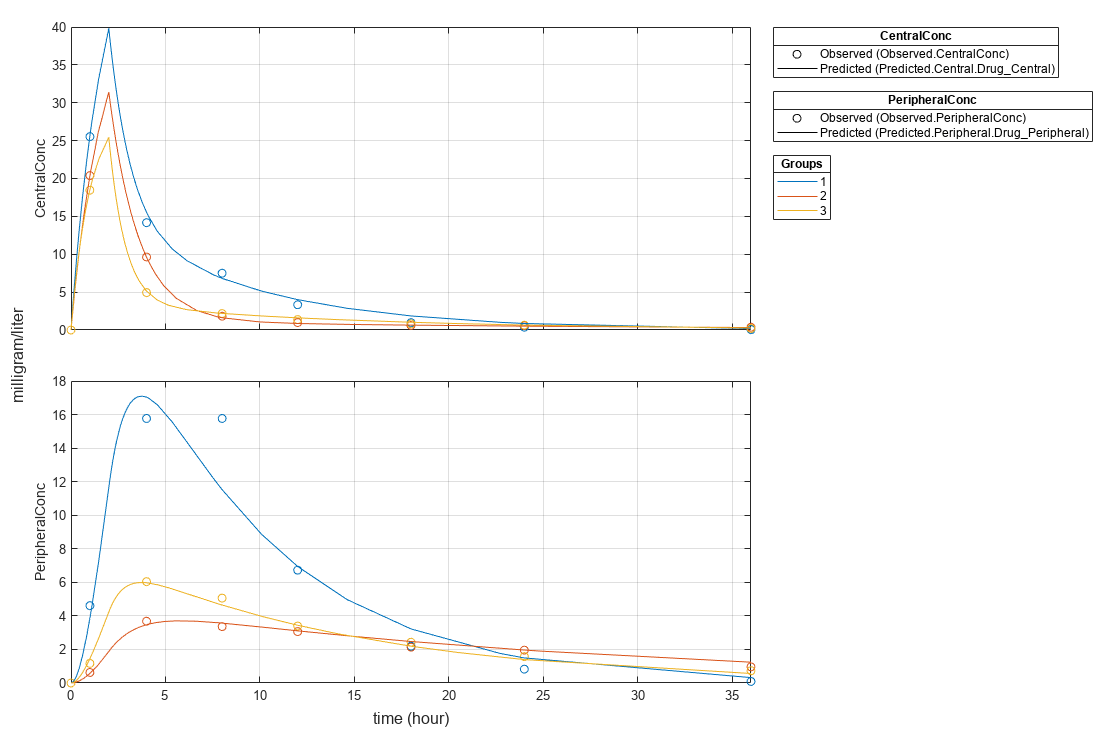
Compare the model predictions to the actual data.
plotActualVersusPredicted(fitResults)
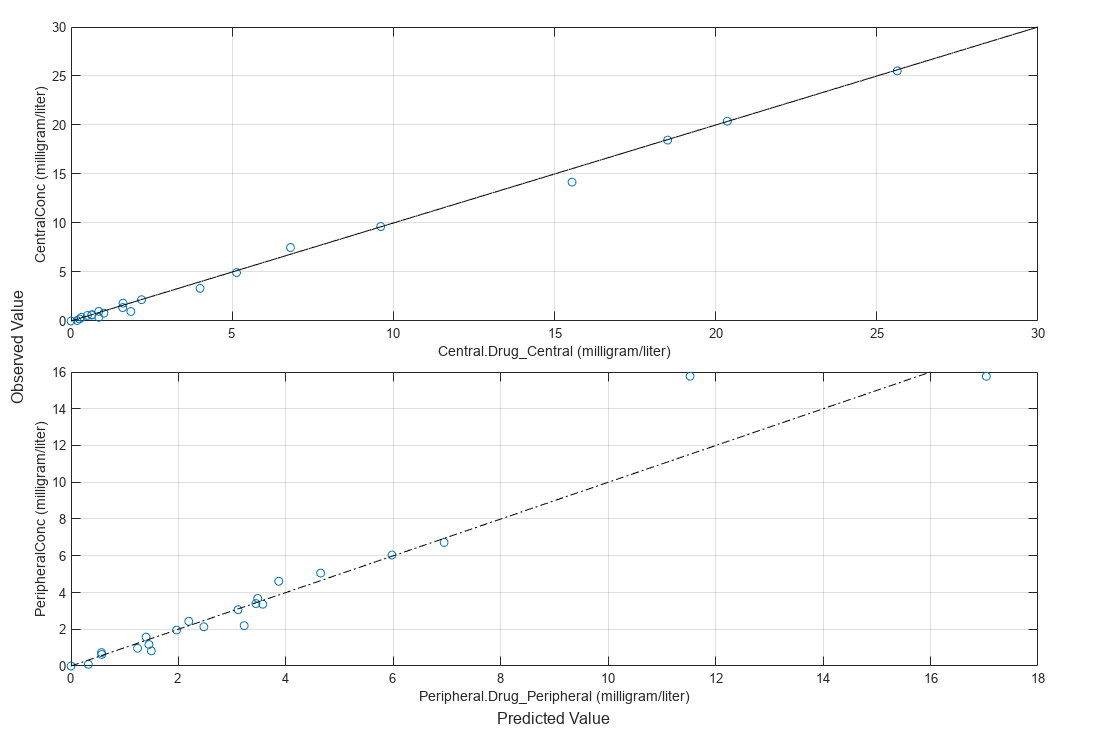
Use boxplot to show the variation of estimated model parameters.
boxplot(fitResults)
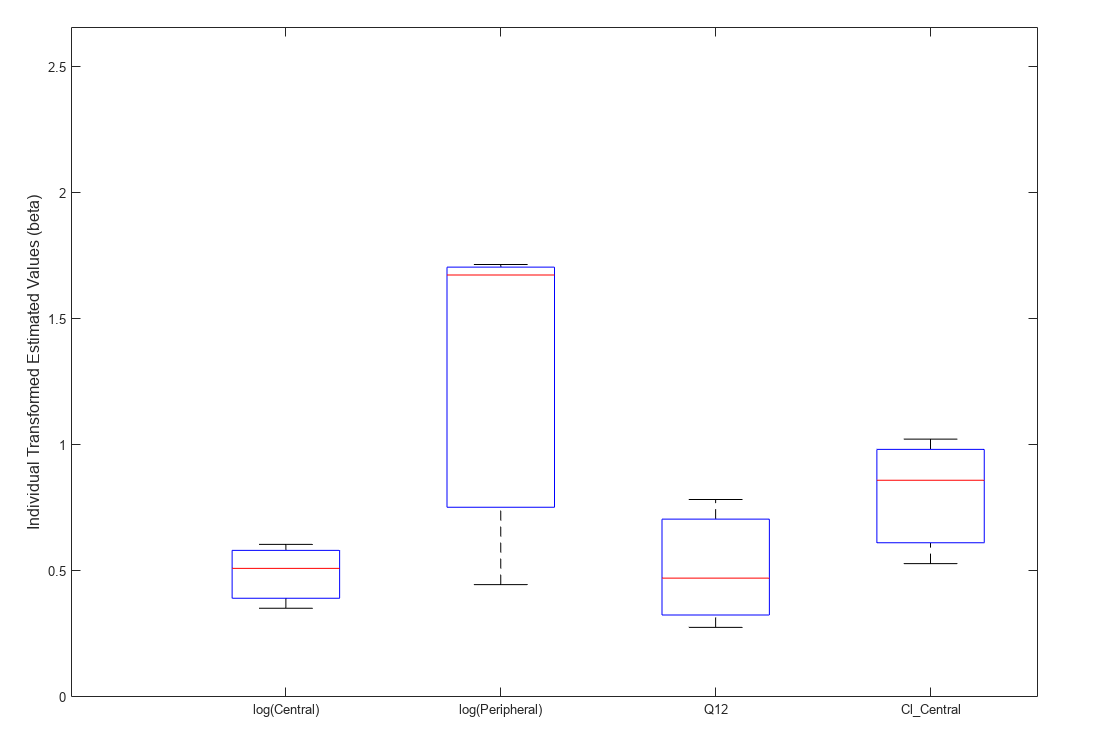
Plot the distribution of residuals. This normal probability plot shows the deviation from normality and the skewness on the right tail of the distribution of residuals. The default (constant) error model might not be the correct assumption for the data being fitted.
plotResidualDistribution(fitResults)
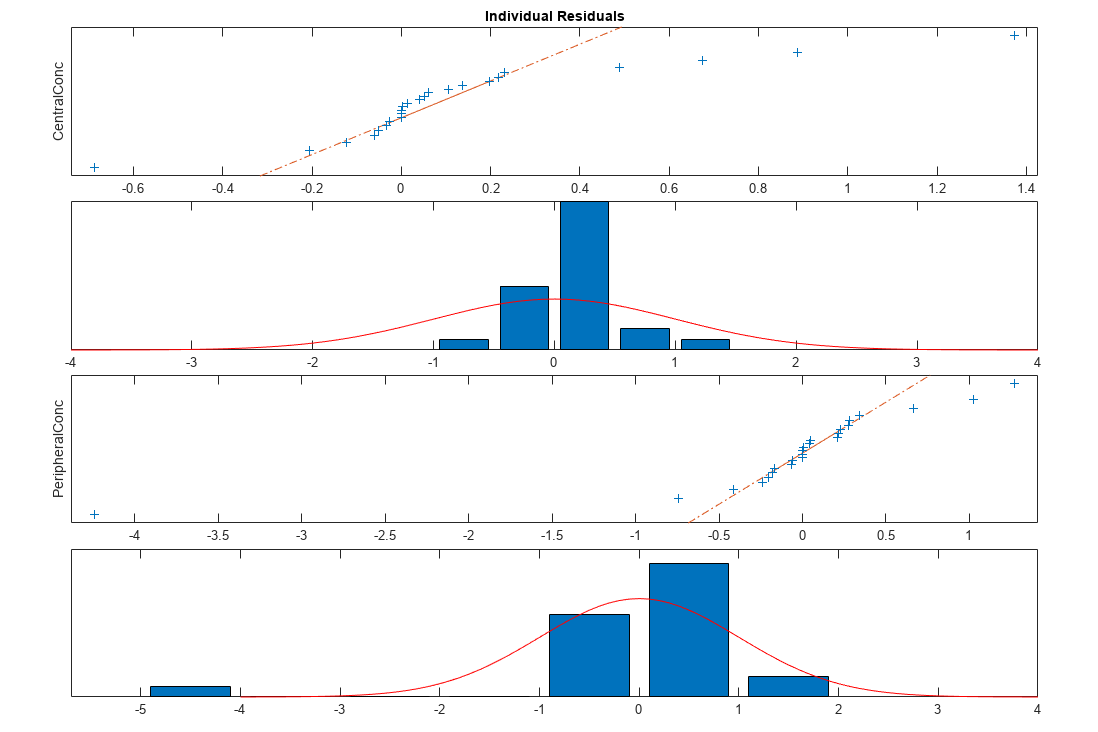
Plot residuals for each response using the model predictions on x-axis.
plotResiduals(fitResults,"Predictions")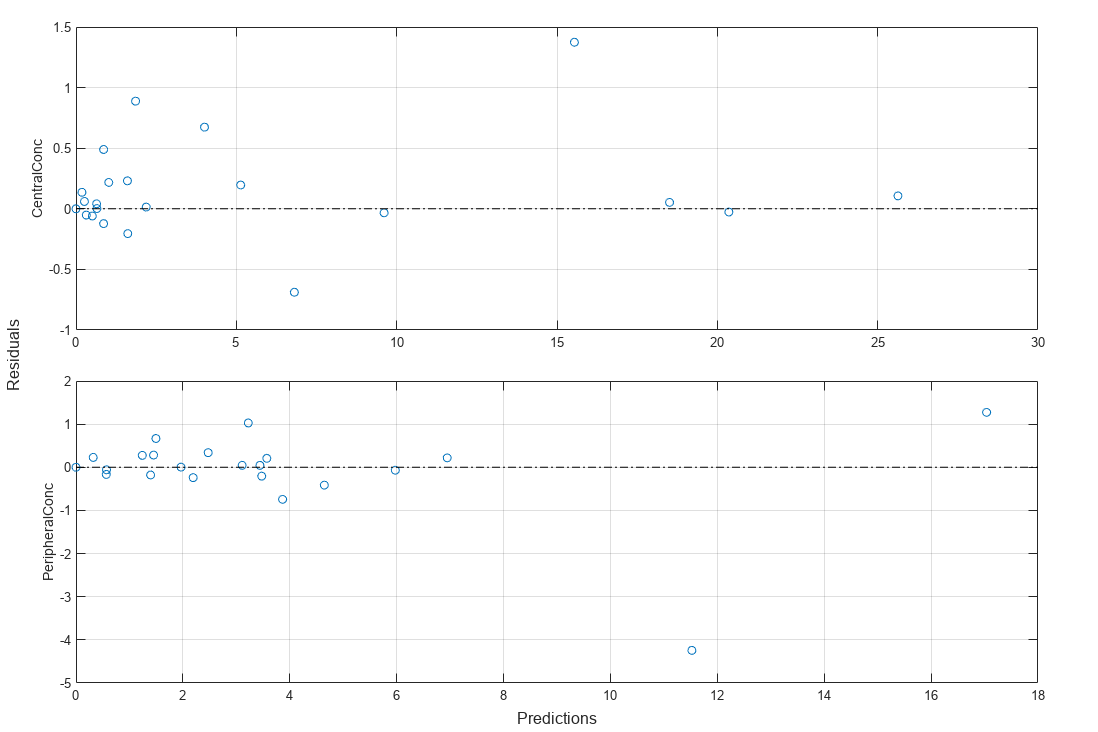
Get the summary of the fit results. stats.Name contains the name for each table from stats.Table, which contains a list of tables with estimated parameter values and fit quality statistics.
stats = summary(fitResults); stats.Name
ans = 'Unpooled Parameter Estimates'
ans = 'Statistics'
ans = 'Unpooled Beta'
ans = 'Residuals'
ans = 'Covariance Matrix'
ans = 'Error Model'
stats.Table
ans=3×9 table
Group Central Estimate Central StandardError Peripheral Estimate Peripheral StandardError Q12 Estimate Q12 StandardError Cl_Central Estimate Cl_Central StandardError
_____ ________________ _____________________ ___________________ ________________________ ____________ _________________ ___________________ ________________________
{'1'} 1.422 0.12334 1.5619 0.36355 0.47163 0.15196 0.5291 0.036978
{'2'} 1.8322 0.019672 5.3364 0.65327 0.2764 0.030799 0.86035 0.026257
{'3'} 1.6657 0.038529 5.5632 0.37063 0.78361 0.058657 1.0233 0.027311
ans=3×7 table
Group AIC BIC LogLikelihood DFE MSE SSE
_____ _______ _______ _____________ ___ ________ _______
{'1'} 60.961 64.051 -26.48 12 2.138 25.656
{'2'} -7.8379 -4.7475 7.9189 12 0.029012 0.34814
{'3'} -1.4336 1.6567 4.7168 12 0.043292 0.5195
ans=3×9 table
Group Central Estimate Central StandardError Peripheral Estimate Peripheral StandardError Q12 Estimate Q12 StandardError Cl_Central Estimate Cl_Central StandardError
_____ ________________ _____________________ ___________________ ________________________ ____________ _________________ ___________________ ________________________
{'1'} 0.35208 0.086736 0.44589 0.23277 0.47163 0.15196 0.5291 0.036978
{'2'} 0.60551 0.010737 1.6746 0.12242 0.2764 0.030799 0.86035 0.026257
{'3'} 0.51027 0.02313 1.7162 0.066621 0.78361 0.058657 1.0233 0.027311
ans=24×4 table
ID Time CentralConc PeripheralConc
__ ____ ___________ ______________
1 0 0 0
1 1 0.10646 -0.74394
1 4 1.3745 1.2726
1 8 -0.68825 -4.2435
1 12 0.67383 0.21806
1 18 0.88823 1.0269
1 24 0.48941 0.66755
1 36 0.13632 0.22948
2 0 0 0
2 1 -0.026731 -0.058311
2 4 -0.033299 -0.20544
2 8 -0.20466 0.20696
2 12 -0.12223 0.045409
2 18 0.041224 0.33883
2 24 -0.059498 0.0036257
2 36 -0.051645 0.27616
⋮
ans=12×6 table
Group Parameters Central Peripheral Q12 Cl_Central
_____ ______________ ___________ __________ ___________ ___________
{'1'} {'Central' } 0.015213 -0.022539 -0.0086672 0.001159
{'1'} {'Peripheral'} -0.022539 0.13217 0.045746 -0.0073135
{'1'} {'Q12' } -0.0086672 0.045746 0.023092 -0.0021484
{'1'} {'Cl_Central'} 0.001159 -0.0073135 -0.0021484 0.0013674
{'2'} {'Central' } 0.00038701 -0.002161 -0.00010177 9.7448e-05
{'2'} {'Peripheral'} -0.002161 0.42676 0.019101 -0.015755
{'2'} {'Q12' } -0.00010177 0.019101 0.00094857 -0.00073328
{'2'} {'Cl_Central'} 9.7448e-05 -0.015755 -0.00073328 0.00068942
{'3'} {'Central' } 0.0014845 -0.0054648 -0.0013216 0.00016639
{'3'} {'Peripheral'} -0.0054648 0.13737 0.016903 -0.0072722
{'3'} {'Q12' } -0.0013216 0.016903 0.0034406 -0.00082538
{'3'} {'Cl_Central'} 0.00016639 -0.0072722 -0.00082538 0.00074587
ans=3×5 table
Group Response ErrorModel a b
_____ __________ ____________ _______ ___
{'1'} {0×0 char} {'constant'} 1.2663 NaN
{'2'} {0×0 char} {'constant'} 0.14751 NaN
{'3'} {0×0 char} {'constant'} 0.18019 NaN
Input Arguments
Estimation results, specified as an OptimResults object or
NLINResults object, or
vector of results objects which contains estimation results from running
sbiofit.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: plot(fitResults,'PlotStyle','one axes') specifies to
plot data from each run into one axes instead of plotting each run individually as a
subplot.
Type of parameter estimates to plot, specified as
'individual'. For
LeastSquaresResults objects,
'individual' is the only option indicating to use
the individual parameter estimates to plot the simulation
results.
Data Types: char | string
Plot style, specified as 'trellis' or 'one
axes'. By default, the function plots the data from each
run into its own subplot. To plot all data into one plot, use
'one axes'.
Data Types: char | string
Axes properties, specified as a structure. The structure
(s) has the following field names and values
representing the axes properties.
| Field Name | Value |
|---|---|
s.Labels.Title | Character vector or string scalar. |
s.Labels.XLabel | Character vector or string scalar. |
s.Labels.YLabel | Character vector or string scalar. |
s.Properties.XGrid | 'off' (default) or
'on' |
s.Properties.XScale | 'linear' (default) or
'log' |
s.Properties.XDir | 'normal' (default) or
'reverse' |
s.Properties.XLim | Two-element vector of the form [min
max] |
s.Properties.YGrid | 'off' (default) or
'on' |
s.Properties.YScale | 'linear' (default) or
'log' |
s.Properties.YDir | 'normal' (default) or
'reverse' |
s.Properties.YLim | Two-element vector of the form [min
max] |
Data Types: structure
Version History
Introduced in R2014a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)