Block Linearization Troubleshooting

Once you identify blocks of interest in the linearization results for your Simulink^® model by querying the Linearization Advisor, you can troubleshoot the individual block linearizations. For more information on querying the Linearization Advisor and viewing block diagnostic information, see Identify and Fix Common Linearization Issues.

You can also troubleshoot individual block linearizations at the command line using a BlockDiagnostic object. For an example, see Troubleshoot Linearization Results at Command Line.

In Model Linearizer, on the Advisor tab, the detailed diagnostic information for a block linearization shows:

A diagnostic summary, showing any corresponding diagnostic messages, and a linearization summary table.
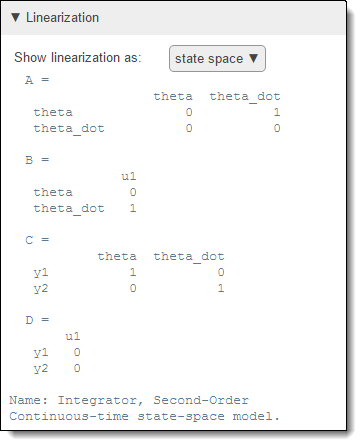
The block linearization value.
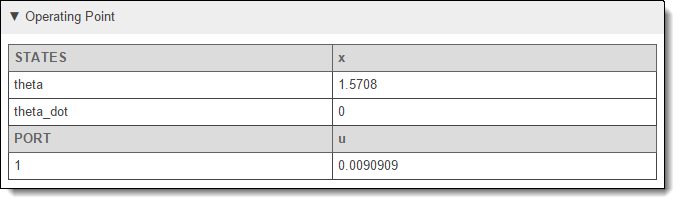
The block operating point; the state and input values for which the block is linearized.

You can diagnose potential linearization issues using this information.

Diagnostic Messages

Linearization diagnostic messages indicate blocks with properties or linearizations that correspond to common linearization problems. Fixing linearization issues identified in diagnostic messages is a good first step when troubleshooting your linearization.

Some block configurations that can generate diagnostic messages include:

Blocks with no predefined exact linearization and with non-floating-point signals or states. Such blocks linearize to zero and generate diagnostic messages.
Discontinuous blocks linearized at an operating point near a discontinuity. If such blocks are not treated as a gain during linearization, the software generates diagnostic messages regarding their linearization.
Blocks with least one input/output pair that linearizes to zero and that causes a zero input/output pair in the overall model linearization. A linearization has a zero input/output pair when a change in an input signal value does not produce a corresponding change in an output value.
Blocks that do not support linearization because they do not have a predefined exact linearization and do not support numerical perturbation.

Some diagnostic messages propose solutions to their corresponding linearization issues. For example, when an input signal is outside the saturation limits of a Saturation block, the diagnostic message proposes treating the block as a gain during linearization.

Linearization Summary

The linearization summary table displays the following properties of the block linearization:

Block Path — Location of the block in the Simulink model. To highlight the block in the model, click the block path.
Is On Path — Flag indicating whether the block is on the linearization path, that is, at least one linearization input is connected to at least one linearization output through the block. If you expect a block to be on the linearization path and it is not on the path, check the analysis point configuration in your model. Incorrectly placed linearization I/Os or loop openings can exclude blocks from the linearization path. Similarly, placing incorrect analysis points can unexpectedly add blocks to the linearization path.
Contributes to Linearization — Flag indicating whether the block numerically contributes to the overall model linearization. If a block unexpectedly does not contribute to the linearization result, investigate the linearization of the block and other blocks in the same branch of the linearization path. For example, if an adjacent block on the linearization path linearizes to zero, an otherwise correctly linearized block can be excluded from the linearization result.
Linearization method — The method used to linearize the model, specified as one of the following:
- Exact — The block linearization is computed using the defined analytic Jacobian of the block.
- Perturbation — The block does not have an analytic Jacobian. Instead, the block is linearized using numerical perturbation of its inputs and states. Some numerically perturbed blocks, such as those with discontinuities or non-floating-point input signals can linearize to zero.
- Block Substituted — The block linearization is specified using a custom block linearization. Consider checking that the specified block linearization is correct for your application. For more information, see Specify Block Linearization Using MATLAB Expression and Specify D-Matrix System for Block Linearization Using Function.
- Simscape Network — The block diagnostics correspond to a Simscape™ network in your model. For more information on linearizing and troubleshooting Simscape networks, see Linearize Simscape Networks.
- Not Supported — The block does not have an analytic Jacobian and does not support numerical perturbation. Specify the linearization for this block using a custom linearization. For more information, see Specify Block Linearization Using MATLAB Expression and Specify D-Matrix System for Block Linearization Using Function.

Block Linearization

To verify whether a block linearized as expected, check the block linearization equations. By default the software displays the linearization in state-space format. In the Show linearization as drop-down list, you can select a different display format.

To diagnose the cause of an unexpected block linearization, such as a block that linearizes to zero, consider:

Any corresponding diagnostic messages. These messages can highlight common causes of incorrect linearizations and propose potential solutions.
The block operating point. For example, if the input to a saturation block is outside the saturation limits of the block, the block linearizes to zero.
The block parameters. For example, if a block is configured to use non-floating-point inputs or states and has no predefined exact linearization, it linearizes to zero.

Block Operating Point

If the block does not linearize as expected, check the operating point at which the block is linearized, which consists of input and state values. If the operating point for the block is incorrect, check whether the overall model operating point is correct. For more information, see Check Operating Point.

If an input signal value in the block operating point is incorrect, investigate the linearization of upstream blocks from that signal. For example, consider a Product block with two inputs. The operating point of this block consists of the two input signal values. If either input value is zero, the path from the other input to the output linearizes to zero.

If you expect the Product block to contribute to the linearization result for the operating point at which you linearized the model, check the linearization for the block that generates the zero input signal. For complex models, the cause of the incorrect input signal can be more than one block upstream.

Common Problematic Blocks

Some Simulink blocks have properties that cause them to linearize poorly. Often, such blocks either linearize to zero or have linearization diagnostic messages associated with them. Therefore, the Linearization Advisor identifies them as potentially problematic blocks when the Advisor tab first opens.

The following table shows some blocks that commonly cause linearization issues and proposes potential fixes for each block. All these blocks have corresponding diagnostic messages.

Block Type	Linearization Issue	Possible Fix
Blocks that do not support linearization	Some blocks are implemented without defined analytic Jacobians and do not support numerical perturbation.	Specify a custom block linearization. For examples, see Specify Block Linearization Using MATLAB Expression and Specify D-Matrix System for Block Linearization Using Function.
Blocks with discontinuities	Blocks with discontinuities typically have poor linearization results when the operating point is near the discontinuity.	Treat the block as a gain of `1` during linearization. To do so, select the Treat as gain when linearizing block parameter. Specify a custom block linearization. For examples, see Specify Block Linearization Using MATLAB Expression and Specify D-Matrix System for Block Linearization Using Function.
Event-Based Subsystems (triggered subsystems)	Blocks within event-based subsystems linearize to zero because such subsystems do not trigger during linearization.	When possible, specify a custom event-based subsystem linearization as a lumped average model or periodic function call subsystem. For more information, see Linearize Event-Based Subsystems (Externally Scheduled Subsystems).
Blocks with non-floating-point signals	Blocks that have non-floating-point input signals or states and do not have defined analytic Jacobians linearize to zero.	Convert the non-floating-point data types to either double precision or single precision.. For more information, see Linearize Blocks with Non-Floating-Point Signals or States.
Blocks that linearize using numerical perturbation rather than defined analytic Jacobians	Blocks that are located near discontinuous regions, such as S-Functions, MATLAB function blocks, or lookup tables, are sensitive to numerical perturbation levels. If the perturbation level is too small, the block linearizes to zero.	Change the numerical perturbation level of the block. For more information, see Change Perturbation Level of Blocks Perturbed During Linearization.