incrementalClassificationECOC
Multiclass classification model using binary learners for incremental learning
Since R2022a
Description
The incrementalClassificationECOC function creates an
incrementalClassificationECOC model object, which represents a multiclass error-correcting output codes (ECOC)
classification model that uses binary learners for incremental learning.
Unlike other Statistics and Machine Learning Toolbox™ model objects, incrementalClassificationECOC can be called directly. Also,
you can specify learning options, such as performance metrics configurations and prior class
probabilities, before fitting the model to data. After you create an
incrementalClassificationECOC object, it is prepared for incremental learning.
incrementalClassificationECOC is best suited for incremental learning. For a traditional
approach to training a multiclass classification model (such as creating a model by fitting it
to data, performing cross-validation, tuning hyperparameters, and so on), see fitcecoc.
Creation
You can create an incrementalClassificationECOC model object in several ways:
Call the function directly — Configure incremental learning options, or specify learner-specific options, by calling
incrementalClassificationECOCdirectly. This approach is best when you do not have data yet or you want to start incremental learning immediately. You must specify the maximum number of classes or all class names expected in the response data during incremental learning.Convert a traditionally trained model — To initialize a multiclass ECOC classification model for incremental learning using the model parameters of a trained model object (
ClassificationECOCorCompactClassificationECOC), you can convert the traditionally trained model to anincrementalClassificationECOCmodel object by passing it to theincrementalLearnerfunction.Call an incremental learning function —
fit,updateMetrics, andupdateMetricsAndFitaccept a configuredincrementalClassificationECOCmodel object and data as input, and return anincrementalClassificationECOCmodel object updated with information learned from the input model and data.
Syntax
Description
Mdl = incrementalClassificationECOC(MaxNumClasses=maxNumClasses)Mdl, where MaxNumClasses is the maximum number
of classes expected in the response data during incremental learning. Properties of a
default model contain placeholders for unknown model parameters. You must train a default
model before you can track its performance or generate predictions from it.
Mdl = incrementalClassificationECOC(ClassNames=classNames)ClassNames expected in the response data
during incremental learning, and sets the ClassNames property.
Mdl = incrementalClassificationECOC(___,Name=Value)incrementalClassificationECOC(MaxNumClasses=5,Coding="onevsone",MetricsWarmupPeriod=100)
sets the maximum number of classes expected in the response data to 5,
specifies to use a one-versus-one coding design, and sets the metrics warm-up period to
100.
Input Arguments
Maximum number of classes expected in the response data during incremental learning, specified as a positive integer.
MaxNumClasses sets the number of class names in the ClassNames property.
If you do not specify MaxNumClasses, you must specify the
ClassNames argument.
Example: MaxNumClasses=5
Data Types: single | double
All unique class labels expected in the response data during incremental learning,
specified as a categorical, character, or string array; logical or numeric vector; or
cell array of character vectors. ClassNames and the response data
must have the same data type. This argument sets the ClassNames property.
ClassNames specifies the order of any input or output
argument dimension that corresponds to the class order. For example, set
ClassNames to
specify the column
order of classification scores returned by predict.
If you do not specify ClassNames, you must specify the
MaxNumClasses argument. In that case, the software infers the
ClassNames property from the data during incremental
learning.
Example: ClassNames=["virginica","setosa","versicolor"]
Data Types: single | double | logical | string | char | cell | categorical
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: NumPredictors=4,Prior=[0.3 0.3 0.4] specifies the number of
predictor variables as 4 and sets the prior class probability
distribution to [0.3 0.3 0.4].
Coding design name, specified as a numeric matrix or a value in this table.
| Value | Number of Binary Learners | Description |
|---|---|---|
"allpairs" and "onevsone" | K(K – 1)/2 | For each binary learner, one class is positive, another is negative, and the software ignores the rest. This design exhausts all combinations of class pair assignments. |
"binarycomplete" | This design partitions the classes into all binary combinations, and
does not ignore any classes. For each binary learner, all class assignments
are –1 and 1 with at least one
positive class and one negative class in the assignment. | |
"denserandom" | Random, but approximately 10 log2K | For each binary learner, the software randomly assigns classes into positive or negative classes, with at least one of each type. For more details, see Random Coding Design Matrices. |
"onevsall" | K | For each binary learner, one class is positive and the rest are negative. This design exhausts all combinations of positive class assignments. |
"ordinal" | K – 1 | For the first binary learner, the first class is negative and the rest are positive. For the second binary learner, the first two classes are negative and the rest are positive, and so on. |
"sparserandom" | Random, but approximately 15 log2K | For each binary learner, the software randomly assigns classes as positive or negative with probability 0.25 for each, and ignores classes with probability 0.5. For more details, see Random Coding Design Matrices. |
"ternarycomplete" | This design partitions the classes into all ternary combinations. All
class assignments are 0, –1, and
1 with at least one positive class and one negative
class in each assignment. |
You can also specify a coding design using a custom coding matrix, which is a
K-by-L matrix. Each row corresponds to a
class and each column corresponds to a binary learner. The class order (rows)
corresponds to the order in the ClassNames property. Create the matrix by following these guidelines:
Every element of the custom coding matrix must be
–1,0, or1, and the value must correspond to a dichotomous class assignment. ConsiderCoding(i,j), the class that learnerjassigns to observations in classi.Value Dichotomous Class Assignment –1Learner jassigns observations in classito a negative class.0Before training, learner jremoves observations in classifrom the data set.1Learner jassigns observations in classito a positive class.Every column must contain at least one
–1and one1.For all column indices
i,jwherei≠j,Coding(:,i)cannot equalCoding(:,j), andCoding(:,i)cannot equal–Coding(:,j).All rows of the custom coding matrix must be different.
For more details on the form of custom coding design matrices, see Custom Coding Design Matrices.
Example: Coding="ternarycomplete"
Data Types: char | string | double | single | int16 | int32 | int64 | int8
Model performance metrics to track during incremental learning, specified as
"classiferror" (classification error, or
misclassification error rate), a function handle (for example,
@metricName), a structure array of function handles, or a cell
vector of names, function handles, or structure arrays.
When Mdl is warm (see IsWarm), updateMetrics and updateMetricsAndFit track performance metrics in the Metrics property of
Mdl.
To specify a custom function that returns a performance metric, use function handle notation. The function must have this form.
metric = customMetric(C,S)
The output argument
metricis an n-by-1 numeric vector, where each element is the loss of the corresponding observation in the data processed by the incremental learning functions during a learning cycle.You specify the function name (here,
customMetric).Cis an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs, where K is the number of classes. The column order corresponds to the class order in theClassNamesproperty. CreateCby settingC(=p,q)1, if observationpqp0.Sis an n-by-K numeric matrix of predicted classification scores.Sis similar to theNegLossoutput ofpredict, where rows correspond to observations in the data and the column order corresponds to the class order in theClassNamesproperty.S(is the classification score of observationp,q)pq
To specify multiple custom metrics and assign a custom name to each, use a structure array. To specify a combination of built-in and custom metrics, use a cell vector.
updateMetrics and updateMetricsAndFit store
specified metrics in a table in the Metrics property. The data type of Metrics determines the
row names of the table.
Metrics Value Data Type | Description of Metrics Property Row Name | Example |
|---|---|---|
| String or character vector | Name of corresponding built-in metric | Row name for "classiferror" is
"ClassificationError" |
| Structure array | Field name | Row name for struct(Metric1=@customMetric1) is
"Metric1" |
| Function handle to function stored in a program file | Name of function | Row name for @customMetric is
"customMetric" |
| Anonymous function | CustomMetric_, where
Metrics | Row name for @(C,S)customMetric(C,S)... is
CustomMetric_1 |
For more details on performance metrics options, see Performance Metrics.
Example: Metrics=struct(Metric1=@customMetric1,Metric2=@customMetric2)
Example: Metrics={@customMetric1,@customMetric2,"classiferror",struct(Metric3=@customMetric3)}
Data Types: char | string | struct | cell | function_handle
Binary learner templates, specified as "linear",
"kernel", an incremental learning object, a template object, or
a cell array of supported incremental learning objects and template objects.
"linear"or"kernel"— Specify theLearnersvalue as a string scalar or character vector to use the default linear learners or default kernel learners (defaultincrementalClassificationLinearorincrementalClassificationKernelobjects, respectively).Incremental learning object (
incrementalClassificationLinearorincrementalClassificationKernelobject) — Configure binary learner properties (both model-specific properties and incremental learning properties) when you create an incremental learning object, and pass the object toincrementalClassificationECOCas theLearnersvalue.Template object returned by the
templateLinear,templateSVM, ortemplateKernelfunction — Configure model-specific properties when you create a template object, and pass the object toincrementalClassificationECOCas theLearnersvalue. Use this approach to specify model properties with a template object and to use the default incremental learning options.Cell array of supported incremental learning objects and template objects — Use this approach to customize each learner individually.
You cannot specify the ClassNames (class names) and Prior
(prior class probabilities) properties for an
incrementalClassificationECOC object by using the binary
learners. Instead, specify the properties by using the corresponding name-value
arguments of incrementalClassificationECOC.
Example: Learners="kernel"
Flag for updating the metrics of binary learners, specified as logical 0 (false) or 1 (true).
If the value is true, the software tracks the performance metrics
of binary learners using the Metrics property of the binary learners,
stored in the BinaryLearners property. For an example, see Configure Incremental Model to Track Performance Metrics for Model and Binary Learners.
Example: UpdateBinaryLearnerMetrics=true
Data Types: logical
Properties
You can set most properties by using name-value argument syntax when you call
incrementalClassificationECOC directly. You cannot set the properties
BinaryLearners, CodingMatrix,
CodingName, NumTrainingObservations, and
IsWarm using name-value argument syntax with the arguments of the same
names. However, you can set CodingMatrix and
CodingName by using the Coding name-value
argument, and you can set BinaryLearners by using the
Learners name-value argument.
You can set some properties when you call incrementalLearner
to convert a traditionally trained model.
Classification Model Parameters
This property is read-only.
Trained binary learners, specified as a cell array of incrementalClassificationLinear or incrementalClassificationKernel model objects. The number of binary
learners depends on the coding design.
The software trains BinaryLearner{j} according to the binary
problem specified by CodingMatrix(:,j).
The default BinaryLearners value depends on how you create
the model:
If you convert a traditionally trained model (for example,
TTMdl) to createMdl,BinaryLearnerscontains incremental learners converted from the binary learners inTTMdl.When you train
TTMdl, you must specify theLearnersname-value argument offitcecocto use support vector machine (SVM) binary learner templates (templateSVM) or linear classification model binary learner templates (templateLinear).Otherwise, the
Learnersname-value argument sets this property. The default value of the argument is"linear", which usesincrementalClassificationLinearmodel objects with SVM learners.
Data Types: cell
This property is read-only.
Binary learner loss function, specified as a built-in loss function name or
function handle. incrementalClassificationECOC stores the
BinaryLoss value as a character vector or function
handle.
This table describes the built-in functions, where yj is the class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss formula.
Value Description Score Domain g(yj,sj) "binodeviance"Binomial deviance (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"Exponential (–∞,∞) exp(–yjsj)/2 "hamming"Hamming [0,1] or (–∞,∞) [1 – sign(yjsj)]/2 "hinge"Hinge (–∞,∞) max(0,1 – yjsj)/2 "linear"Linear (–∞,∞) (1 – yjsj)/2 "logit"Logistic (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"Quadratic [0,1] [1 – yj(2sj – 1)]2/2 The software normalizes binary losses so that the loss is 0.5 when yj = 0. Also, the software calculates the mean binary loss for each class [1].
For a custom binary loss function, for example
customFunction, specify its function handleBinaryLoss=@customFunction.customFunctionhas this form:bLoss = customFunction(M,s)
Mis the K-by-B coding matrix stored inMdl.CodingMatrix.sis the 1-by-B row vector of classification scores.bLossis the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.K is the number of classes.
B is the number of binary learners.
For an example of a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function. This example is for a traditionally trained model. You can define a custom loss function for incremental learning as shown in the example.
For more information, see Binary Loss.
The default BinaryLoss value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl,BinaryLossis specified by the corresponding property of the traditionally trained model. You can also specify theBinaryLossvalue by using theBinaryLossname-value argument ofincrementalLearner.Otherwise, the default value of
BinaryLossis"hinge".
Data Types: char | string | function_handle
This property is read-only.
All unique class labels expected in the response data during incremental learning, specified as a categorical or character array, a logical or numeric vector, or a cell array of character vectors.
You can set ClassNames in one of three ways:
If you specify the
MaxNumClassesargument, the software infers theClassNamesproperty during incremental learning.If you specify the
ClassNamesargument,incrementalClassificationECOCstores your specification in theClassNamesproperty. (The software treats string arrays as cell arrays of character vectors.)If you convert a traditionally trained model to create
Mdl, theClassNamesproperty is specified by the corresponding property of the traditionally trained model.
Data Types: single | double | logical | char | string | cell | categorical
This property is read-only.
Class assignment codes for the binary learners, specified as a numeric matrix.
CodingMatrix is a K-by-L
matrix, where K is the number of classes and L
is the number of binary learners.
The elements of CodingMatrix are –1,
0, and 1, and the values correspond to
dichotomous class assignments. This table describes how learner j
assigns observations in class i to a dichotomous class
corresponding to the value of CodingMatrix(i,j).
| Value | Dichotomous Class Assignment |
|---|---|
–1 | Learner j assigns observations in class i to a negative
class. |
0 | Before training, learner j removes observations
in class i from the data set. |
1 | Learner j assigns observations in class i to a positive
class. |
For details, see Coding Design.
The default CodingMatrix value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl,CodingMatrixis specified by the corresponding property of the traditionally trained model.Otherwise, the
Codingname-value argument sets this property. The default value of the argument uses the one-versus-one coding design.
Data Types: double | single | int8 | int16 | int32 | int64
This property is read-only.
Coding design name, specified as a character vector.
The default CodingName value depends on how you create the model:
If you convert a full, traditionally trained model (
ClassificationECOC) to createMdl,CodingNameis specified by the corresponding property of the traditionally trained model.If you convert a compact, traditionally trained model (
CompactClassificationECOC) to createMdl,CodingNameis"converted".Otherwise, the
Codingname-value argument sets this property. The default value of the argument is"onevsone". If you specify a custom coding matrix usingCoding,CodingNameis"custom".
For details, see Coding Design.
Data Types: char
This property is read-only.
Decoding scheme, specified as "lossweighted" or
"lossbased". incrementalClassificationECOC stores the
Decoding value as a character vector.
The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation. The software supports two decoding schemes:
"lossweighted"— The predicted class of an observation corresponds to the class that produces the minimum sum of the binary losses over binary learners."lossbased"— The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over binary learners.
For more information, see Binary Loss.
The default Decoding value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl, theDecodingname-value argument ofincrementalLearnersets this property. The default value of the argument is"lossweighted".Otherwise, the default value of
Decodingis"lossweighted".
Data Types: char | string
This property is read-only.
Number of predictor variables, specified as a nonnegative numeric scalar.
The default NumPredictors value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl,NumPredictorsis specified by the corresponding property of the traditionally trained model.If you create
Mdlby callingincrementalClassificationECOCdirectly, you can specifyNumPredictorsby using name-value argument syntax. If you do not specify the value, then the default value is0, and incremental fitting functions inferNumPredictorsfrom the predictor data during training.
Data Types: double
This property is read-only.
Number of observations fit to the incremental model Mdl, specified as a nonnegative numeric scalar. NumTrainingObservations increases when you pass Mdl and training data to fit or updateMetricsAndFit.
Note
If you convert a traditionally trained model to create Mdl, incrementalClassificationECOC does not add the number of observations fit to the traditionally trained model to NumTrainingObservations.
Data Types: double
This property is read-only.
Prior class probabilities, specified as "empirical",
"uniform", or a numeric vector. incrementalClassificationECOC
stores the Prior value as a numeric vector.
| Value | Description |
|---|---|
"empirical" | Incremental learning functions infer prior class probabilities from the observed class relative frequencies in the response data during incremental training. |
"uniform" | For each class, the prior probability is 1/K, where K is the number of classes. |
| numeric vector | Custom, normalized prior probabilities. The order of the elements of
Prior corresponds to the elements of the
ClassNames property. |
The default Prior value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl,Prioris specified by the corresponding property of the traditionally trained model.Otherwise, the default value is
"empirical".
Data Types: single | double | char | string
This property is read-only.
Score transformation function to apply to the predicted scores, specified as
'none'. An ECOC model does not support score transformation.
Performance Metrics Parameters
Flag indicating whether the incremental model tracks performance metrics, specified as logical
0 (false) or 1
(true).
The incremental model Mdl is warm
(IsWarm becomes true) when incremental fitting
functions perform both of these actions:
Fit the incremental model to
MetricsWarmupPeriodobservations.Process
MaxNumClassesclasses or all class names specified by theClassNamesname-value argument.
| Value | Description |
|---|---|
true or 1 | The incremental model Mdl is warm. Consequently, updateMetrics and updateMetricsAndFit track performance metrics in the Metrics property of Mdl. |
false or 0 | updateMetrics and updateMetricsAndFit do not track performance metrics. |
Data Types: logical
This property is read-only.
Model performance metrics updated during incremental learning by
updateMetrics and updateMetricsAndFit,
specified as a table with two columns and m rows, where
m is the number of metrics specified by the Metrics name-value
argument.
The columns of Metrics are labeled Cumulative and Window.
Cumulative: Elementjis the model performance, as measured by metricj, from the time the model became warm (IsWarmis1).Window: Elementjis the model performance, as measured by metricj, evaluated over all observations within the window specified by theMetricsWindowSizeproperty. The software updatesWindowafter it processesMetricsWindowSizeobservations.
Rows are labeled by the specified metrics. For details, see the
Metrics name-value argument of
incrementalLearner or incrementalClassificationECOC.
Data Types: table
This property is read-only.
Number of observations the incremental model must be fit to before it tracks performance metrics in its Metrics property, specified as a nonnegative integer.
The default MetricsWarmupPeriod value depends on how you create
the model:
If you convert a traditionally trained model to create
Mdl, theMetricsWarmupPeriodname-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is0.Otherwise, the default value is
1000.
For more details, see Performance Metrics.
Data Types: single | double
This property is read-only.
Number of observations to use to compute window performance metrics, specified as a positive integer.
The default MetricsWindowSize value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl, theMetricsWindowSizename-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is200.Otherwise, the default value is
200.
For more details on performance metrics options, see Performance Metrics.
Data Types: single | double
Object Functions
fit | Train ECOC classification model for incremental learning |
updateMetricsAndFit | Update performance metrics in ECOC incremental learning classification model given new data and train model |
updateMetrics | Update performance metrics in ECOC incremental learning classification model given new data |
loss | Loss of ECOC incremental learning classification model on batch of data |
predict | Predict responses for new observations from ECOC incremental learning classification model |
perObservationLoss | Per observation classification error of model for incremental learning |
reset | Reset incremental classification model |
Examples
To create an ECOC classification model for incremental learning, you must specify the maximum number of classes that you expect the model to process (MaxNumClasses name-value argument). As you fit the model to incoming batches of data by using an incremental fitting function, the model collects new classes in its ClassNames property. If the specified maximum number of classes is inaccurate, one of the following occurs:
Before an incremental fitting function processes the expected maximum number of classes, the model is cold. Consequently, the
updateMetricsandupdateMetricsAndFitfunctions do not measure performance metrics.If the number of classes exceeds the maximum expected, the incremental fitting function issues an error.
This example shows how to create an ECOC model for incremental learning when the only information you specify is the expected maximum number of classes in the data. Also, the example illustrates the consequences when incremental fitting functions process all expected classes early and late in the sample.
For this example, consider training a device to predict whether a subject is sitting, standing, walking, running, or dancing based on biometric data measured on the subject. Therefore, the device has a maximum of 5 classes from which to choose.
Process Expected Maximum Number of Classes Early in Sample
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Create an incremental ECOC model for multiclass learning. Specify a maximum of 5 classes in the data.
MdlEarly = incrementalClassificationECOC(MaxNumClasses=5)
MdlEarly =
incrementalClassificationECOC
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1×0 double]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
MdlEarly is an incrementalClassificationECOC model object. All its properties are read-only. MdlEarly must be fit to data before you can use it to perform any other operations.
Display the coding design matrix.
MdlEarly.CodingMatrix
ans = 5×10
1 1 1 1 0 0 0 0 0 0
-1 0 0 0 1 1 1 0 0 0
0 -1 0 0 -1 0 0 1 1 0
0 0 -1 0 0 -1 0 -1 0 1
0 0 0 -1 0 0 -1 0 -1 -1
Each row of the coding design matrix corresponds to a class, and each column corresponds to a binary learner. For example, the first binary learner is for classes 1 and 2, and the fourth binary learner is for classes 1 and 5, where both learners assume class 1 as a positive class.
Fit the incremental model to the training data by using the updateMetricsAndFit function. Simulate a data stream by processing chunks of 50 observations at a time. At each iteration:
Process 50 observations.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
Store the first model coefficient of the first binary learner , the cumulative metrics, and the window metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); mc = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); beta11 = zeros(nchunk+1,1); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; MdlEarly = updateMetricsAndFit(MdlEarly,X(idx,:),Y(idx)); mc{j,:} = MdlEarly.Metrics{"ClassificationError",:}; beta11(j) = MdlEarly.BinaryLearners{1}.Beta(1); end
MdlEarly is an incrementalClassificationECOC model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.
To see how the performance metrics and evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(beta11) ylabel("\beta_{11}") xlim([0 nchunk]) nexttile plot(mc.Variables) xlim([0 nchunk]) ylabel("Classification Error") xline(MdlEarly.MetricsWarmupPeriod/numObsPerChunk,"--") legend(mc.Properties.VariableNames) xlabel(t,"Iteration")

The plots indicate that updateMetricsAndFit performs the following actions:
Fit during all incremental learning iterations.
Compute the performance metrics after the metrics warm-up period (dashed vertical line) only.
Compute the cumulative metrics during each iteration.
Compute the window metrics after processing 200 observations (4 iterations).
Process Expected Maximum Number of Classes Late in Sample
Rearrange the data set so that only the last 5000 samples contain the observations labeled with class 5.
Move all observations labeled with class 5 to the end of the sample.
idx5 = Y == 5; Xnew = [X(~idx5,:); X(idx5,:)]; Ynew = [Y(~idx5); Y(idx5)]; sum(idx5)
ans = 2653
Shuffle the last 5000 samples.
m = 5000; idx_shuffle = randsample(m,m); Xnew(end-m+1:end,:) = Xnew(end-m+idx_shuffle,:); Ynew(end-m+1:end) = Ynew(end-m+idx_shuffle);
An ECOC model trains a binary learner only when an incoming chunk contains observations for the classes that the binary learner treats as either positive or negative. Therefore, when the labels in incoming data are not well distributed for all expected classes, a good practice is to choose a coding design that does not have zeros in the coding matrix so that the software trains all binary learners for every chunk.
Create a new ECOC model for incremental learning. Specify the onevsall coding design. In this design, one class is positive and the rest are negative for each binary learner.
MdlLate = incrementalClassificationECOC(MaxNumClasses=5,Coding="onevsall")MdlLate =
incrementalClassificationECOC
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1×0 double]
ScoreTransform: 'none'
BinaryLearners: {5×1 cell}
CodingName: 'onevsall'
Decoding: 'lossweighted'
Properties, Methods
Display the coding design matrix.
MdlLate.CodingMatrix
ans = 5×5
1 -1 -1 -1 -1
-1 1 -1 -1 -1
-1 -1 1 -1 -1
-1 -1 -1 1 -1
-1 -1 -1 -1 1
Fit the incremental model and plot the results. Store the first model coefficients of the first and fifth binary learners, and .
mcnew = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); beta11new = zeros(nchunk,1); beta51new = zeros(nchunk,1); for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; MdlLate = updateMetricsAndFit(MdlLate,Xnew(idx,:),Ynew(idx)); mcnew{j,:} = MdlLate.Metrics{"ClassificationError",:}; beta11new(j) = MdlLate.BinaryLearners{1}.Beta(1); beta51new(j) = MdlLate.BinaryLearners{5}.Beta(1); end t = tiledlayout(3,1); nexttile plot(beta11new) xline(MdlLate.MetricsWarmupPeriod/numObsPerChunk,"--") xline((n-m)/numObsPerChunk,":") ylabel("\beta_{11}") xlim([0 nchunk]) nexttile plot(beta51new) xline(MdlLate.MetricsWarmupPeriod/numObsPerChunk,"--") xline((n-m)/numObsPerChunk,":") ylabel("\beta_{51}") xlim([0 nchunk]) nexttile plot(mcnew.Variables) xline(MdlLate.MetricsWarmupPeriod/numObsPerChunk,"--") xline((n-m)/numObsPerChunk,":") xlim([0 nchunk]) ylabel("Classification Error") legend(mcnew.Properties.VariableNames,Location="best") xlabel(t,"Iteration")

The updateMetricsAndFit function trains the model throughout incremental learning. However, does not change significantly until an incoming chunk contains observations with the fifth class (the dotted vertical line). Also, the function starts tracking performance metrics only after the model is fit to the expected number of classes.
Create an incremental ECOC model when you know all the class names in the data.
Consider training a device to predict whether a subject is sitting, standing, walking, running, or dancing based on biometric data measured on the subject. The class names map 1 through 5 to an activity.
Create an incremental ECOC model for multiclass learning. Specify the class names.
classnames = 1:5; Mdl = incrementalClassificationECOC(ClassNames=classnames)
Mdl =
incrementalClassificationECOC
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
Mdl is an incrementalClassificationECOC model object. All its properties are read-only.
Mdl must be fit to data before you can use it to perform any other operations.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Fit the incremental model to the training data by using the updateMetricsAndFit function. Simulate a data stream by processing chunks of 50 observations at a time. At each iteration:
Process 50 observations.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = updateMetricsAndFit(Mdl,X(idx,:),Y(idx)); end
In addition to specifying the maximum number of classes, prepare an incremental ECOC learner by specifying a metrics warm-up period and a metrics window size.
Load the human activity data set. Randomly shuffle the data. Orient the observations of the predictor data in columns.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:)'; Y = actid(idx);
For details on the data set, enter Description at the command line.
Create an incremental ECOC model for multiclass learning. Configure the model as follows:
Set the maximum number of classes to 5.
Specify a metrics warm-up period of 5000 observations.
Specify a metrics window size of 500 observations.
Mdl = incrementalClassificationECOC(MaxNumClasses=5, ...
MetricsWarmupPeriod=5000,MetricsWindowSize=500)Mdl =
incrementalClassificationECOC
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1×0 double]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
Mdl is an incrementalClassificationECOC model object configured for incremental learning. By default, incrementalClassificationECOC uses classification error loss to measure the performance of the model.
Fit the incremental model to the rest of the data by using the updateMetricsAndFit function. At each iteration:
Simulate a data stream by processing a chunk of 50 observations.
Overwrite the previous incremental model with a new one fitted to the incoming observations. Specify that the observations are oriented in columns.
Store the first model coefficient of the first binary learner , the cumulative metrics, and the window metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); ce = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); beta11 = zeros(nchunk,1); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = updateMetricsAndFit(Mdl,X(:,idx),Y(idx),ObservationsIn="columns"); ce{j,:} = Mdl.Metrics{"ClassificationError",:}; beta11(j) = Mdl.BinaryLearners{1}.Beta(1); end
Mdl is an incrementalClassificationECOC model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.
To see how the performance metrics and evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(beta11) ylabel("\beta_{11}") xlim([0 nchunk]) xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--") nexttile plot(ce.Variables) xlim([0 nchunk]) ylabel("Classification Error") xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--") legend(ce.Properties.VariableNames) xlabel(t,"Iteration")

The plots indicate that updateMetricsAndFit performs the following actions:
Fit during all incremental learning iterations.
Compute the performance metrics after the metrics warm-up period (dashed vertical line) only.
Compute the cumulative metrics during each iteration.
Compute the window metrics after processing 500 observations (10 iterations).
Train an ECOC model for multiclass classification by using fitcecoc. Then, convert the model to an incremental learner, track its performance, and fit the model to streaming data. Carry over training options from traditional to incremental learning.
Load and Preprocess Data
Load the human activity data set. Randomly shuffle the data.
load humanactivity rng(1) % For reproducibility n = numel(actid); idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Suppose that the data collected when the subject was stationary (Y <= 2) has double the quality than when the subject was moving. Create a weight variable that attributes 2 to observations collected from a stationary subject, and 1 to a moving subject.
W = ones(n,1) + (Y <= 2);
Train ECOC Model
Fit an ECOC model for multiclass classification to a random sample of half the data.
idxtt = randsample([true false],n,true); TTMdl = fitcecoc(X(idxtt,:),Y(idxtt),Weights=W(idxtt))
TTMdl =
ClassificationECOC
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Properties, Methods
TTMdl is a ClassificationECOC model object representing a traditionally trained ECOC model.
Convert Trained Model
Convert the traditionally trained ECOC model to a model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationECOC
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
IncrementalMdl is an incrementalClassificationECOC model object configured for incremental learning.
Separately Track Performance Metrics and Fit Model
Perform incremental learning on the rest of the data by using the updateMetrics and fit functions. Simulate a data stream by processing 50 observations at a time. At each iteration:
Call
updateMetricsto update the cumulative and window classification error of the model given the incoming chunk of observations. Overwrite the previous incremental model to update theMetricsproperty. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model. Specify the observation weights.Call
fitto fit the model to the incoming chunk of observations. Overwrite the previous incremental model to update the model parameters. Specify the observation weights.Store the classification error and first model coefficient of the first binary learner .
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 50; nchunk = floor(nil/numObsPerChunk); ec = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); beta11 = [IncrementalMdl.BinaryLearners{1}.Beta(1); zeros(nchunk+1,1)]; Xil = X(idxil,:); Yil = Y(idxil); Wil = W(idxil); % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx), ... Weights=Wil(idx)); ec{j,:} = IncrementalMdl.Metrics{"ClassificationError",:}; IncrementalMdl = fit(IncrementalMdl,Xil(idx,:),Yil(idx),Weights=Wil(idx)); beta11(j+1) = IncrementalMdl.BinaryLearners{1}.Beta(1); end
IncrementalMdl is an incrementalClassificationECOC model object trained on all the data in the stream.
Alternatively, you can use updateMetricsAndFit to update the performance metrics of the model given a new chunk of data, and then fit the model to the data.
Plot a trace plot of the performance metrics and estimated coefficient on separate tiles.
t = tiledlayout(2,1); nexttile plot(ec.Variables) xlim([0 nchunk]) ylabel("Classification Error") legend(ec.Properties.VariableNames) nexttile plot(beta11) ylabel("\beta_{11}") xlim([0 nchunk]) xlabel(t,"Iteration")
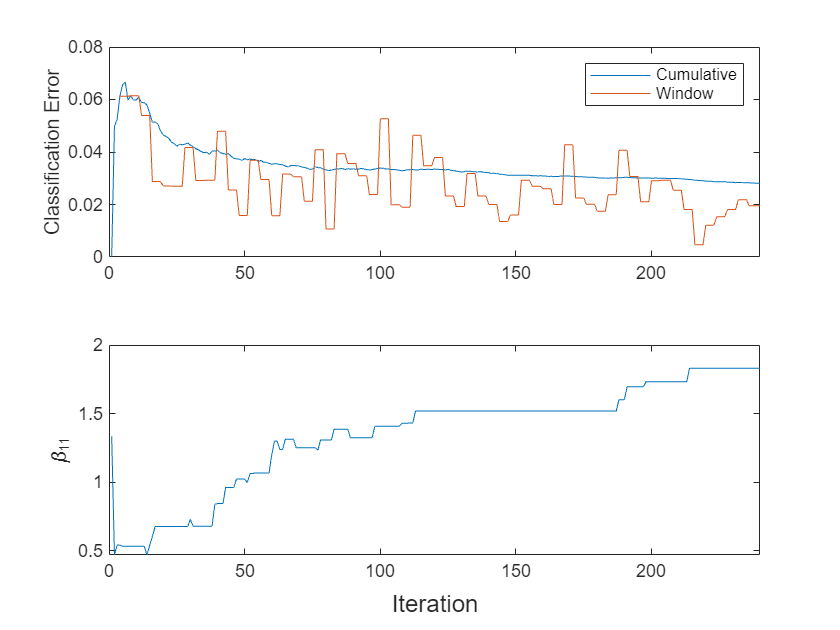
The cumulative loss levels quickly and is stable, whereas the window loss jumps throughout the training.
changes abruptly at first, then gradually levels off as fit processes more chunks.
Customize binary learners of an incrementalClassificationECOC model object by specifying the Learners name-value argument.
First, configure binary learner properties by creating an incrementalClassificationLinear object. Set the linear classification model type (Learner) to logistic regression, and specify Standardize as true to standardize the predictor data.
binaryMdl = incrementalClassificationLinear(Learner="logistic", ... Standardize=true)
binaryMdl =
incrementalClassificationLinear
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1×0 double]
ScoreTransform: 'logit'
Beta: [0×1 double]
Bias: 0
Learner: 'logistic'
Properties, Methods
Create an incremental ECOC model for multiclass learning. Specify the number of classes in the data as five, and set the binary learner template (Learners) to binaryMdl.
Mdl = incrementalClassificationECOC(MaxNumClasses=5,Learners=binaryMdl)
Mdl =
incrementalClassificationECOC
IsWarm: 0
Metrics: [1×2 table]
ClassNames: [1×0 double]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
Display the BinaryLearners property in Mdl.
Mdl.BinaryLearners
ans=10×1 cell array
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
{1×1 incrementalClassificationLinear}
By default, incrementalClassificationECOC uses the one-versus-one coding design, which requires 10 learners for five classes. Therefore, the BinaryLearners property contains 10 binary learners of type incrementalClassificationLinear.
More About
Incremental learning, or online learning, is a branch of machine learning concerned with processing incoming data from a data stream, possibly given little to no knowledge of the distribution of the predictor variables, aspects of the prediction or objective function (including tuning parameter values), or whether the observations are labeled. Incremental learning differs from traditional machine learning, where enough labeled data is available to fit to a model, perform cross-validation to tune hyperparameters, and infer the predictor distribution.
Given incoming observations, an incremental learning model processes data in any of the following ways, but usually in this order:
Predict labels.
Measure the predictive performance.
Check for structural breaks or drift in the model.
Fit the model to the incoming observations.
For more details, see Incremental Learning Overview.
The adaptive scale-invariant solver for incremental learning, introduced in [5], is a gradient-descent-based objective solver for training linear predictive models. The solver is hyperparameter free, insensitive to differences in predictor variable scales, and does not require prior knowledge of the distribution of the predictor variables. These characteristics make it well suited to incremental learning.
The incremental fitting functions fit and updateMetricsAndFit use the more aggressive ScInOL2 version of the algorithm
to train binary learners. The functions always shuffles an incoming batch of data before
fitting the model.
An error-correcting output codes (ECOC) model reduces the problem of classification with three or more classes to a set of binary classification problems.
ECOC classification requires a coding design, which determines the classes that the binary learners train on, and a decoding scheme, which determines how the results (predictions) of the binary classifiers are aggregated.
Assume the following:
The classification problem has three classes.
The coding design is one-versus-one. For three classes, this coding design is
You can specify a different coding design by using the
Codingname-value argument when you create a classification model.The model determines the predicted class by using the loss-weighted decoding scheme with the binary loss function g. The software also supports the loss-based decoding scheme. You can specify the decoding scheme and binary loss function by using the
DecodingandBinaryLossname-value arguments, respectively, when you create a classification model or when you call the object functionspredictandloss.
To build this classification model, the ECOC algorithm follows these steps.
Learner 1 trains on observations in Class 1 or Class 2, and treats Class 1 as the positive class and Class 2 as the negative class. The other learners are trained similarly.
Let M be the coding design matrix with elements mkl, and sl be the predicted classification score for the positive class of learner l. The algorithm assigns a new observation to the class () that minimizes the aggregation of the losses for the L binary learners.
ECOC models can improve classification accuracy, compared to other multiclass models [4].
The coding design is a matrix whose elements direct which classes are trained by each binary learner, that is, how the multiclass problem is reduced to a series of binary problems.
Each row of the coding design corresponds to a distinct class, and each column corresponds to a binary learner. In a ternary coding design, for a particular column (or binary learner):
A row containing 1 directs the binary learner to group all observations in the corresponding class into a positive class.
A row containing –1 directs the binary learner to group all observations in the corresponding class into a negative class.
A row containing 0 directs the binary learner to ignore all observations in the corresponding class.
Coding design matrices with large, minimal, pairwise row distances based on the Hamming measure are optimal. For details on the pairwise row distance, see Random Coding Design Matrices and [3].
This table describes popular coding designs.
| Coding Design | Description | Number of Learners | Minimal Pairwise Row Distance |
|---|---|---|---|
| one-versus-all (OVA) | For each binary learner, one class is positive and the rest are negative. This design exhausts all combinations of positive class assignments. | K | 2 |
| one-versus-one (OVO) | For each binary learner, one class is positive, one class is negative, and the rest are ignored. This design exhausts all combinations of class pair assignments. | K(K – 1)/2 | 1 |
| binary complete | This design partitions the classes into all binary
combinations, and does not ignore any classes. That is, all class
assignments are | 2K – 1 – 1 | 2K – 2 |
| ternary complete | This design partitions the classes into all ternary
combinations. That is, all class assignments are
| (3K – 2K + 1 + 1)/2 | 3K – 2 |
| ordinal | For the first binary learner, the first class is negative and the rest are positive. For the second binary learner, the first two classes are negative and the rest are positive, and so on. | K – 1 | 1 |
| dense random | For each binary learner, the software randomly assigns classes into positive or negative classes, with at least one of each type. For more details, see Random Coding Design Matrices. | Random, but approximately 10 log2K | Variable |
| sparse random | For each binary learner, the software randomly assigns classes as positive or negative with probability 0.25 for each, and ignores classes with probability 0.5. For more details, see Random Coding Design Matrices. | Random, but approximately 15 log2K | Variable |
This plot compares the number of binary learners for the coding designs with an increasing number of classes (K).

The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.
Assume the following:
mkj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.
sj is the score of binary learner j for an observation.
g is the binary loss function.
is the predicted class for the observation.
The software supports two decoding schemes:
Loss-based decoding [3] (
Decodingis"lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.Loss-weighted decoding [2] (
Decodingis"lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.
The predict, resubPredict, and
kfoldPredict functions return the negated value of the objective
function of argmin as the second output argument
(NegLoss) for each observation and class.
This table summarizes the supported binary loss functions, where yj is a class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss function.
| Value | Description | Score Domain | g(yj,sj) |
|---|---|---|---|
"binodeviance" | Binomial deviance | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | Exponential | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | Hamming | [0,1] or (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | Hinge | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | Linear | (–∞,∞) | (1 – yjsj)/2 |
"logit" | Logistic | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | Quadratic | [0,1] | [1 – yj(2sj – 1)]2/2 |
The software normalizes binary losses so that the loss is 0.5 when yj = 0, and aggregates using the average of the binary learners [1].
Do not confuse the binary loss with the overall classification loss (specified by the
LossFun name-value argument of the loss and
predict object functions), which measures how well an ECOC classifier
performs as a whole.
The classification error has the form
where:
wj is the weight for observation j. The software renormalizes the weights to sum to 1.
ej = 1 if the predicted class of observation j differs from its true class, and 0 otherwise.
In other words, the classification error is the proportion of observations misclassified by the classifier.
Algorithms
The
updateMetricsandupdateMetricsAndFitfunctions track model performance metrics (Metrics) from new data only when the incremental model is warm (IsWarmproperty istrue).If you create an incremental model by using
incrementalLearnerandMetricsWarmupPeriodis 0 (default forincrementalLearner), the model is warm at creation.Otherwise, an incremental model becomes warm after
fitorupdateMetricsAndFitperforms both of these actions:Fit the incremental model to
MetricsWarmupPeriodobservations, which is the metrics warm-up period.Fit the incremental model to all expected classes (see the
MaxNumClassesandClassNamesarguments ofincrementalClassificationECOC).
The
Metricsproperty of the incremental model stores two forms of each performance metric as variables (columns) of a table,CumulativeandWindow, with individual metrics in rows. When the incremental model is warm,updateMetricsandupdateMetricsAndFitupdate the metrics at the following frequencies:Cumulative— The functions compute cumulative metrics since the start of model performance tracking. The functions update metrics every time you call the functions and base the calculation on the entire supplied data set.Window— The functions compute metrics based on all observations within a window determined byMetricsWindowSize, which also determines the frequency at which the software updatesWindowmetrics. For example, ifMetricsWindowSizeis 20, the functions compute metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store a buffer of length
MetricsWindowSizefor each specified metric, and store a buffer of observation weights.Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.
When the buffer is full, overwrite the
Windowfield of theMetricsproperty with the weighted average performance in the metrics window. If the buffer overfills when the function processes a batch of observations, the latest incomingMetricsWindowSizeobservations enter the buffer, and the earliest observations are removed from the buffer. For example, supposeMetricsWindowSizeis 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the functions use the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a
NaNscore when computing theCumulativeandWindowperformance metric values.
Custom coding matrices must have a certain form. The software validates a custom coding matrix by ensuring:
Every element is –1, 0, or 1.
Every column contains as least one –1 and one 1.
For all distinct column vectors u and v, u ≠ v and u ≠ –v.
All row vectors are unique.
The matrix can separate any two classes. That is, you can move from any row to any other row following these rules:
Move vertically from 1 to –1 or –1 to 1.
Move horizontally from a nonzero element to another nonzero element.
Use a column of the matrix for a vertical move only once.
If it is not possible to move from row i to row j using these rules, then classes i and j cannot be separated by the design. For example, in the coding design
classes 1 and 2 cannot be separated from classes 3 and 4 (that is, you cannot move horizontally from –1 in row 2 to column 2 because that position contains a 0). Therefore, the software rejects this coding design.
For a given number of classes K, the software generates random coding design matrices as follows.
The software generates one of these matrices:
Dense random — The software assigns 1 or –1 with equal probability to each element of the K-by-Ld coding design matrix, where .
Sparse random — The software assigns 1 to each element of the K-by-Ls coding design matrix with probability 0.25, –1 with probability 0.25, and 0 with probability 0.5, where .
If a column does not contain at least one 1 and one –1, then the software removes that column.
For distinct columns u and v, if u = v or u = –v, then the software removes v from the coding design matrix.
The software randomly generates 10,000 matrices by default, and retains the matrix with the largest, minimal, pairwise row distance based on the Hamming measure ([3]) given by
where mkjl is an element of coding design matrix j.
References
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
[3] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
[4] Fürnkranz, Johannes. “Round Robin Classification.” J. Mach. Learn. Res., Vol. 2, 2002, pp. 721–747.
[5] Kempka, Michał, Wojciech Kotłowski, and Manfred K. Warmuth. "Adaptive Scale-Invariant Online Algorithms for Learning Linear Models." Preprint, submitted February 10, 2019. https://arxiv.org/abs/1902.07528.
Extended Capabilities
Usage notes and limitations:
The
fit,loss,predict,updateMetrics, andupdateMetricsAndFitfunctions support code generation.When you create an
incrementalClassificationECOCmodel object, the following restrictions apply.You must specify
ClassNamesandNumPredictors.The binary learners must be linear.
When you generate code that loads or creates an
incrementalClassificationECOCmodel object, the following restrictions apply.The number of predictor variables must equal
Mdl.NumPredictors.The
ClassNamesproperty must contain all expected class names.
For more information, see Introduction to Code Generation.
Version History
Introduced in R2022a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)