loss
Description
loss returns the regression or classification loss of
a configured incremental learning model for kernel regression (incrementalRegressionKernel object) or binary kernel classification (incrementalClassificationKernel object).
To measure model performance on a data stream and store the results in the output model,
call updateMetrics or
updateMetricsAndFit.
Examples
The performance of an incremental model on streaming data is measured in three ways:
Cumulative metrics measure the performance since the start of incremental learning.
Window metrics measure the performance on a specified window of observations. The metrics are updated every time the model processes the specified window.
The
lossfunction measures the performance on a specified batch of data only.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Responses can be one of five classes: Sitting, Standing, Walking, Running, or Dancing. Dichotomize the response by identifying whether the subject is moving (actid > 2).
Y = Y > 2;
Create an incremental kernel model for binary classification. Specify a metrics window size of 1000 observations. Configure the model for loss by fitting it to the first 10 observations.
p = size(X,2); Mdl = incrementalClassificationKernel(MetricsWindowSize=1000); initobs = 10; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
Mdl is an incrementalClassificationKernel model. All its properties are read-only.
Simulate a data stream, and perform the following actions on each incoming chunk of 50 observations:
Call
updateMetricsto measure the cumulative performance and the performance within a window of observations. Overwrite the previous incremental model with a new one to track performance metrics.Call
lossto measure the model performance on the incoming chunk.Call
fitto fit the model to the incoming chunk. Overwrite the previous incremental model with a new one fitted to the incoming observations.Store all performance metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor((n - initobs)/numObsPerChunk); ce = array2table(zeros(nchunk,3),VariableNames=["Cumulative","Window","Loss"]); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); ce{j,["Cumulative","Window"]} = Mdl.Metrics{"ClassificationError",:}; ce{j,"Loss"} = loss(Mdl,X(idx,:),Y(idx)); Mdl = fit(Mdl,X(idx,:),Y(idx)); end
Mdl is an incrementalClassificationKernel model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetrics checks the performance of the model on the incoming observations, and the fit function fits the model to those observations. loss is agnostic of the metrics warm-up period, so it measures the classification error for all iterations.
To see how the performance metrics evolve during training, plot them.
plot(ce.Variables) xlim([0 nchunk]) ylabel("Classification Error") xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--") legend(ce.Properties.VariableNames) xlabel("Iteration")
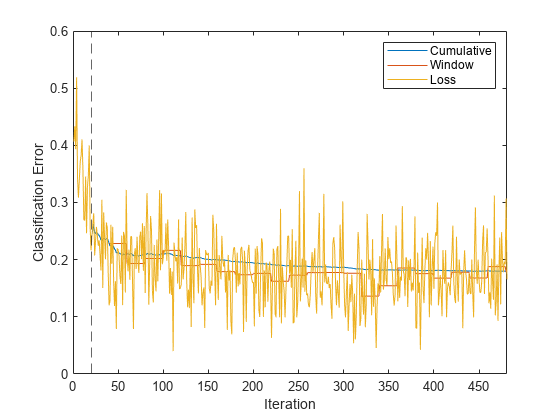
The yellow line represents the classification error on each incoming chunk of data. After the metrics warm-up period, Mdl tracks the cumulative and window metrics. The cumulative and batch losses converge as the fit function fits the incremental model to the incoming data.
Fit an incremental learning model for regression to streaming data, and compute the mean absolute deviation (MAD) on the incoming data batches.
Load the robot arm data set. Obtain the sample size n and the number of predictor variables p.
load robotarm
n = numel(ytrain);
p = size(Xtrain,2);For details on the data set, enter Description at the command line.
Create an incremental kernel model for regression. Configure the model as follows:
Specify a metrics warm-up period of 1000 observations.
Specify a metrics window size of 500 observations.
Track the mean absolute deviation (MAD) to measure the performance of the model. Create an anonymous function that measures the absolute error of each new observation. Create a structure array containing the name
MeanAbsoluteErrorand its corresponding function.Configure the model to predict responses by fitting it to the first 10 observations.
maefcn = @(z,zfit,w)(abs(z - zfit));
maemetric = struct(MeanAbsoluteError=maefcn);
Mdl = incrementalRegressionKernel(MetricsWarmupPeriod=1000,MetricsWindowSize=500, ...
Metrics=maemetric);
initobs = 10;
Mdl = fit(Mdl,Xtrain(1:initobs,:),ytrain(1:initobs));Mdl is an incrementalRegressionKernel model object configured for incremental learning.
Perform incremental learning. At each iteration:
Simulate a data stream by processing a chunk of 50 observations.
Call
updateMetricsto compute cumulative and window metrics on the incoming chunk of data. Overwrite the previous incremental model with a new one fitted to overwrite the previous metrics.Call
lossto compute the MAD on the incoming chunk of data. Whereas the cumulative and window metrics require that custom losses return the loss for each observation,lossrequires the loss on the entire chunk. Compute the mean of the absolute deviation.Call
fitto fit the incremental model to the incoming chunk of data.Store the cumulative, window, and chunk metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor((n - initobs)/numObsPerChunk); mae = array2table(zeros(nchunk,3),VariableNames=["Cumulative","Window","Chunk"]); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,Xtrain(idx,:),ytrain(idx)); mae{j,1:2} = Mdl.Metrics{"MeanAbsoluteError",:}; mae{j,3} = loss(Mdl,Xtrain(idx,:),ytrain(idx),LossFun=@(x,y,w)mean(maefcn(x,y,w))); Mdl = fit(Mdl,Xtrain(idx,:),ytrain(idx)); end
Mdl is an incrementalRegressionKernel model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetrics checks the performance of the model on the incoming observations, and the fit function fits the model to those observations.
Plot the performance metrics to see how they evolved during incremental learning.
plot(mae.Variables) ylabel("Mean Absolute Deviation") xlabel("Iteration") xlim([0 nchunk]) xline(Mdl.EstimationPeriod/numObsPerChunk,"-.") xline((Mdl.EstimationPeriod + Mdl.MetricsWarmupPeriod)/numObsPerChunk,"--") legend(mae.Properties.VariableNames)

The plot suggests the following:
updateMetricscomputes the performance metrics after the metrics warm-up period only.updateMetricscomputes the cumulative metrics during each iteration.updateMetricscomputes the window metrics after processing 500 observations (10 iterations).Because
Mdlwas configured to predict observations from the beginning of incremental learning,losscan compute the MAD on each incoming chunk of data.
Input Arguments
Incremental learning model, specified as an incrementalClassificationKernel or incrementalRegressionKernel model object. You can create Mdl directly or by converting a supported, traditionally trained machine learning model using the incrementalLearner function. For more details, see the corresponding reference page.
You must configure Mdl to predict labels for a batch of observations.
If
Mdlis a converted, traditionally trained model, you can predict labels without any modifications.Otherwise, you must fit
Mdlto data usingfitorupdateMetricsAndFit.
Batch of predictor data, specified as a floating-point matrix of
n observations and Mdl.NumPredictors predictor
variables.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row) in j)X.
Note
loss supports only floating-point
input predictor data. If your input data includes categorical data, you must prepare an encoded
version of the categorical data. Use dummyvar to convert each categorical variable
to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any
other numeric predictors. For more details, see Dummy Variables.
Data Types: single | double
Batch of responses (labels), specified as a categorical, character, or string array, a logical or floating-point vector, or a cell array of character vectors for classification problems; or a floating-point vector for regression problems.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row) in j)X.
For classification problems:
losssupports binary classification only.If
Ycontains a label that is not a member ofMdl.ClassNames,lossissues an error.The data type of
YandMdl.ClassNamesmust be the same.
Data Types: char | string | cell | categorical | logical | single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: LossFun="epsiloninsensitive",Weights=W returns the epsilon
insensitive loss and specifies the observation weights as the vector
W.
Loss function, specified as a built-in loss function name or function handle.
Classification problems: The following table lists the available loss functions when
Mdlis anincrementalClassificationKernelmodel. Specify one using its corresponding character vector or string scalar.Name Description "binodeviance"Binomial deviance "classiferror"(default)Misclassification rate in decimal "exponential"Exponential loss "hinge"Hinge loss "logit"Logistic loss "quadratic"Quadratic loss For more details, see Classification Loss.
Logistic regression learners return posterior probabilities as classification scores, but SVM learners do not (see
predict).To specify a custom loss function, use function handle notation. The function must have this form:
lossval = lossfcn(C,S,W)
The output argument
lossvalis an n-by-1 floating-point vector, wherelossval(is the classification loss of observationj)jYou specify the function name (
lossfcnCis an n-by-2 logical matrix with rows indicating the class to which the corresponding observation belongs. The column order corresponds to the class order in theClassNamesproperty. CreateCby settingC(=p,q)1, if observationpqp0.Sis an n-by-2 numeric matrix of predicted classification scores.Sis similar to thescoreoutput ofpredict, where rows correspond to observations in the data and the column order corresponds to the class order in theClassNamesproperty.S(is the classification score of observationp,q)pqWis an n-by-1 numeric vector of observation weights.
Regression problems: The following table lists the available loss functions when
Mdlis anincrementalRegressionKernelmodel. Specify one using its corresponding character vector or string scalar.Name Description Learner Supporting Metric "epsiloninsensitive"Epsilon insensitive loss 'svm'"mse"(default)Weighted mean squared error 'svm'and'leastsquares'For more details, see Regression Loss.
To specify a custom loss function, use function handle notation. The function must have this form:
lossval = lossfcn(Y,YFit,W)
The output argument
lossvalis a floating-point scalar.You specify the function name (
lossfcnYis a length n numeric vector of observed responses.YFitis a length n numeric vector of corresponding predicted responses.Wis an n-by-1 numeric vector of observation weights.
Example: LossFun="mse"
Example: LossFun=@lossfcn
Data Types: char | string | function_handle
Batch of observation weights, specified as a floating-point vector of positive values. loss weighs the observations in the input data with the corresponding values in Weights. The size of Weights must equal n, which is the number of observations in the input data.
By default, Weights is ones(.n,1)
For more details, see Observation Weights.
Example: Weights=W specifies the observation weights as the vector
W.
Data Types: double | single
Output Arguments
More About
Classification loss functions measure the predictive inaccuracy of classification models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.
Consider the following scenario.
L is the weighted average classification loss.
n is the sample size.
yj is the observed class label. The software codes it as –1 or 1, indicating the negative or positive class (or the first or second class in the
ClassNamesproperty), respectively.f(Xj) is the positive-class classification score for observation (row) j of the predictor data X.
mj = yjf(Xj) is the classification score for classifying observation j into the class corresponding to yj. Positive values of mj indicate correct classification and do not contribute much to the average loss. Negative values of mj indicate incorrect classification and contribute significantly to the average loss.
The weight for observation j is wj.
Given this scenario, the following table describes the supported loss functions that you
can specify by using the LossFun name-value argument.
| Loss Function | Value of LossFun | Equation |
|---|---|---|
| Binomial deviance | "binodeviance" | |
| Exponential loss | "exponential" | |
| Misclassification rate in decimal | "classiferror" | where is the class label corresponding to the class with the maximal score, and I{·} is the indicator function. |
| Hinge loss | "hinge" | |
| Logistic loss | "logit" | |
| Quadratic loss | "quadratic" |
The loss function does not omit an observation with a
NaN score when computing the weighted average loss. Therefore,
loss can return NaN when the predictor
data X contains missing values, and the name-value argument
LossFun is not specified as "classiferror". In
most cases, if the data set does not contain missing predictors, the
loss function does not return NaN.
This figure compares the loss functions over the score m for one observation. Some functions are normalized to pass through the point (0,1).

Regression loss functions measure the predictive inaccuracy of regression models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.
Consider the following scenario.
L is the weighted average classification loss.
n is the sample size.
yj is the observed response of observation j.
f(Xj) is the predicted value of observation j of the predictor data X.
The weight for observation j is wj.
Given this scenario, the following table describes the supported loss functions that you can specify by using the LossFun name-value argument.
| Loss Function | Value of LossFun | Equation |
|---|---|---|
| Epsilon insensitive loss | "epsiloninsensitive" | |
| Mean squared error | "mse" |
The loss function does not omit an observation with a
NaN prediction when computing the weighted average loss. Therefore,
loss can return NaN when the predictor
data X contains missing values. In most cases, if the data set does not
contain missing predictors, the loss function does not return
NaN.
Algorithms
For classification problems, if the prior class probability distribution is known (in other words, the prior distribution is not empirical), loss normalizes observation weights to sum to the prior class probabilities in the respective classes. This action implies that observation weights are the respective prior class probabilities by default.
For regression problems or if the prior class probability distribution is empirical, the software normalizes the specified observation weights to sum to 1 each time you call loss.
Version History
Introduced in R2022a
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)