plotInteraction

Plot interaction effects of two predictors in linear regression model

Syntax

plotInteraction(mdl,var1,var2)

plotInteraction(mdl,var1,var2,ptype)

plotInteraction(ax,___)

h = plotInteraction(___)

Description

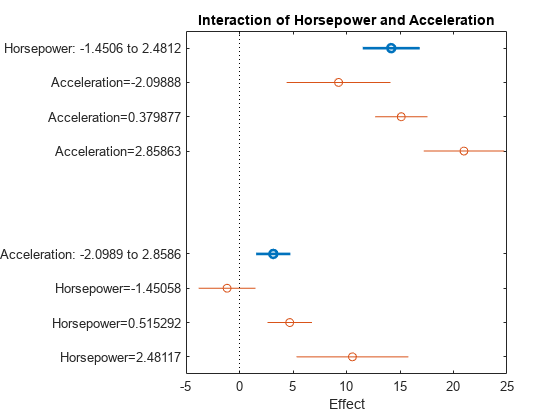
plotInteraction(mdl,var1,var2) creates a plot of the main effects of the two selected predictors var1 and var2 and their conditional effects in the linear regression model mdl. Horizontal lines through the effect values indicate their 95% confidence intervals.

plotInteraction(mdl,var1,var2,ptype) specifies the plot type ptype. For example, if ptype is 'predictions', then plotInteraction plots the adjusted response function as a function of the second predictor, with the first predictor fixed at specific values. For details, see Conditional Effect.

plotInteraction(ax,___) plots into the axes specified by ax instead of the current axes (gca) using any of the input argument combinations in the previous syntaxes. Alternatively, you can specify Parent=ax as the last input argument. (since R2024a)

h = plotInteraction(___) returns a vector of line objects h. Use h to modify the properties of a specific line after you create the plot. For a list of properties, see Line Properties.

Examples

Interaction Plot of Main Effects and Conditional Effects

Fit a model with an interaction term and create an interaction plot that shows the main effects and conditional effects.

Using the data in the carsmall data set, create response values that include an interaction term. First, load the data set and normalize the predictor data.

load carsmall
Acceleration = normalize(Acceleration); 
Horsepower = normalize(Horsepower);
Displacement = normalize(Displacement);

Define a response variable that includes the interaction term Acceleration*Horsepower.

y = Acceleration + 4*Horsepower + Acceleration.*Horsepower + Displacement;

Add some noise to the response values.

rng('default') % For reproducibility
y = y + normrnd(10,0.25*std(y,'omitnan'),size(y));

Create a table that includes the predictor data and response values.

tbl = table(Acceleration,Horsepower,Displacement,y);

Fit a linear regression model.

mdl = fitlm(tbl,'y ~ Acceleration + Horsepower + Acceleration*Horsepower + Displacement + Horsepower*Displacement')

mdl = 
Linear regression model:
    y ~ 1 + Acceleration*Horsepower + Horsepower*Displacement

Estimated Coefficients:
                                Estimate       SE         tStat        pValue  
                               __________    _______    _________    __________

    (Intercept)                    9.8652    0.16177       60.982     8.587e-77
    Acceleration                  0.63726     0.1626       3.9191    0.00016967
    Horsepower                     3.6168       0.34       10.638     9.273e-18
    Displacement                  0.95032    0.31828       2.9858     0.0036144
    Acceleration:Horsepower       0.60108     0.1851       3.2473     0.0016209
    Horsepower:Displacement    -0.0096069    0.20947    -0.045863       0.96352


Number of observations: 99, Error degrees of freedom: 93
Root Mean Squared Error: 1.07
R-squared: 0.93,  Adjusted R-Squared: 0.927
F-statistic vs. constant model: 249, p-value = 3.3e-52

pValue of the interaction term Acceleration*Horsepower is very small, meaning that the interaction term is statistically significant.

Create an interaction plot that shows the main effects and conditional effects of Horsepower and Acceleration.

plotInteraction(mdl,'Horsepower','Acceleration')

For each predictor, the main effect point and its conditional effect points are not vertically aligned. Therefore, you cannot find any vertical lines that pass through the confidence intervals of the main and conditional effect points for each predictor. This plot indicates the existence of interaction effects on the response variable.

For comparison, create an interaction plot for Displacement and Horsepower. This p-value of this interaction term (Displacement*Horsepower) is large, meaning that the interaction term is not statistically significant.

plotInteraction(mdl,'Displacement','Horsepower')

For each predictor, the main effect point and its conditional effect points are aligned vertically. This plot indicates no interaction.

Interaction Plot of Adjusted Response Curve

Fit a model with an interaction term and create an interaction plot of adjusted response curves.

Using the data in the carsmall data set, create response values that include an interaction term. First, load the data set and normalize the predictor data.

load carsmall
Acceleration = normalize(Acceleration); 
Horsepower = normalize(Horsepower);
Displacement = normalize(Displacement);

Define a response variable that includes the interaction term Acceleration*Horsepower.

y = Acceleration + 4*Horsepower + Acceleration.*Horsepower + Displacement;

Add some noise to the response values.

rng('default') % For reproducibility
y = y + normrnd(10,0.25*std(y,'omitnan'),size(y));

Create a table that includes the predictor data and response values.

tbl = table(Acceleration,Horsepower,Displacement,y);

Fit a linear regression model.

mdl = fitlm(tbl,'y ~ Acceleration + Horsepower + Acceleration*Horsepower + Displacement + Horsepower*Displacement')

mdl = 
Linear regression model:
    y ~ 1 + Acceleration*Horsepower + Horsepower*Displacement

Estimated Coefficients:
                                Estimate       SE         tStat        pValue  
                               __________    _______    _________    __________

    (Intercept)                    9.8652    0.16177       60.982     8.587e-77
    Acceleration                  0.63726     0.1626       3.9191    0.00016967
    Horsepower                     3.6168       0.34       10.638     9.273e-18
    Displacement                  0.95032    0.31828       2.9858     0.0036144
    Acceleration:Horsepower       0.60108     0.1851       3.2473     0.0016209
    Horsepower:Displacement    -0.0096069    0.20947    -0.045863       0.96352


Number of observations: 99, Error degrees of freedom: 93
Root Mean Squared Error: 1.07
R-squared: 0.93,  Adjusted R-Squared: 0.927
F-statistic vs. constant model: 249, p-value = 3.3e-52

pValue of the interaction term Acceleration*Horsepower is very small, meaning that the interaction term is statistically significant.

Create an interaction plot that shows the adjusted response function as a function of Acceleration, with Horsepower fixed at specific values.

plotInteraction(mdl,'Horsepower','Acceleration','predictions')

The curves are not parallel. This plot indicates interactions between the predictors.

For comparison, create an interaction plot for the Displacement and Horsepower. The p-value of this interaction term (Displacement*Horsepower) is large, meaning that the interaction term is not statistically significant.

plotInteraction(mdl,'Displacement','Horsepower','predictions')

The curves are parallel, indicating no interaction.

Input Arguments

mdl — Linear regression model object

LinearModel object | CompactLinearModel object

Linear regression model object, specified as a LinearModel object created by using fitlm or stepwiselm, or a CompactLinearModel object created by using compact.

var1 — First variable for plot

character vector | string array | positive integer

First variable for the plot, specified as a character vector or string array of the variable name in mdl.VariableNames (VariableNames property of mdl), or a positive integer representing the index of a variable in mdl.VariableNames.

Data Types: char | string | single | double

var2 — Second variable for plot

character vector | string array | positive integer

Second variable for the plot, specified as a character vector or string array of the variable name in mdl.VariableNames (VariableNames property of mdl), or a positive integer representing the index of a variable in mdl.VariableNames.

Data Types: char | string | single | double

ptype — Plot type

'effects' (default) | 'predictions'

Plot type, specified as one of these values:

• 'effects' — plotInteraction creates a plot of the main effects of the two selected predictors var1 and var2 and their conditional effects. Horizontal lines through the effect values indicate their 95% confidence intervals.

• 'predictions' — plotInteraction plots the adjusted response function as a function of var2, with var1 fixed at specific values.

For details, see Main Effect and Conditional Effect.

ax — Target axes

Axes object

Since R2024a

Target axes, specified as an Axes object. If you do not specify the axes, then plotInteraction uses the current axes (gca).

Output Arguments

h — Line objects

vector

Line objects, returned as a vector. Use dot notation to query and set properties of the line objects. For details, see Line Properties.

If the plot type is 'effects' (default), h(1) corresponds to the circles that represent the main effect estimates, and h(2) and h(3) correspond to the 95% confidence intervals for the two main effects. The remaining entries in h correspond to the conditional effects and their confidence intervals. The line objects associated with the main effects have the tag 'main'. The line objects associated with the conditional effects of var1 and var2 have the tags 'conditional1' and 'conditional2', respectively.

If the plot type is 'predictions', each entry in h corresponds to each curve on the plot.

More About

Main Effect

An effect, or main effect, of a predictor represents an effect of one predictor on the response from changing the predictor value while averaging out the effects of the other predictors.

For a predictor variable x_s, the effect is defined by

g(x_si) – g(x_sj) ,

where g is an Adjusted Response function. The plotEffects function chooses the observations i and j as follows. For a categorical variable that is not ordinal, x_si and x_sj are the predictor values that produce the maximum and minimum adjusted responses, respectively, so that the effect value is always positive. For a numeric variable or an ordinal categorical variable, the function chooses two predictor values that produce the minimum and maximum adjusted responses where x_si < x_sj.

plotEffects plots the effect value and the 95% confidence interval of the effect value for each predictor variable.

Adjusted Response

An adjusted response function describes the relationship between the fitted response and a single predictor, with the other predictors averaged out by averaging the fitted values over the data used in the fit.

A regression model for the predictor variables (x₁, x₂, …, x_p) and the response variable y has the form

y_i = f(x_1i, x_2i, …, x_pi) + r_i,

where f is a fitted regression function and r is a residual. The subscript i represents the observation number.

The adjusted response function for the first predictor variable x₁, for example, is defined as

$$g\left(x_1\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f\left(x_1,x_{2i},x_{3i},\mathrm{...},x_{pi}\right)},$$

where n is the number of observations. The adjusted response data value is the sum of the adjusted fitted value and the residual for each observation.

$${\tilde{y}}_i=g\left(x_{1i}\right)+r_i.$$

plotAdjustedResponse plots the adjusted response function and the adjusted response data values for a selected predictor variable.

Conditional Effect

When a model contains an interaction term, the main effect of one predictor depends on the value of another predictor that interacts with it. In this case, a conditional effect of one predictor given a specific value of another is helpful in understanding the actual effect of both predictors. You can examine whether the effect of one predictor depends on the value of another by using conditional effect values.

To define a conditional effect, define the adjusted response function as a function of two predictor variables. For example, the adjusted response function of x₁ and x₂ is

$$h\left(x_1,x_2\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}f\left(x_1,x_2,x_{3i},\mathrm{...},x_{pi}\right)},$$

where f is a fitted regression function, and n is the number of observations.

The conditional effect of one predictor (x₂) given a specific value of another predictor (x_1k) is defined by

h(x_1k,x_2i) - h(x_1k,x_2j).

To compute conditional effect values, plotInteraction chooses the observations i and j of x₂ in the same way as when the function computes the Main Effect and chooses the x_1k values. If x₁ is a categorical variable, then plotInteraction computes the conditional effect for all levels of x₁. If x₁ is a numeric variable, then plotInteraction computes the conditional effect for three values of x₁: the minimum value of x₁, the maximum value of x₁, and the average value of the minimum and maximum.

If the plot type is 'effects' (default), plotInteraction plots the main effects of the two selected predictors, their conditional effects, and the 95% confidence bounds for the effect values.

If the plot type is 'predictions', plotInteraction plots the adjusted response function as a function of the second predictor, with the first predictor fixed at specific values. For example, plotInteraction(mdl,'x1','x2','predictions') plots the curve of h(x_1k, x₂) for each x_1k value.

Tips

• The data cursor displays the values of the selected plot point in a data tip (small text box located next to the data point). The data tip includes the x-axis and y-axis values for the selected point, along with the observation name or number.

Alternative Functionality

• A LinearModel object provides multiple plotting functions.

  • When creating a model, use plotAdded to understand the effect of adding or removing a predictor variable.

  • When verifying a model, use plotDiagnostics to find questionable data and to understand the effect of each observation. Also, use plotResiduals to analyze the residuals of the model.

  • After fitting a model, use plotAdjustedResponse, plotPartialDependence, and plotEffects to understand the effect of a particular predictor. Use plotInteraction to understand the interaction effect between two predictors. Also, use plotSlice to plot slices through the prediction surface.

Extended Capabilities

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2012a

R2024a: Specify target axes

Specify the target axes for the plot by using the ax input argument or Parent=ax name-value argument.