Simulate the Motion of the Periodic Swing of a Pendulum

Step 1: Derive the Equation of Motion

The pendulum is a simple mechanical system that follows a differential equation. The pendulum is initially at rest in a vertical position. When the pendulum is displaced by an angle $$\theta$$ and released, the force of gravity pulls it back towards its resting position. Its momentum causes it to overshoot and come to an angle $$-\theta$$ (if there are no frictional forces), and so on. The restoring force along the motion of the pendulum due to gravity is $$-mg\sin \theta$$. Thus, according to Newton's second law, the mass times the acceleration must equal $$-mg\sin \theta$$.

syms m a g theta(t)
eqn = m*a == -m*g*sin(theta)

eqn(t) = $$a\hspace{0.17em}m=-g\hspace{0.17em}m\hspace{0.17em}\sin \left(\theta \left(t\right)\right)$$

For a pendulum with length $$r$$, the acceleration of the pendulum bob is equal to the angular acceleration times $$r$$.

$$a=r\frac{d^2\theta }{d{t}^2}$$.

Substitute for $$a$$ by using subs.

syms r
eqn = subs(eqn,a,r*diff(theta,2))

eqn(t) = 
$$m\hspace{0.17em}r\hspace{0.17em}\frac{{\partial }^2}{\partial t^2}\mathrm{ }\theta \left(t\right)=-g\hspace{0.17em}m\hspace{0.17em}\sin \left(\theta \left(t\right)\right)$$

Isolate the angular acceleration in eqn by using isolate.

eqn = isolate(eqn,diff(theta,2))

eqn = 
$$\frac{{\partial }^2}{\partial t^2}\mathrm{ }\theta \left(t\right)=-\frac{g\hspace{0.17em}\sin \left(\theta \left(t\right)\right)}{r}$$

Collect the constants $$g$$ and $$r$$ into a single parameter, which is also known as the natural frequency.

${\omega }_0=\sqrt{\frac{\mathit{g}}{\mathit{r}}}$.

syms omega_0
eqn = subs(eqn,g/r,omega_0^2)

eqn = 
$$\frac{{\partial }^2}{\partial t^2}\mathrm{ }\theta \left(t\right)=-{{\omega }_0}^2\hspace{0.17em}\sin \left(\theta \left(t\right)\right)$$

Step 2: Linearize the Equation of Motion

The equation of motion is nonlinear, so it is difficult to solve analytically. Assume the angles are small and linearize the equation by using the Taylor expansion of $$\sin \theta$$.

syms x
approx = taylor(sin(x),x,'Order',2);
approx = subs(approx,x,theta(t))

approx = $$\theta \left(t\right)$$

The equation of motion becomes a linear equation.

eqnLinear = subs(eqn,sin(theta(t)),approx)

eqnLinear = 
$$\frac{{\partial }^2}{\partial t^2}\mathrm{ }\theta \left(t\right)=-{{\omega }_0}^2\hspace{0.17em}\theta \left(t\right)$$

Step 3: Solve Equation of Motion Analytically

Solve the equation eqnLinear by using dsolve. Specify initial conditions as the second argument. Simplify the solution by assuming $${\omega }_0$$ is real using assume.

syms theta_0 theta_t0
theta_t = diff(theta);
cond = [theta(0) == theta_0, theta_t(0) == theta_t0];
assume(omega_0,'real')
thetaSol(t) = dsolve(eqnLinear,cond)

thetaSol(t) = 
$${\theta }_0\hspace{0.17em}\cos \left({\omega }_0\hspace{0.17em}t\right)+\frac{{\theta }_{\mathrm{t0}}\hspace{0.17em}\sin \left({\omega }_0\hspace{0.17em}t\right)}{{\omega }_0}$$

Step 4: Physical Significance of $${\omega }_0$$

The term $${\omega }_{0}t$$ is called the phase. The cosine and sine functions repeat every $$2\pi$$. The time needed to change $${\omega }_{0}t$$ by $$2\pi$$ is called the time period.

$$T=\frac{2\pi }{{\omega }_0}=2\pi \sqrt{\frac{r}{g}}$$.

The time period $$T$$ is proportional to the square root of the length of the pendulum and it does not depend on the mass. For linear equation of motion, the time period does not depend on the initial conditions.

Step 5: Plot Pendulum Motion

Plot the motion of the pendulum for small-angle approximation.

Define the physical parameters:

gValue = 9.81;
rValue = 1;
omega_0Value = sqrt(gValue/rValue);
T = 2*pi/omega_0Value;

Set initial conditions.

theta_0Value  = 0.1*pi; % Solution only valid for small angles.
theta_t0Value = 0;      % Initially at rest.

Substitute the physical parameters and initial conditions into the general solution.

vars   = [omega_0      theta_0      theta_t0];
values = [omega_0Value theta_0Value theta_t0Value];
thetaSolPlot = subs(thetaSol,vars,values);

Plot the harmonic pendulum motion.

fplot(thetaSolPlot(t*T)/pi, [0 5]);
grid on;
title('Harmonic Pendulum Motion');
xlabel('t/T');
ylabel('\theta/\pi');

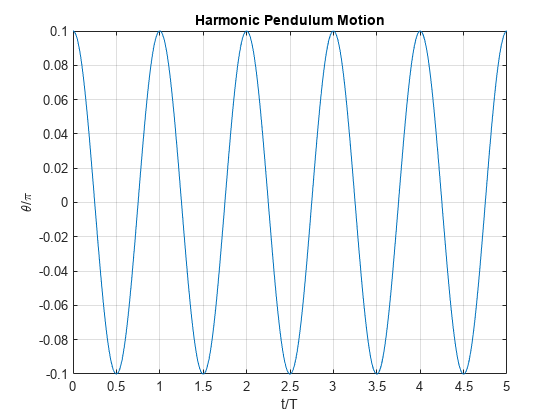
After finding the solution for $$\theta (t)$$, visualize the motion of the pendulum.

x_pos = sin(thetaSolPlot);
y_pos = -cos(thetaSolPlot);
fanimator(@fplot,x_pos,y_pos,'ko','MarkerFaceColor','k','AnimationRange',[0 5*T]);
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'),'AnimationRange',[0 5*T]);
fanimator(@(t) text(-0.3,0.3,"Timer: "+num2str(t,2)+" s"),'AnimationRange',[0 5*T]);

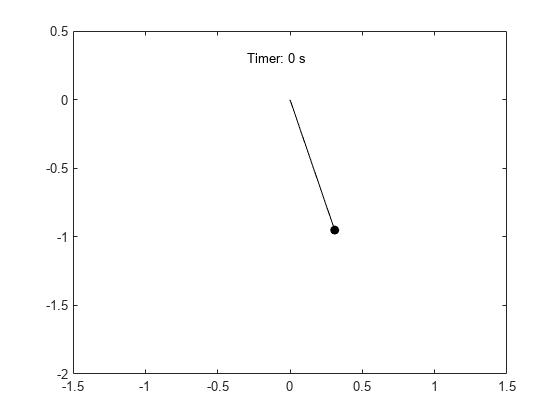
Enter the command playAnimation to play the animation of the pendulum motion.

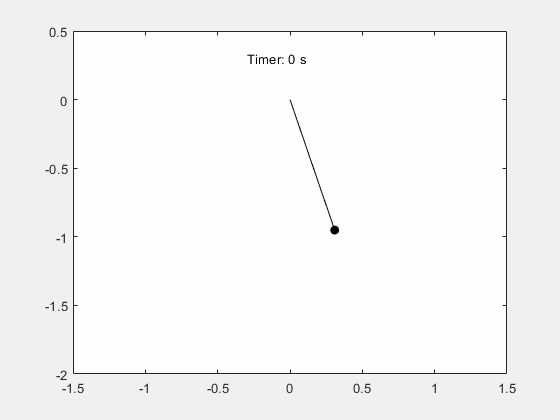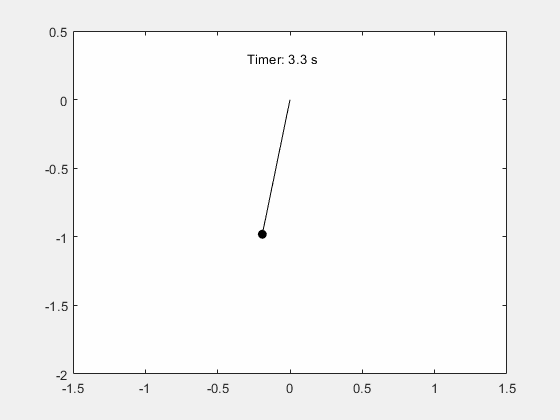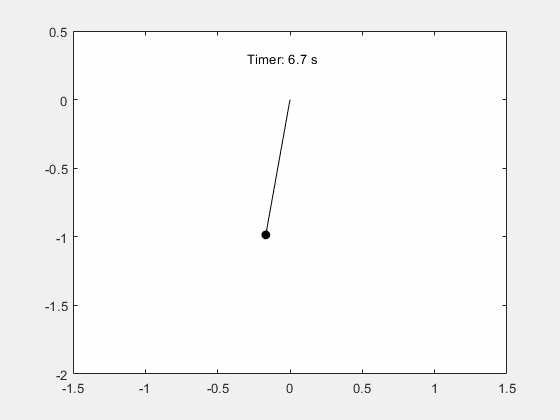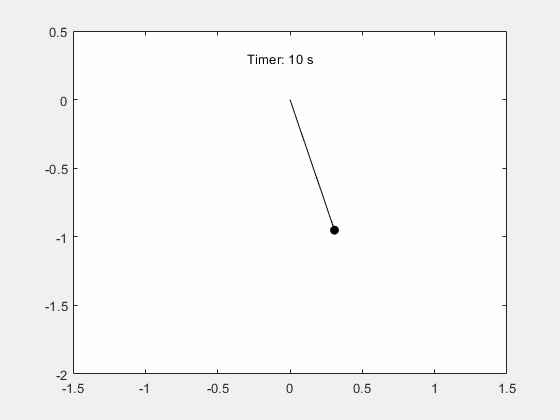
Step 6: Determine Nonlinear Pendulum Motion Using Constant Energy Paths

To understand the nonlinear motion of the pendulum, visualize the pendulum path by using the equation for total energy. The total energy is conserved.

Use the trigonometric identity $$1-\cos \theta =2{\sin }^2(\theta /2)$$ and the relation $${\omega }_0=\sqrt{g/r}$$ to rewrite the scaled energy.

Since energy is conserved, the motion of the pendulum can be described by constant energy paths in the phase space. The phase space is an abstract space with the coordinates $$\theta$$ and $$d\theta /dt$$. Visualize these paths using fcontour.

syms theta theta_t omega_0
E(theta, theta_t, omega_0) = (1/2)*(theta_t^2+(2*omega_0*sin(theta/2))^2);
Eplot(theta, theta_t) = subs(E,omega_0,omega_0Value);

figure;
fc = fcontour(Eplot(pi*theta, 2*omega_0Value*theta_t), 2*[-1 1 -1 1], ...
    'LineWidth', 2, 'LevelList', 0:5:50, 'MeshDensity', 1+2^8);
grid on;
title('Constant Energy Contours in Phase Space ( \theta vs. \theta_t )');
xlabel('\theta/\pi');
ylabel('\theta_t/2\omega_0');

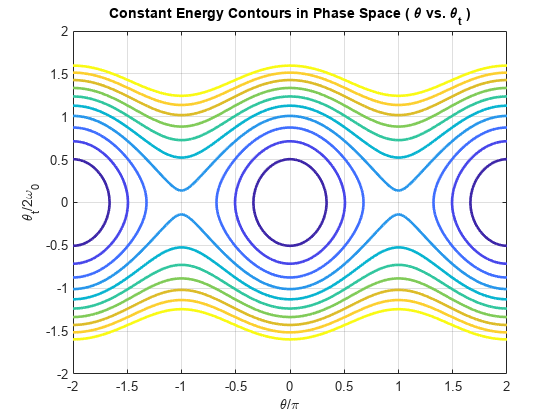
The constant energy contours are symmetric about the $$\theta$$ axis and $$d\theta /dt$$ axis, and are periodic along the $$\theta$$ axis. The figure shows two regions of distinct behavior.

The lower energies of the contour plot close upon themselves. The pendulum swings back and forth between two maximum angles and velocities. The kinetic energy of the pendulum is not enough to overcome gravitational energy and enable the pendulum to make a full loop.

The higher energies of the contour plot do not close upon themselves. The pendulum always moves in one angular direction. The kinetic energy of the pendulum is enough to overcome gravitational energy and enable the pendulum to make a full loop.

Step 7: Solve Nonlinear Equations of Motion

The nonlinear equations of motion are second-order differential equations. Numerically solve these equations by using the ode45 solver. Because ode45 accepts only first-order systems, reduce the system to a first-order system. Then, generate function handles that are the input to ode45.

Rewrite the second-order ODE as a system of first-order ODEs.

syms theta(t) theta_t(t) omega_0
eqs = [diff(theta)   == theta_t;
       diff(theta_t) == -omega_0^2*sin(theta)]

eqs(t) = 
$$\left(\begin{array}{c}\frac{\partial }{\partial t}\mathrm{ }\theta \left(t\right)={\theta }_t\left(t\right)\\ \frac{\partial }{\partial t}\mathrm{ }{\theta }_t\left(t\right)=-{{\omega }_0}^2\hspace{0.17em}\sin \left(\theta \left(t\right)\right)\end{array}\right)$$

eqs  = subs(eqs,omega_0,omega_0Value);
vars = [theta, theta_t];

Find the mass matrix M of the system and the right sides of the equations F.

[M,F] = massMatrixForm(eqs,vars)

M = 
$$\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$$

F = 
$$\left(\begin{array}{c}{\theta }_t\left(t\right)\\ -\frac{981\hspace{0.17em}\sin \left(\theta \left(t\right)\right)}{100}\end{array}\right)$$

M and F refer to this form.

To simplify further computations, rewrite the system in the form $$dx/dt=f(t,x(t))$$.

f = M\F

f = 
$$\left(\begin{array}{c}{\theta }_t\left(t\right)\\ -\frac{981\hspace{0.17em}\sin \left(\theta \left(t\right)\right)}{100}\end{array}\right)$$

Convert f to a MATLAB function handle by using odeFunction. The resulting function handle is the input to the MATLAB ODE solver ode45.

f = odeFunction(f, vars)

f = function_handle with value:
    @(t,in2)[in2(2,:);sin(in2(1,:)).*(-9.81e+2./1.0e+2)]

Step 8: Solve Equation of Motion for Closed Energy Contours

Solve the ODE for the closed energy contours by using ode45.

From the energy contour plot, closed contours satisfy the condition $${\theta }_0=0$$, $${\theta }_{t0}/2{\omega }_0\le 1$$. Store the initial conditions of $$\theta$$ and $$d\theta /dt$$ in the variable x0.

x0 = [0; 1.99*omega_0Value];

Specify a time interval from 0 s to 10 s for finding the solution. This interval allows the pendulum to go through two full periods.

tInit  = 0;
tFinal = 10;

Solve the ODE.

sols = ode45(f,[tInit tFinal],x0)

sols = struct with fields:
     solver: 'ode45'
    extdata: [1x1 struct]
          x: [0 3.2241e-05 1.9344e-04 9.9946e-04 0.0050 0.0252 0.1259 0.3449 0.6020 0.8591 1.1161 1.3597 1.5996 1.8995 2.2274 2.4651 2.7028 2.9567 3.2138 3.4709 3.7150 3.9511 4.2483 4.5759 4.8239 5.0719 5.3182 5.5764 5.8346 6.0803 ... ] (1x45 double)
          y: [2x45 double]
      stats: [1x1 struct]
      idata: [1x1 struct]

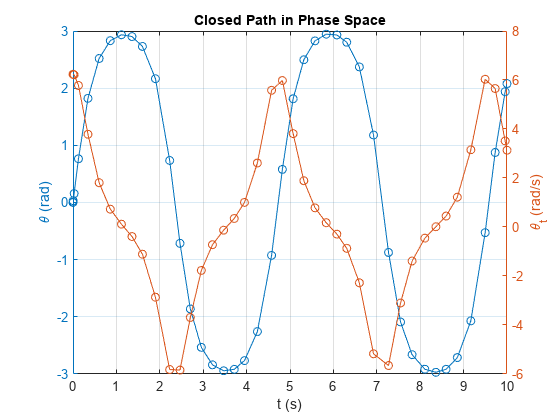
sols.y(1,:) represents the angular displacement $$\theta$$ and sols.y(2,:) represents the angular velocity $$d\theta /dt$$.

Plot the closed-path solution.

figure;

yyaxis left;
plot(sols.x, sols.y(1,:), '-o');
ylabel('\theta (rad)');

yyaxis right;
plot(sols.x, sols.y(2,:), '-o');
ylabel('\theta_t (rad/s)');

grid on;
title('Closed Path in Phase Space');
xlabel('t (s)');

Visualize the motion of the pendulum.

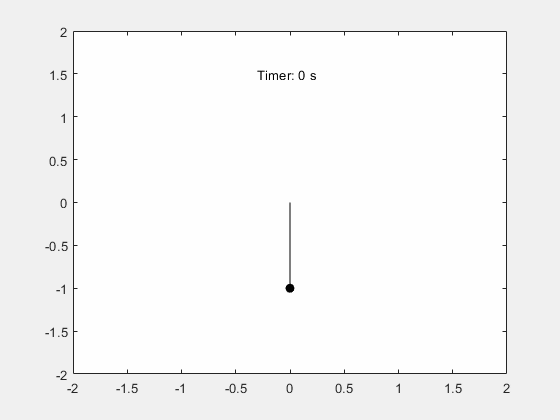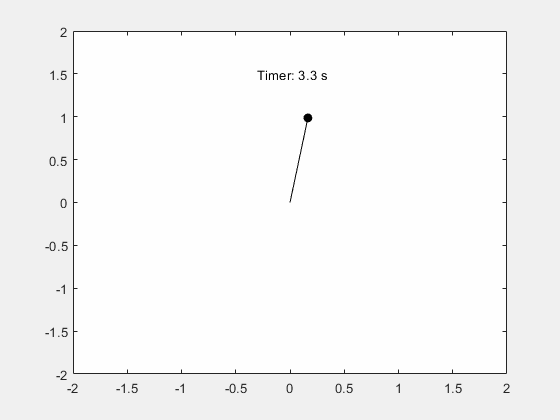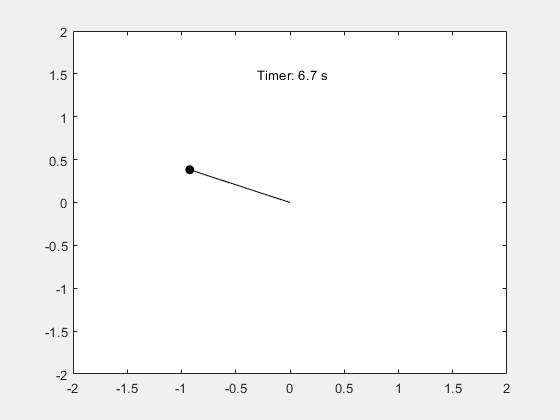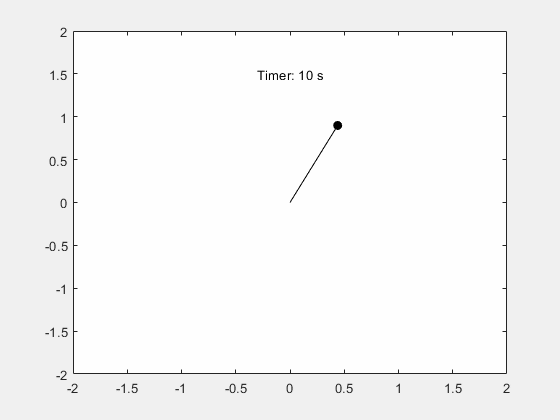
x_pos = @(t) sin(deval(sols,t,1));
y_pos = @(t) -cos(deval(sols,t,1));
figure;
fanimator(@(t) plot(x_pos(t),y_pos(t),'ko','MarkerFaceColor','k'));
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'));
fanimator(@(t) text(-0.3,1.5,"Timer: "+num2str(t,2)+" s"));

Enter the command playAnimation to play the animation of the pendulum motion.

Step 9: Solutions on Open Energy Contours

Solve the ODE for the open energy contours by using ode45. From the energy contour plot, open contours satisfy the condition $${\theta }_0=0$$, $${\theta }_{t0}/2{\omega }_0>1$$.

x0 = [0; 2.01*omega_0Value];
sols = ode45(f, [tInit, tFinal], x0);

Plot the solution for the open energy contour.

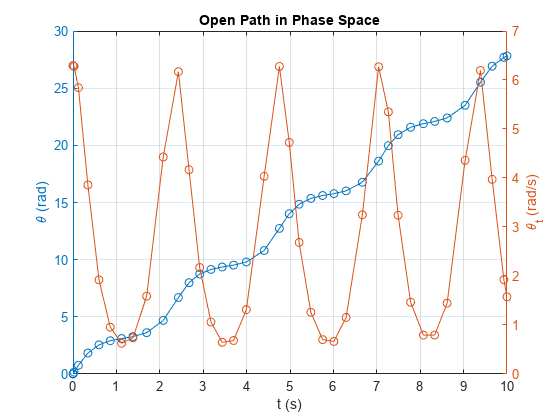
figure;

yyaxis left;
plot(sols.x, sols.y(1,:), '-o');
ylabel('\theta (rad)');

yyaxis right;
plot(sols.x, sols.y(2,:), '-o');
ylabel('\theta_t (rad/s)');

grid on;
title('Open Path in Phase Space');
xlabel('t (s)');

Visualize the motion of the pendulum.

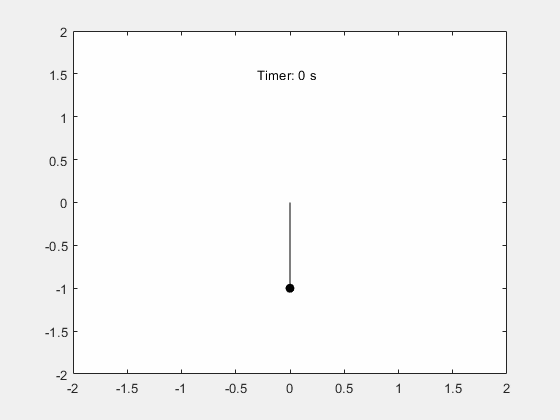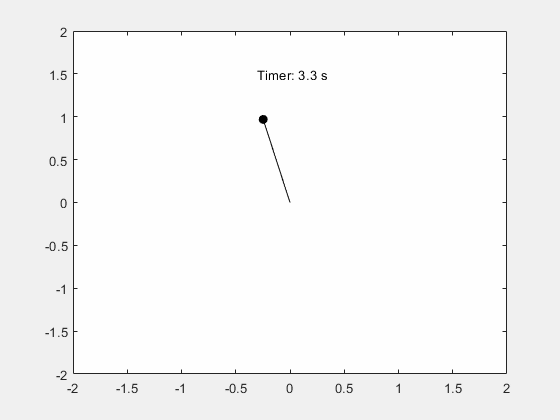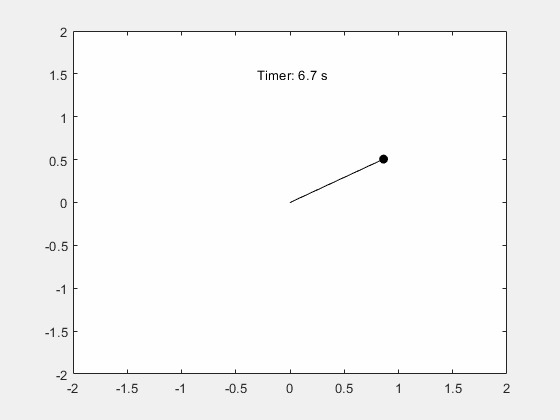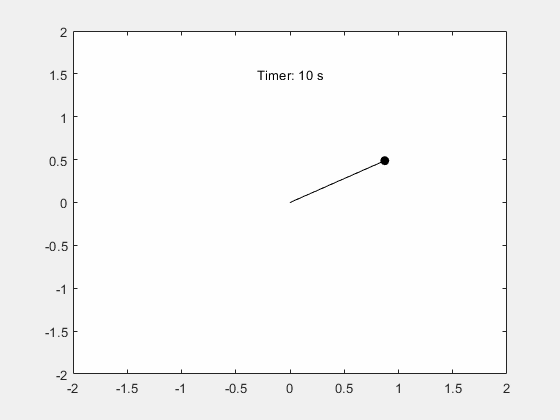
x_pos = @(t) sin(deval(sols,t,1));
y_pos = @(t) -cos(deval(sols,t,1));
figure;
fanimator(@(t) plot(x_pos(t),y_pos(t),'ko','MarkerFaceColor','k'));
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'));
fanimator(@(t) text(-0.3,1.5,"Timer: "+num2str(t,2)+" s"));

Enter the command playAnimation to play the animation of the pendulum motion.