C2000 PID Controller

Digital PID controller

Description

Replace the existing DMC blocks with MCB blocks for improved usability and future compatibility. It is recommended that you use blocks from Control Algorithm Design (Motor Control Blockset). While these blocks are not one-to-one replacements, they enable you to achieve the same functionality.

C28x DMC lib	C28x DMC lib equivalent in MCB
C2000 Clarke Transformation	Clarke Transform (Motor Control Blockset)
C2000 Inverse Park Transformation	Inverse Park Transform (Motor Control Blockset)
C2000 Park Transformation	Park Transform (Motor Control Blockset)
C2000 PID Controller	PI Controller (Motor Control Blockset)
C2000 Ramp Control	Position Generator (Motor Control Blockset)
C2000 Ramp Generator	Position Generator (Motor Control Blockset)
C2000 Space Vector Generator	PWM Reference Generator (Motor Control Blockset)
C2000 Speed Measurement	Speed Measurement (Motor Control Blockset)

This block implements a 32-bit digital PID controller with antiwindup correction. The inputs are a reference input (ref) and a feedback input (fdb) and the output (out) is the saturated PID output. The following diagram shows a PID controller with antiwindup.

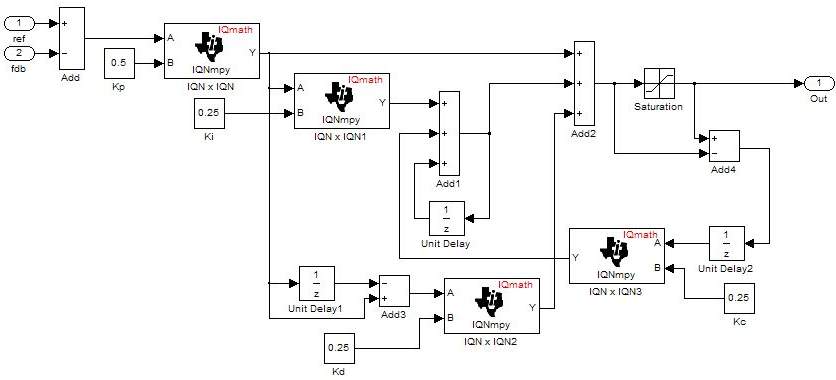
The differential equation describing the PID controller before saturation that is implemented in this block is

upresat(t) = up(t) + ui(t) + ud(t)

(1)

where u_presat is the PID output before saturation, u_p is the proportional term, u_i is the integral term with saturation correction, and u_d is the derivative term.

The proportional term is

up(t) = Kpe(t)

(2)

where K_p is the proportional gain of the PID controller and e(t) is the error between the reference and feedback inputs.

The integral term with saturation correction is

where K_c is the integral correction gain of the PID controller.

The derivative term is

where T_d is the derivative time of the PID controller. In discrete terms, the derivative gain is defined as K_d = T_d/T, and the integral gain is defined as K_i = T/T_i, where T is the sampling period and T_i is the integral time of the PID controller.

Using backward approximation, the preceding differential equations can be transformed into the following discrete equations.

Note

• To generate optimized code from this block, enable the TI C28x or TI C28x (ISO) Code Replacement Library.

  The implementation of this block does not call the corresponding Texas Instruments^® library function during code generation. The TI function uses a global Q setting and the MathWorks^® code used by this block dynamically adjusts the Q format based on the block input. See Using the IQmath Library for more information.

This block implements a 32-bit digital PID controller with antiwindup correction. The inputs are a reference input (ref) and a feedback input (fdb) and the output (out) is the saturated PID output. The following diagram shows a PID controller with antiwindup.

The differential equation describing the PID controller before saturation that is implemented in this block is

upresat(t) = up(t) + ui(t) + ud(t)

(3)

where u_presat is the PID output before saturation, u_p is the proportional term, u_i is the integral term with saturation correction, and u_d is the derivative term.

The proportional term is

up(t) = Kpe(t)

(4)

where K_p is the proportional gain of the PID controller and e(t) is the error between the reference and feedback inputs

where K_c is the integral correction gain of the PID controller.

The derivative term is

where T_d is the derivative time of the PID controller. In discrete terms, the derivative gain is defined as K_d = T_d/T, and the integral gain is defined as K_i = T/T_i, where T is the sampling period and T_i is the integral time of the PID controller.

Using backward approximation, the preceding differential equations can be transformed into the following discrete equations.

Note

• To generate optimized code from this block, enable the TI C28x or TI C28x (ISO) Code Replacement Library.

  The implementation of this block does not call the corresponding Texas Instruments library function during code generation. The TI function uses a global Q setting and the MathWorks code used by this block dynamically adjusts the Q format based on the block input. See Using the IQmath Library for more information.

• 

Parameters

Proportional gain

Amount of proportional gain (K_p) to apply to the PID

Integral gain

Amount of gain (K_i) to apply to the integration equation

Integral correction gain

Amount of correction gain (K_c) to apply to the integration equation

Derivative gain

Amount of gain (K_d) to apply to the derivative equation.

Minimum output

Minimum allowable value of the PID output

Maximum output

Maximum allowable value of the PID output

References

For detailed information on the DMC library, see C/F 28xx Digital Motor Control Library, Literature Number SPRC080, available at the Texas Instruments Web site.