C2000 Ramp Generator
Generate ramp output
Description
Replace the existing DMC blocks with MCB blocks for improved usability and future compatibility. It is recommended that you use blocks from Control Algorithm Design (Motor Control Blockset). While these blocks are not one-to-one replacements, they enable you to achieve the same functionality.
| C28x DMC lib | C28x DMC lib equivalent in MCB |
|---|---|
| C2000 Clarke Transformation | Clarke Transform (Motor Control Blockset) |
| C2000 Inverse Park Transformation | Inverse Park Transform (Motor Control Blockset) |
| C2000 Park Transformation | Park Transform (Motor Control Blockset) |
| C2000 PID Controller | PI Controller (Motor Control Blockset) |
| C2000 Ramp Control | Position Generator (Motor Control Blockset) |
| C2000 Ramp Generator | Position Generator (Motor Control Blockset) |
| C2000 Space Vector Generator | PWM Reference Generator (Motor Control Blockset) |
| C2000 Speed Measurement | Speed Measurement (Motor Control Blockset) |
This block generates ramp output (out) from the slope of the
ramp signal (gain), DC offset in the ramp signal
(offset), and frequency of the ramp signal (freq)
inputs. All of the inputs and output are 32-bit fixed-point
numbers with Q values between 1 and 29.
Algorithm
The block's output (out) at the sampling instant
k is governed by the following algorithm:
out(k) = angle(k)
* gain(k) +
offset(k) | (1) |
For out(k) > 1,
out(k) =
out(k) - 1. For
out(k) < -1,
out(k) =
out(k) + 1.
Angle(k) is defined as follows:
angle(k) = angle(k-1) +
freq(k) * Maximum step
angle | (2) |
| for angle(k) > 1, angle(k) = angle(k) - 1 | (3) |
| for angle(k) < -1, angle(k) = angle(k) + 1 | (4) |
The frequency of the ramp output is controlled by a precision frequency generation algorithm that relies on the modulo nature of the finite length variables. The frequency of the output ramp signal is equal to
| f = (Maximum step angle * sampling rate) / 2m | (5) |
where m represents the fractional length of the data type of the inputs.
All math operations are carried out in fixed-point arithmetic, where the fixed-point fractional length is determined by the block's inputs.
Note
To generate optimized code from this block, enable the TI
C28x or TI C28x (ISO) Code Replacement
Library.
Parameters
- Maximum step angle
The maximum step size, which determines the rate of change of the output (i.e., the minimum period of the ramp signal).
When you enter double-precision floating-point values for parameters in the IQ Math blocks, the software converts them to single-precision values that are compatible with the behavior on c28x processor.
Examples
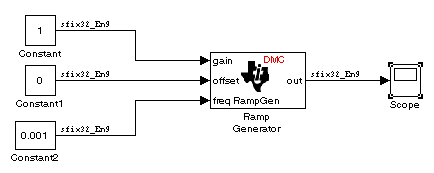
The following model demonstrates the Ramp Generator block. The Constant and Scope blocks are available in Simulink® Commonly Used Blocks.
In your model, select Simulation > Model Configuration
Parameters. On the
Solver pane, set Type to
Fixed-step and Solver to
Discrete (no continuous states).
Set the parameter values for the blocks as shown in the following table.
Block | Connects to | Parameter | Value |
|---|---|---|---|
Ramp Generator - |
|
| |
Ramp Generator - |
|
| |
Ramp Generator - |
|
| |
Scope and Floating Scope (Simulink block) |
|
|
When you run the model, the Scope block generates the following output (drag a zoom box around a portion of the output to change the display).
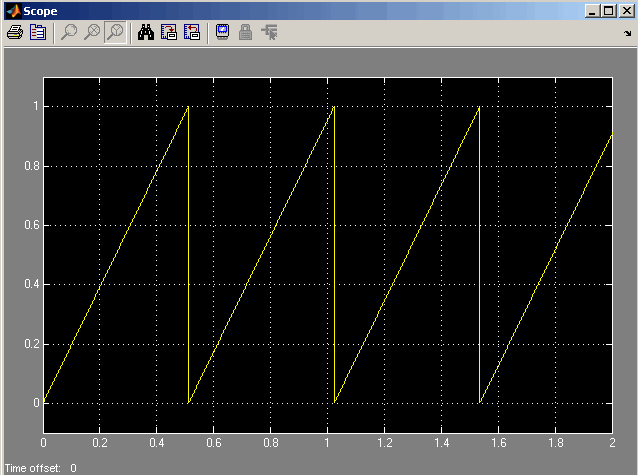
With fixed point calculations in IQMath, for a given frequency input on the block, f_input, the equation is:
| f = (Maximum step angle * f_input * sampling rate) / 2m | (6) |
For example, if f_input = 0.001, the real value, 1, counts as fixed point with a fractional length of 9:
| f = (1 * 1 * (1/0.001) ) / 29 = 1.9531 Hz | (7) |
Where 0.001 is the block sample time.
If we use normal math, and f_input is a non-fixed point real value, then:
| f = (Maximum step angle * f_input * sampling rate) / 1 | (8) |
For example, if we are using floating point calculation:
| f = (1 * 0.001 * (1/0.001) ) / 1 = 1 Hz | (9) |
When using fixed point with fractional length 9, the expected period becomes:
| T = 1/f = 1/1.9531 Hz = 0.5120 s | (10) |
This result is what the above Scope output shows.
Note
If you use different fractional lengths for the fixed point calculations, the output frequency varies depending on the precision.