- /
-
Ned check this out (5.3)
on 24 Oct 2021
- 3
- 65
- 1
- 0
- 274
% This is a traveling salesman problem.
% Use the cities defined by x
rng(0)
n=30;
x=rand(n,1)+1i*rand(n,1);
% Generate distance matrix d
d=abs(x-x.');
% Ned This should be your function but a lil bit shorter
L=@(r)sum(d(sub2ind([n n],r,r([end 1:end-1]))));
% distance in a subset of the combination-list index:
% I give a permutation matrix "i" based on the subset of indexes->
% for every row I get the distance path from I(row,1) to I(row,end)
S=@(i) sum(d((i(:,1:end-1)-1)*n+i(:,2:end)),2);
% better Pre-set (P) of the list order i found in few attempts, without this
% reroll I got at the first attempt something like "score=8.5"
% for y=1:5
% P=randperm(30);
% end --> rerolling 5 times the preset gave me a "score=7.2"
% But then I thougth: "Why not sort the indexes based on the points real component?"
% Thats my new preset:
[~,P]=sort(real(x));
s=[];
% Solution search starts now: splitting the preset-list in 3 subsets and optimize them
% locally
for j=1:3
% Getting for the j-th subset the permutation that minimizes the path (without closing the loop)
% 1) compute permutation matrix "U" of the preset(1:10), then preset(11:20) and then preset(21:30)
% 2) calculate all the local path distances and keeping only the shortest
% one. To be sure: I don't keep the cost, but the index of the permutation associated to it
% 3) Building the main solution with the local solution "U(idx_solution,:)"
U=perms(P((j-1)*10+(1:10)));
[~,i]=min(S(U));
s=[s U(i,:)];
end
% Thats the index solution to me. But now let's calculate the score based
% on Ned's function cost (where the path is computed linking the 1st and the last point)
s
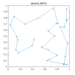
plot(x(s),'o-')
% computing and displaying Ned's distance function.
title("dist="+L(s))
axis square