Architettura della rete neurale superficiale multilivello

Questo argomento presenta parte di un tipico workflow di una rete superficiale multilivello. Per ulteriori informazioni e altri passaggi, vedere Reti neurali superficiali multilivello e addestramento sulla retropropagazione.

Modello di neurone (logsig, tansig, purelin)

Di seguito, viene mostrato un neurone elementare con input R. Ciascun input è ponderato con un'appropriata w. La somma degli input ponderati e del bias costituisce gli input della funzione di trasferimento f. I neuroni possono utilizzare qualsiasi funzione di trasferimento differenziabile f per generare l'output.

Schematic diagram of a general neuron. The neuron multiplies a input vector p by a weights vector w, sums the result, and applies a bias b. A transfer function f is then applied, generating output a.

Le reti multilivello utilizzano spesso la funzione di trasferimento a sigmoide logaritmica logsig.

A plot of the log-sigmoid transfer function. For large positive inputs, the output tends to +1. For large negative inputs, the output tends to 0. An input of 0 gives an output of 0.5.

La funzione logsig genera output compresi tra 0 e 1 al progredire dell'input netto del neurone dall'infinito negativo all'infinito positivo.

In alternativa, le reti multilivello possono utilizzare la funzione di trasferimento tan-sigmoidale tansig.

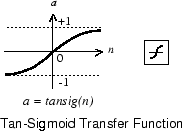
A plot of the tan-sigmoid transfer function. For large positive inputs, the output tends to +1. For large negative inputs, the output tends to -1. An input of 0 gives an output of 0.

I neuroni di output sigmoidali sono spesso utilizzati per problemi di pattern recognition mentre i neuroni di output lineari sono utilizzati per problemi di adattamento delle funzioni. Di seguito, viene mostrata la funzione di trasferimento lineare purelin.

A plot of the linear transfer function. The output scales linearly with the input.

Le tre funzioni di trasferimento qui descritte sono le funzioni di trasferimento più comunemente utilizzate per le reti multilivello, ma se lo si desidera è possibile creare e utilizzare altre funzioni di trasferimento differenziabili.

Rete neurale feed-forward

Una rete a singolo livello di neuroni S logsig con R input viene mostrata qui di seguito nel dettaglio sulla sinistra, con un diagramma dei livelli sulla destra.

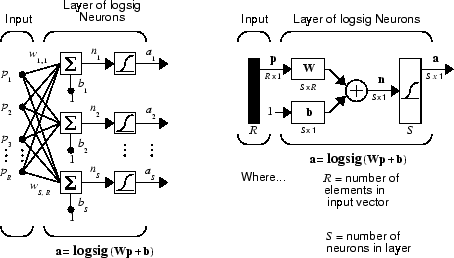
Schematic diagram showing a layer containing S logsig neurons.

Le reti feed-forward presentano spesso uno o più livelli nascosti di neuroni sigmoidali seguiti da un livello di output di neuroni lineari. Livelli multipli di neuroni con funzioni di trasferimento non lineari consento alla rete di apprendere le relazioni non lineari tra i vettori di input e i vettori di output. Il livello di output lineare è utilizzato principalmente per i problemi di adattamento delle funzioni (o di regressione non lineare).

Se invece si desidera vincolare gli output di una rete (ad esempio tra 0 e 1), il livello di output dovrebbe utilizzare una funzione di trasferimento sigmoidale (come logsig). Questo è il caso in cui la rete è utilizzata per problemi di pattern recognition (nei quali la decisione viene presa dalla rete).

Per le reti multilivello, il numero del livello determina l'apice della matrice ponderale. La notazione appropriata è utilizzata nella rete a due livelli tansig/purelin mostrata di seguito.

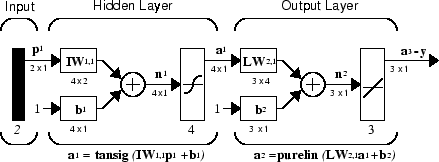
A schematic diagram of a network containing two layers. A hidden layer receives an input vector p. The weights of the hidden layer are denoted with a superscript 1. An output layer receives the output of the hidden layer. The weights of the output layer are denoted with a superscript 1.

Questa rete può essere utilizzata come approssimatore generale di funzioni. Può approssimare arbitrariamente qualsiasi funzione con un numero finito di discontinuità in modo corretto, dato un numero sufficiente di neuroni nel livello nascosto.

Adesso che l'architettura della rete multilivello è stata definita, nelle sezioni seguenti viene descritto il processo di progettazione.