graphplot
Plot Markov chain directed graph
Description
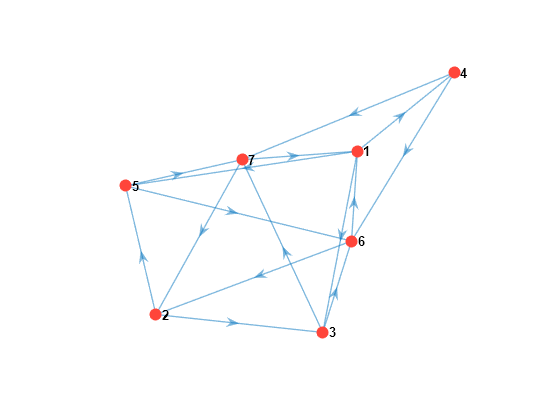
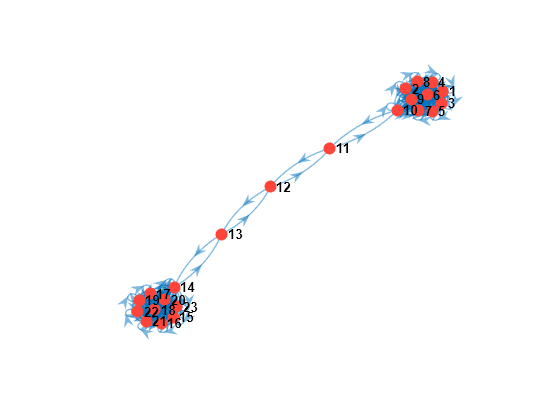
graphplot( creates a plot of the directed graph (digraph) of the discrete-time Markov chain mc)mc. Nodes correspond to the states of mc. Directed edges correspond to nonzero transition probabilities in the transition matrix mc.P.
graphplot(
uses additional
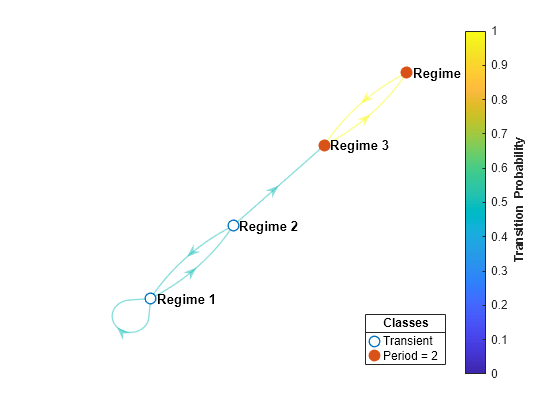
options specified by one or more name-value arguments. Options include highlighting transition probabilities, communicating classes, and specifying class properties of recurrence/transience and period. Also, you can plot the condensed digraph instead, with communicating classes as supernodes.mc,Name,Value)
graphplot(
plots on the axes specified by ax,___)ax instead of the current axes (gca) using any of the input argument combinations in the previous syntaxes. The option ax can precede any of the input argument combinations in the previous syntaxes.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
To produce the directed graph as a MATLAB®
digraphobject and use additional functions of that object, enter:G = digraph(mc.P)
For readability, the
'LabelNodes'name-value pair argument allows you to turn off lengthy node labels and replace them with node numbers. To remove node labels completely, seth.NodeLabel = {};.To compute node information on communicating classes and their properties, use
classify.To extract a communicating class in the graph, use
subchain.The condensed graph is useful for:
Identifying transient classes (supernodes with positive outdegree)
Identifying recurrent classes (supernodes with zero outdegree)
Visualizing the overall structure of unichains (chains with a single recurrent class and any transient classes that transition into it)
References
[1] Gallager, R.G. Stochastic Processes: Theory for Applications. Cambridge, UK: Cambridge University Press, 2013.
[2] Horn, R., and C. R. Johnson. Matrix Analysis. Cambridge, UK: Cambridge University Press, 1985.
[3] Jarvis, J. P., and D. R. Shier. "Graph-Theoretic Analysis of Finite Markov Chains." In Applied Mathematical Modeling: A Multidisciplinary Approach. Boca Raton: CRC Press, 2000.
Version History
Introduced in R2017b