updateMetrics
Update performance metrics in naive Bayes incremental learning classification model given new data
Since R2021a
Description
Given streaming data, updateMetrics measures the performance of a configured naive Bayes classification model for incremental learning (incrementalClassificationNaiveBayes object). updateMetrics stores the performance metrics in the output model.
updateMetrics allows for flexible incremental learning. After you call the function to update model performance metrics on an incoming chunk of data, you can perform other actions before you train the model to the data. For example, you can decide whether you need to train the model based on its performance on a chunk of data. Alternatively, you can both update model performance metrics and train the model on the data as it arrives, in one call, by using the updateMetricsAndFit function.
To measure the model performance on a specified batch of data, call loss instead.
Mdl = updateMetrics(Mdl,X,Y)Mdl, which is the input naive Bayes classification model for incremental learning Mdl modified to contain the model performance metrics on the incoming predictor and response data, X and Y respectively.
When the input model is warm (Mdl.IsWarm is true), updateMetrics overwrites previously computed metrics, stored in the Metrics property, with the new values. Otherwise, updateMetrics stores NaN values in Metrics instead.
Examples
Train a naive Bayes classification model by using fitcnb, convert it to an incremental learner, and then track its performance to streaming data.
Load and Preprocess Data
Load the human activity data set. Randomly shuffle the data.
load humanactivity rng(1) % For reproducibility n = numel(actid); idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Train Naive Bayes Classification Model
Fit a naive Bayes classification model to a random sample of half the data.
idxtt = randsample([true false],n,true); TTMdl = fitcnb(X(idxtt,:),Y(idxtt))
TTMdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
NumObservations: 12053
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
TTMdl is a ClassificationNaiveBayes model object representing a traditionally trained model.
Convert Trained Model
Convert the traditionally trained classification model to a naive Bayes classification model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationNaiveBayes
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
The incremental model is warm. Therefore, updateMetrics can track model performance metrics given data.
Track Performance Metrics
Track the model performance on the rest of the data by using the updateMetrics function. Simulate a data stream by processing 50 observations at a time. At each iteration:
Call
updateMetricsto update the cumulative and window minimal cost of the model given the incoming chunk of observations. Overwrite the previous incremental model to update the losses in theMetricsproperty. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model.Store the minimal cost and mean of the first predictor in the first class .
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 50; nchunk = floor(nil/numObsPerChunk); mc = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); mu11 = [IncrementalMdl.DistributionParameters{1,1}(1); zeros(nchunk+1,1)]; Xil = X(idxil,:); Yil = Y(idxil); % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx)); mc{j,:} = IncrementalMdl.Metrics{"MinimalCost",:}; mu11(j + 1) = IncrementalMdl.DistributionParameters{1,1}(1); end
IncrementalMdl is an incrementalClassificationNaiveBayes model object that has tracked the model performance to observations in the data stream.
Plot a trace plot of the performance metrics and .
t = tiledlayout(2,1); nexttile h = plot(mc.Variables); xlim([0 nchunk]) ylabel('Minimal Cost') legend(h,mc.Properties.VariableNames) nexttile plot(mu11) ylabel('\mu_{11}') xlim([0 nchunk]) xlabel(t,'Iteration')
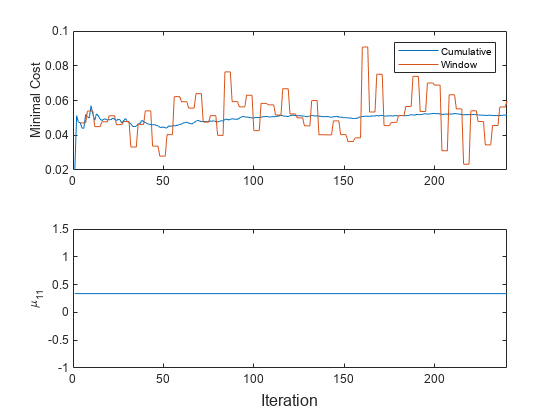
The cumulative loss is stable, whereas the window loss jumps throughout the training.
does not change because updateMetrics does not fit the model to the data.
Create a naive Bayes classification model for incremental learning by calling incrementalClassificationNaiveBayes and specifying a maximum of 5 expected classes in the data. Specify tracking misclassification error rate in addition to minimal cost.
Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',5,'Metrics',"classiferror");
Mdl is an incrementalClassificationNaiveBayes model. All its properties are read-only.
Determine whether the model is warm by querying the model property.
isWarm = Mdl.IsWarm
isWarm = logical
0
Mdl.IsWarm is 0; therefore, Mdl is not warm.
Determine the number of observations incremental fitting functions, such as fit, must process before measuring the performance of the model by displaying the size of the metrics warm-up period.
numObsBeforeMetrics = Mdl.MetricsWarmupPeriod
numObsBeforeMetrics = 1000
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Suppose that the data from a stationary subject (Y <= 2) has double the quality of the data from a moving subject. Create a weight variable that assigns a weight of 2 to observations from a stationary subject and 1 to a moving subject.
W = ones(n,1) + (Y <= 2);
Implement incremental learning by performing the following actions at each iteration:
Simulate a data stream by processing a chunk of 50 observations.
Measure model performance metrics on the incoming chunk using
updateMetrics. Specify the corresponding observation weights and overwrite the input model.Fit the model to the incoming chunk. Specify the corresponding observation weights and overwrite the input model.
Store and the misclassification error rate to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); ce = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); mu11 = zeros(nchunk,1); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx),'Weights',W(idx)); ce{j,:} = Mdl.Metrics{"ClassificationError",:}; Mdl = fit(Mdl,X(idx,:),Y(idx),'Weights',W(idx)); mu11(j) = Mdl.DistributionParameters{1,1}(1); end
Now, Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream.
To see how the parameters evolve during incremental learning, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(mu11) ylabel('\mu_{11}') xlabel('Iteration') axis tight nexttile plot(ce.Variables) ylabel('ClassificationError') xline(numObsBeforeMetrics/numObsPerChunk,'r-.') xlim([0 nchunk]) legend(ce.Properties.VariableNames) xlabel(t,'Iteration')
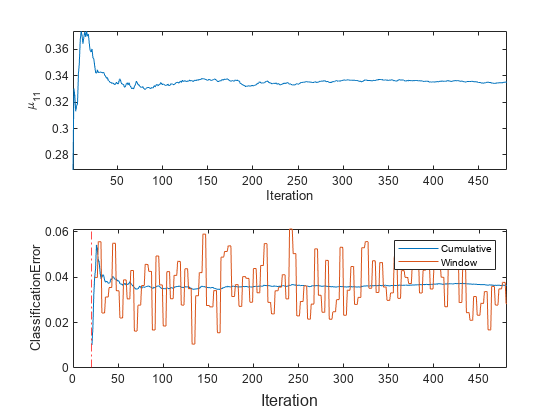
mdlIsWarm = numObsBeforeMetrics/numObsPerChunk
mdlIsWarm = 20
The plot suggests that fit always fits the model to the data, and updateMetrics does not track the classification error until after the metrics warm-up period (20 chunks).
Incrementally train a naive Bayes classification model only when its performance degrades.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Configure a naive Bayes classification model for incremental learning so that the maximum number of expected classes is 5, the tracked performance metric includes the misclassification error rate, and the metrics window size is 1000. Fit the configured model to the first 1000 observations.
Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',5,'MetricsWindowSize',1000, ... 'Metrics','classiferror'); initobs = 1000; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
Mdl is an incrementalClassificationNaiveBayes model object.
Perform incremental learning, with conditional fitting, by following this procedure for each iteration:
Simulate a data stream by processing a chunk of 100 observations at a time.
Update the model performance on the incoming chunk of data.
Fit the model to the chunk of data only when the misclassification error rate is greater than 0.05.
When tracking performance and fitting, overwrite the previous incremental model.
Store the misclassification error rate and the mean of the first predictor in the second class to see how they evolve during training.
Track when
fittrains the model.
% Preallocation numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); mu21 = zeros(nchunk,1); ce = array2table(nan(nchunk,2),'VariableNames',["Cumulative" "Window"]); trained = false(nchunk,1); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); ce{j,:} = Mdl.Metrics{"ClassificationError",:}; if ce{j,2} > 0.05 Mdl = fit(Mdl,X(idx,:),Y(idx)); trained(j) = true; end mu21(j) = Mdl.DistributionParameters{2,1}(1); end
Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream.
To see how the model performance and evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(mu21) hold on plot(find(trained),mu21(trained),'r.') xlim([0 nchunk]) ylabel('\mu_{21}') legend('\mu_{21}','Training occurs','Location','best') hold off nexttile plot(ce.Variables) xlim([0 nchunk]) ylabel('Misclassification Error Rate') legend(ce.Properties.VariableNames,'Location','best') xlabel(t,'Iteration')
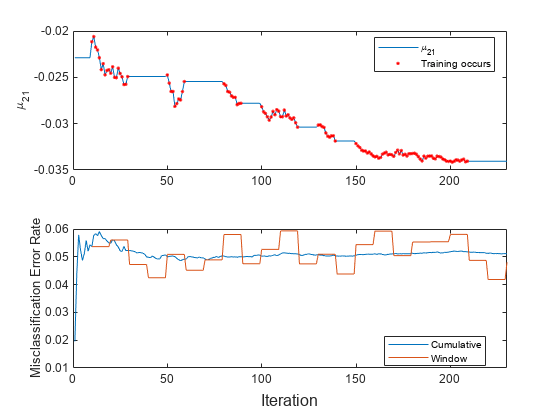
The trace plot of shows periods of constant values, during which the loss within the previous observation window is at most 0.05.
Input Arguments
Naive Bayes classification model for incremental learning to measure the performance
of, specified as an incrementalClassificationNaiveBayes model object. You can create
Mdl directly or by converting a supported, traditionally trained
machine learning model using the incrementalLearner function. For more details, see the corresponding
reference page.
If Mdl.IsWarm is false,
updateMetrics does not track the performance of the model. Before
updateMetrics can track performance metrics, you must perform all
the following actions:
Fit the input model
Mdlto all expected classes (see theMaxNumClassesandClassNamesarguments ofincrementalClassificationNaiveBayes).Fit the input model
MdltoMdl.MetricsWarmupPeriodobservations by passingMdland the data tofit. For more details, see Performance Metrics.
Chunk of predictor data to measure the model performance, specified as an
n-by-Mdl.NumPredictors floating-point
matrix.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row) in j)X.
Note
If Mdl.NumPredictors = 0, updateMetrics
infers the number of predictors from X, and sets the corresponding
property of the output model. Otherwise, if the number of predictor variables in the
streaming data changes from Mdl.NumPredictors,
updateMetrics issues an error.
Data Types: single | double
Chunk of labels with which to measure the model performance, specified as a categorical, character, or string array; logical or floating-point vector; or cell array of character vectors.
The length of the observation labels Y and the number of observations in
X must be equal; Y(
is the label of observation j (row) in j)X.
updateMetrics issues an error when one or both of these conditions are met:
Ycontains a new label and the maximum number of classes has already been reached (see theMaxNumClassesandClassNamesarguments ofincrementalClassificationNaiveBayes).The
ClassNamesproperty of the input modelMdlis nonempty, and the data types ofYandMdl.ClassNamesare different.
Data Types: char | string | cell | categorical | logical | single | double
Chunk of observation weights, specified as a floating-point vector of positive values.
updateMetrics weighs the observations in X
with the corresponding values in Weights. The size of
Weights must equal n, the number of
observations in X.
By default, Weights is ones(.n,1)
For more details, including normalization schemes, see Observation Weights.
Data Types: double | single
Note
If an observation (predictor or label) or weight contains at
least one missing (NaN) value, updateMetrics ignores the
observation. Consequently, updateMetrics uses fewer than n
observations to compute the model performance, where n is the number of
observations in X.
Output Arguments
Updated naive Bayes classification model for incremental learning, returned as an incremental learning model object of the same data type as the input model Mdl, an incrementalClassificationNaiveBayes object.
If the model is not warm, updateMetrics does
not compute performance metrics. As a result, the Metrics property of
Mdl remains completely composed of NaN values. If the
model is warm, updateMetrics computes the cumulative and window performance
metrics on the new data X and Y, and overwrites the
corresponding elements of Mdl.Metrics. All other properties of the input
model Mdl carry over to the output model Mdl. For more details, see
Performance Metrics.
Tips
Unlike traditional training, incremental learning might not have a separate test (holdout) set. Therefore, to treat each incoming chunk of data as a test set, pass the incremental model and each incoming chunk to
updateMetricsbefore training the model on the same data usingfit.
Algorithms
updateMetricstracks only model performance metrics, specified by the row labels of the table inMdl.Metrics, from new data only when the incremental model is warm (IsWarmproperty istrue).If you create an incremental model by using
incrementalLearnerandMetricsWarmupPeriodis 0 (default forincrementalLearner), the model is warm at creation.Otherwise, an incremental model becomes warm after the
fitfunction performs both of these actions:Fit the incremental model to
Mdl.MetricsWarmupPeriodobservations, which is the metrics warm-up period.Fit the incremental model to all expected classes (see the
MaxNumClassesandClassNamesarguments ofincrementalClassificationNaiveBayes).
Mdl.Metricsstores two forms of each performance metric as variables (columns) of a table,CumulativeandWindow, with individual metrics in rows. When the incremental model is warm,updateMetricsupdates the metrics at the following frequencies:Cumulative— The function computes cumulative metrics since the start of model performance tracking. The function updates metrics every time you call it and bases the calculation on the entire supplied data set.Window— The function computes metrics based on all observations within a window determined by theMdl.MetricsWindowSizeproperty.Mdl.MetricsWindowSizealso determines the frequency at which the software updatesWindowmetrics. For example, ifMdl.MetricsWindowSizeis 20, the function computes metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store a buffer of length
Mdl.MetricsWindowSizefor each specified metric, and store a buffer of observation weights.Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.
When the buffer is full, overwrite
Mdl.Metrics.Windowwith the weighted average performance in the metrics window. If the buffer is overfills when the function processes a batch of observations, the latest incomingMdl.MetricsWindowSizeobservations enter the buffer, and the earliest observations are removed from the buffer. For example, supposeMdl.MetricsWindowSizeis 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the function uses the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a
NaNscore when computing theCumulativeandWindowperformance metric values.
For each conditional predictor distribution, updateMetrics computes the weighted average and standard deviation.
If the prior class probability distribution is known (in other words, the prior distribution is not empirical), updateMetrics normalizes observation weights to sum to the prior class probabilities in the respective classes. This action implies that the default observation weights are the respective prior class probabilities.
If the prior class probability distribution is empirical, the software normalizes the specified observation weights to sum to 1 each time you call updateMetrics.
Version History
Introduced in R2021a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)