permutationImportance
Syntax
Description
Importance = permutationImportance(Mdl)Mdl by permuting
the values in the predictor and comparing the model resubstitution loss with the original
predictor to the loss with the permuted predictor. A large increase in the model loss with
the permuted predictor indicates that the predictor is important. By default, the function
repeats the process over 10 permutations, and then averages the values. For more
information, see Permutation Predictor Importance.
Mdl must be a full classification or regression model that contains
the training data. That is, Mdl.X and Mdl.Y must be
nonempty. The returned Importance table contains the importance mean
and standard deviation for each predictor computed over 10 permutations.
Importance = permutationImportance(Mdl,Tbl,ResponseVarName)Tbl and the response values in the
ResponseVarName table variable.
Importance = permutationImportance(Mdl,Tbl,Y)Tbl and the response values in variable
Y.
Importance = permutationImportance(Mdl,X,Y)X and the response values in variable Y.
Importance = permutationImportance(___,Name=Value)NumPermutations name-value argument to change the number of
permutations used to compute the mean and standard deviation of the predictor importance
values for each predictor.
[
also returns the importance values computed for each predictor and permutation.Importance,ImportancePerPermutation] = permutationImportance(___)
[
also returns the mean and standard deviation of the importance values for each predictor and
class in Importance,ImportancePerPermutation,ImportancePerClass] = permutationImportance(___)Mdl.ClassNames. You can use this syntax when
Mdl is a classification model and the LossFun
value is a built-in loss function. For more information, see Permutation Predictor Importance per Class.
Examples
Compute the mean permutation predictor importance for the predictors in a regression support vector machine (SVM) model.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG.
load carbig cars = table(Acceleration,Cylinders,Displacement, ... Horsepower,Model_Year,Weight,Origin,MPG);
Categorize the cars based on whether they were made in the USA.
cars.Origin = categorical(cellstr(cars.Origin)); cars.Origin = mergecats(cars.Origin,["France","Japan",... "Germany","Sweden","Italy","England"],"NotUSA");
Partition the data into two sets. Use approximately half of the observations for model training, and half of the observations for computing predictor importance.
rng("default") % For reproducibility c = cvpartition(size(cars,1),"Holdout",0.5); carsTrain = cars(training(c),:); carsImportance = cars(test(c),:);
Train a regression SVM model using the carsTrain training data. Specify to standardize the numeric predictors. By default, fitrsvm uses a linear kernel function to fit the model.
Mdl = fitrsvm(carsTrain,"MPG",Standardize=true);Check the model for convergence.
Mdl.ConvergenceInfo.Converged
ans = logical
1
The value 1 indicates that the model did converge.
To better understand the trained SVM model, visualize the linear kernel coefficients of the model. Note that the categorical predictor Origin is expanded into two separate predictors: Origin==USA and Origin==NotUSA.
[sortedCoefs,expandedIndex] = sort(Mdl.Beta,ComparisonMethod="abs"); sortedExpandedPreds = Mdl.ExpandedPredictorNames(expandedIndex); bar(sortedCoefs,Horizontal="on") yticklabels(strrep(sortedExpandedPreds,"_","\_")) xlabel("Linear Kernel Coefficient") title("Linear Kernel Coefficient per Predictor")

The Weight and Model_Year predictors have the greatest coefficient values, in terms of absolute value.
Compute the importance values of the predictors in Mdl by using the permutationImportance function. By default, the function uses 10 permutations to compute the mean and standard deviation of the importance values for each predictor in Mdl. For a fixed predictor and a fixed permutation of its values, the importance value is the difference in the loss due to the permutation of the values in the predictor. Because Mdl is a regression SVM model, permutationImportance uses the mean squared error (MSE) as the default loss function for computing importance values.
Importance = permutationImportance(Mdl,carsImportance)
Importance=7×3 table
Predictor ImportanceMean ImportanceStandardDeviation
______________ ______________ ___________________________
"Acceleration" 0.045464 0.11925
"Cylinders" 0.97081 0.30542
"Displacement" 1.4825 0.60587
"Horsepower" 0.85574 0.53354
"Model_Year" 13.696 1.8971
"Weight" 44.248 4.0521
"Origin" 3.8585 0.59796
Visualize the mean importance values.
[sortedImportance,index] = sort(Importance.ImportanceMean); sortedPreds = Importance.Predictor(index); bar(sortedImportance,Horizontal="on") yticklabels(strrep(sortedPreds,"_","\_")) xlabel("Mean Importance") title("Mean Importance per Predictor")

The Weight and Model_Year predictors have the greatest mean importance values. In general, the order of the predictors with respect to the mean importance matches the order of the predictors with respect to the absolute value of the linear kernel coefficients.
Compute the mean permutation predictor importance for the predictors in a classification neural network model. Calculate the per-class contributions to the predictor importance values.
Read the sample file CreditRating_Historical.dat into a table. The predictor data consists of financial ratios and industry sector information for a list of corporate customers. The response variable consists of credit ratings assigned by a rating agency. Preview the first few rows of the data set.
creditrating = readtable("CreditRating_Historical.dat");
head(creditrating) ID WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry Rating
_____ ______ ______ _______ ________ _____ ________ _______
62394 0.013 0.104 0.036 0.447 0.142 3 {'BB' }
48608 0.232 0.335 0.062 1.969 0.281 8 {'A' }
42444 0.311 0.367 0.074 1.935 0.366 1 {'A' }
48631 0.194 0.263 0.062 1.017 0.228 4 {'BBB'}
43768 0.121 0.413 0.057 3.647 0.466 12 {'AAA'}
39255 -0.117 -0.799 0.01 0.179 0.082 4 {'CCC'}
62236 0.087 0.158 0.049 0.816 0.324 2 {'BBB'}
39354 0.005 0.181 0.034 2.597 0.388 7 {'AA' }
Because each value in the ID variable is a unique customer ID, that is, length(unique(creditrating.ID)) is equal to the number of observations in creditrating, the ID variable is a poor predictor. Remove the ID variable from the table, and convert the Industry variable to a categorical variable.
creditrating = removevars(creditrating,"ID");
creditrating.Industry = categorical(creditrating.Industry);Convert the Rating response variable to a categorical variable.
creditrating.Rating = categorical(creditrating.Rating, ... ["AAA","AA","A","BBB","BB","B","CCC"]);
Partition the data into two sets. Use approximately 80% of the observations to train a neural network classifier, and 20% of the observations to compute predictor importance.
rng("default") % For reproducibility c = cvpartition(creditrating.Rating,"Holdout",0.20); creditTrain = creditrating(training(c),:); creditImportance= creditrating(test(c),:);
Train a neural network classifier by passing the training data creditTrain to the fitcnet function. Specify to standardize the numeric predictors. Change the relative gradient tolerance from 0.000001 (default) to 0.0005, so that the training process can stop earlier.
Mdl = fitcnet(creditTrain,"Rating",Standardize=true, ... GradientTolerance=5e-4);
Check the model for convergence.
Mdl.ConvergenceInfo.ConvergenceCriterion
ans = 'Relative gradient tolerance reached.'
The model stops training after reaching the relative gradient tolerance.
Compute the importance values of the predictors in Mdl by using the permutationImportance function. By default, the function uses 10 permutations to compute the mean and standard deviation of the importance values for each predictor in Mdl. For a fixed predictor and a fixed permutation of its values, the importance value is the difference in the loss due to the permutation of the values in the predictor. Because Mdl is a classification neural network model, permutationImportance uses the minimal expected misclassification cost as the default loss function for computing importance values.
Because Mdl is a multiclass classifier, additionally return the mean and standard deviation of the importance values per class for each predictor.
[Importance,~,ImportancePerClass] = ... permutationImportance(Mdl,creditImportance,"Rating")
Importance=6×3 table
Predictor ImportanceMean ImportanceStandardDeviation
__________ ______________ ___________________________
"WC_TA" 0.014269 0.0062836
"RE_TA" 0.18372 0.013911
"EBIT_TA" 0.030178 0.0068664
"MVE_BVTD" 0.55744 0.010545
"S_TA" 0.048892 0.010217
"Industry" 0.074682 0.011861
ImportancePerClass=6×3 table
Predictor ImportanceMean ImportanceStandardDeviation
__________ ____________________________________________________________________________________________ _________________________________________________________________________________________
AAA AA A BBB BB B CCC AAA AA A BBB BB B CCC
__________ __________ _________ __________ ________ __________ ___________ __________ _________ _________ _________ _________ _________ __________
"WC_TA" 0.0019072 1.0408e-18 0.0013986 0.0010172 0.010709 -0.0020343 0.0012715 0.00089906 0.0023214 0.0029637 0.002862 0.0029565 0.001818 0.00059937
"RE_TA" 0.020979 0.015003 0.026446 0.014876 0.045514 0.039034 0.021869 0.0034561 0.0059274 0.0041003 0.0057817 0.007721 0.0024749 0.00053609
"EBIT_TA" 0.00038144 -0.0021615 0.0055944 -0.0043229 0.016574 0.01424 -0.00012715 0.0010468 0.0019001 0.002824 0.0046116 0.0036557 0.0023824 0.00040207
"MVE_BVTD" 0.11812 0.066497 0.08684 0.12982 0.10837 0.040559 0.0072473 0.0037646 0.003978 0.0052269 0.0083364 0.0050996 0.0035179 0.0020806
"S_TA" -0.0016529 0.0036872 0.006103 0.018563 0.02537 -0.0091545 0.0059758 0.0019001 0.0020281 0.0037335 0.0041612 0.0037266 0.0041003 0.0012062
"Industry" 0.0012715 0.0054673 0.010935 0.027082 0.017594 0.011952 0.00038144 0.0021611 0.002616 0.0041612 0.0077002 0.0064951 0.0032938 0.0017006
Visualize the mean importance values.
bar(Importance.ImportanceMean,Horizontal="on") yticklabels(strrep(Importance.Predictor,"_","\_")) xlabel("Mean Importance") title("Mean Importance per Predictor")

The MVE_BVTD predictor has the greatest mean importance value. This value indicates that permuting the values of MVE_BVTD leads to an increase in the minimal expected misclassification cost of about 0.55 (on average).
Visualize the mean importance values by class.
bar(ImportancePerClass.ImportanceMean{:,:}, ...
"stacked",Horizontal="on")
legend(Mdl.ClassNames)
yticklabels(strrep(ImportancePerClass.Predictor,"_","\_"))
xlabel("Mean Importance")
title("Mean Importance per Predictor and Class")
Each segment indicates the mean importance value for the specified predictor and class. For example, the dark blue segment in the MVE_BVTD stacked bar indicates that the mean importance value for the MVE_BVTD predictor and the AAA class is slightly greater than 0.1. For each predictor, the sum of the segment values (including negative values) equals the mean predictor importance value.
Find the most important predictors in an SVM classifier by using the permutationImportance function. Use this subset of predictors to retrain the model. Ensure that the retrained model performs similarly to the original model on a test set.
This example uses the 1994 census data stored in census1994.mat. The data set consists of demographic information from the US Census Bureau that you can use to predict whether an individual makes over $50,000 per year.
Load the sample data census1994, which contains the training data adultdata and the test data adulttest. Preview the first few rows of the training data set.
load census1994
head(adultdata) age workClass fnlwgt education education_num marital_status occupation relationship race sex capital_gain capital_loss hours_per_week native_country salary
___ ________________ __________ _________ _____________ _____________________ _________________ _____________ _____ ______ ____________ ____________ ______________ ______________ ______
39 State-gov 77516 Bachelors 13 Never-married Adm-clerical Not-in-family White Male 2174 0 40 United-States <=50K
50 Self-emp-not-inc 83311 Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 0 0 13 United-States <=50K
38 Private 2.1565e+05 HS-grad 9 Divorced Handlers-cleaners Not-in-family White Male 0 0 40 United-States <=50K
53 Private 2.3472e+05 11th 7 Married-civ-spouse Handlers-cleaners Husband Black Male 0 0 40 United-States <=50K
28 Private 3.3841e+05 Bachelors 13 Married-civ-spouse Prof-specialty Wife Black Female 0 0 40 Cuba <=50K
37 Private 2.8458e+05 Masters 14 Married-civ-spouse Exec-managerial Wife White Female 0 0 40 United-States <=50K
49 Private 1.6019e+05 9th 5 Married-spouse-absent Other-service Not-in-family Black Female 0 0 16 Jamaica <=50K
52 Self-emp-not-inc 2.0964e+05 HS-grad 9 Married-civ-spouse Exec-managerial Husband White Male 0 0 45 United-States >50K
Each row contains the demographic information for one adult. The last column, salary, shows whether a person has a salary less than or equal to $50,000 per year or greater than $50,000 per year.
Combine the education_num and education variables in both the training and test data to create a single ordered categorical variable that shows each person's highest level of education.
edOrder = unique(adultdata.education_num,"stable"); edCats = unique(adultdata.education,"stable"); [~,edIdx] = sort(edOrder); adultdata.education = categorical(adultdata.education, ... edCats(edIdx),Ordinal=true); adultdata.education_num = []; adulttest.education = categorical(adulttest.education, ... edCats(edIdx),Ordinal=true); adulttest.education_num = [];
Split the training data further using a stratified holdout partition. Create a separate data set to compute predictor importance by permutation. Reserve approximately 30% of the observations to compute permutation predictor importance values, and use the rest of the observations to train a support vector machine (SVM) classifier.
rng("default") % For reproducibility c = cvpartition(adultdata.salary,"Holdout",0.30); tblTrain = adultdata(training(c),:); tblImportance = adultdata(test(c),:);
Train an SVM classifier by using the training set. Specify the salary column of tblTrain as the response and the fnlwgt column as the observation weights. Standardize the numeric predictors. Use a Gaussian kernel function to fit the model, and let fitcsvm select an appropriate kernel scale parameter.
Mdl = fitcsvm(tblTrain,"salary",Weights="fnlwgt", ... Standardize=true, ... KernelFunction="gaussian",KernelScale="auto");
Check the model for convergence.
Mdl.ConvergenceInfo.Converged
ans = logical
1
The value 1 indicates that the model did converge.
Compute the weighted classification error using the test set adulttest.
L = loss(Mdl,adulttest,"salary", ... Weights="fnlwgt")
L = 0.1428
Compute the importance values of the predictors in Mdl by using the permutationImportance function and the tblImportance data. By default, the function uses 10 permutations to compute the mean and standard deviation of the importance values for each predictor in Mdl. For a fixed predictor and a fixed permutation of its values, the importance value is the difference in the loss due to the permutation of the values in the predictor. Because Mdl is a classification SVM model and observation weights are specified, permutationImportance uses the weighted classification error as the default loss function for computing importance values.
Importance = ... permutationImportance(Mdl,tblImportance,"salary", ... Weights="fnlwgt")
Importance=12×3 table
Predictor ImportanceMean ImportanceStandardDeviation
________________ ______________ ___________________________
"age" 0.010551 0.0012799
"workClass" 0.0091527 0.0016168
"education" 0.032974 0.0040815
"marital_status" 0.014255 0.0017169
"occupation" 0.018887 0.0015031
"relationship" 0.0137 0.0012572
"race" -0.0012146 0.00055194
"sex" -6.7399e-05 0.00073437
"capital_gain" 0.027692 0.001089
"capital_loss" 0.0047455 0.00091375
"hours_per_week" 0.0062861 0.001831
"native_country" 0.00063405 0.00085922
Sort the predictors based on their mean importance values.
[sortedImportance,index] = sort(Importance.ImportanceMean, ... "descend"); sortedPreds = Importance.Predictor(index); bar(sortedImportance) xticklabels(strrep(sortedPreds,"_","\_")) ylabel("Mean Importance") title("Mean Importance per Predictor")

For model Mdl, the native_country, sex, and race predictors seem to have little effect on the prediction of a person's salary.
Retrain the SVM classifier using the nine most important predictors (and excluding the three least important predictors).
predSubset = sortedPreds(1:9)
predSubset = 9×1 string
"education"
"capital_gain"
"occupation"
"marital_status"
"relationship"
"age"
"workClass"
"hours_per_week"
"capital_loss"
newMdl = fitcsvm(tblTrain,"salary",Weights="fnlwgt", ... PredictorNames=predSubset,Standardize=true, ... KernelFunction="gaussian",KernelScale="auto");
Compute the weighted test set classification error using the retrained model.
newL = loss(newMdl,adulttest,"salary", ... Weights="fnlwgt")
newL = 0.1437
newMdl has almost the same test set loss as Mdl and uses fewer predictors.
Train a multiclass support vector machine (SVM). Find the predictors in the model with the greatest median permutation predictor importance.
Load the humanactivity data set. The data set contains 24,075 observations of five physical human activities: sitting, standing, walking, running, and dancing. Each observation has 60 features extracted from acceleration data measured by smartphone accelerometer sensors. Create the response variable activity using the actid and actnames variables.
load humanactivity
activity = categorical(actid,1:5,actnames);Partition the data into two sets. Use approximately 75% of the observations to train a multiclass SVM classifier, and 25% of the observations to compute predictor importance values.
rng("default") % For reproducibility c = cvpartition(activity,"Holdout",0.25); trainX = feat(training(c),:); trainY = activity(training(c)); importanceX = feat(test(c),:); importanceY = activity(test(c));
Train a multiclass SVM classifier by passing the training data trainX and trainY to the fitcecoc function.
Mdl = fitcecoc(trainX,trainY);
Compute the importance values of the predictors in Mdl by using the permutationImportance function. Return the importance value for each predictor and permutation.
[~,ImportancePerPermutation] = ...
permutationImportance(Mdl,importanceX,importanceY)ImportancePerPermutation=10×60 table
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34 x35 x36 x37 x38 x39 x40 x41 x42 x43 x44 x45 x46 x47 x48 x49 x50 x51 x52 x53 x54 x55 x56 x57 x58 x59 x60
_________ ________ __________ ________ ________ _________ __________ ___________ __________ _______ ________ _________ ________ __________ __________ __________ __________ ___________ ___________ _________ __________ __________ ___________ __________ __________ __________ _________ ___________ __________ ________ ___________ ___________ ___________ _________ _________ _________ ________ __________ ___________ __________ _________ ___________ ___________ __________ ___________ ___________ ___________ __________ _________ __________ ___________ ________ _______ __________ _______ _______ _________ _______ _______ ___________
0.0051499 0.042365 0.0018275 0.01063 0.063336 0.0023255 0.0018268 -0.00016589 0.0011631 0.17301 0.014453 0.0091398 0.062969 0.0011626 0.00049842 0.00016622 0.00083079 -0.00033228 0.00016614 0.001495 0.00049825 0.00083129 0.00033245 0.00049876 0.00083079 0.00049825 0.002326 2.5059e-07 0.0014948 0.018107 -8.353e-08 -0.0003322 -0.00033053 0.0023275 0.0044885 0.0038208 0.0103 0.0014938 -0.00016622 0.00016631 0.002824 0.00016698 0 0.0011637 0.00066448 -0.00049825 -0.00033228 0.00066456 0.00216 0.00099701 -0.0018275 0.073765 0.21449 0.00033245 0.22317 0.52111 0.0023256 0.14073 0.23433 -0.00016614
0.0056483 0.037878 0.0014945 0.011628 0.062671 0.0031565 0.0016609 0.00016622 0.00083079 0.17135 0.011628 0.0091399 0.066459 0.00099634 0.00099684 0.00066465 0.00049842 -0.00016614 8.353e-08 0.0019934 0.00049834 0.00099734 -0.00033228 0.00033253 0.00066456 0.0011627 0.0033229 2.5059e-07 0.0016609 0.019936 0.00049834 -0.00016606 -0.0021582 0.0016627 0.0046544 0.0019932 0.011796 0.002491 0.00016606 0.00033236 0.0011627 0.00049951 -0.00016606 0.0011635 0.00099676 -0.0011629 -0.0008307 0.00066456 0.00216 0.00083079 -0.0014953 0.075095 0.20917 0.00033236 0.22716 0.52128 0.003489 0.13624 0.23582 -0.00016614
0.0064791 0.042364 0.00066423 0.012624 0.062838 0.0043196 0.0021595 2.5059e-07 0.0013293 0.176 0.013622 0.0081426 0.061306 0.0013288 0.00066465 0.00033228 0.00066448 0 0.00066456 0.0016612 0.001329 0.00066506 -0.00033228 0.00049867 0.001163 0.001163 0.0028244 3.3412e-07 0.001661 0.017942 -0.00049859 -0.00033228 -0.00049642 0.0024937 0.0051529 0.0043193 0.011131 0.0021583 -8.353e-08 0.00033245 0.0023256 -0.00033136 -0.00033228 0.00033262 0.00066448 -0.00083062 -0.00033236 0.00066456 0.0018275 0.00066465 -0.0016614 0.069944 0.21349 0.00033236 0.22483 0.52161 0.0021596 0.13276 0.23067 -0.00016614
0.0041528 0.044856 0.0031563 0.013621 0.060178 0.0034886 0.0013286 -0.00033203 0.00099684 0.17384 0.013455 0.0078109 0.059312 0.0021595 0.00083079 0.00033236 0.0016614 0.00049851 0.00033228 0.0016612 0.0011631 0.0011637 0.00049851 0.00049876 0.001163 0.001329 0.0029908 2.5059e-07 0.0011624 0.020932 0.0003322 -0.00049834 0.00066682 0.0014965 0.0046546 0.0033226 0.011463 0.0021583 0.00016606 1.6706e-07 0.001661 -0.00082978 -0.00033228 0.0011634 0.00099668 -0.00049825 -0.00083087 0.00099701 0.002326 0.0008307 -0.0013291 0.073101 0.21515 0.00016631 0.23048 0.51862 0.0018275 0.13026 0.23034 0.00016614
0.0051503 0.040703 0.0029904 0.012791 0.063668 0.0041532 0.0013285 -0.00016606 0.00033228 0.16719 0.010797 0.0069799 0.060476 0.0019931 0.0011631 0.00016597 0.0018276 0.00016614 0.00033228 0.0011626 0.0016613 0.00066523 0.00033245 0.00033253 0.00099676 0.00099676 0.0029906 -0.00049817 0.0019936 0.020268 0.001163 -0.00016606 -0.0013272 0.0029922 0.0044885 0.0041531 0.010799 0.001826 -0.00016622 0.00016631 0.0014948 -0.00082995 -0.00016614 0.00066481 0.00049825 -0.00099668 -0.00083079 0.00066456 0.0023261 0.00033236 -0.00083062 0.069446 0.20452 0.00033236 0.22367 0.52577 0.0023254 0.13259 0.23167 -0.00016614
0.0048177 0.042032 0.0013287 0.010963 0.060843 0.0036546 0.00083003 -0.00049842 0.00099684 0.16487 0.015782 0.0064816 0.066624 0.00066381 0.001163 0.00049851 0.0014953 0.00033228 0.00033236 0.001329 0.00099676 0.00099743 -0.00016606 0.00066481 0.00066456 0.00083037 0.0029905 0.00049884 0.0016611 0.018772 0.00016597 -0.00049842 -0.0011614 0.0018289 0.0058175 0.0038207 0.010799 0.00049667 0.0003322 0.00016631 0.0021594 -0.00066406 0.00016622 0.00049867 0.00016589 -0.00033203 -0.00066456 0.00049842 0.0021599 0.00049842 -0.0016613 0.071439 0.20967 0.00033236 0.22616 0.5261 0.0031567 0.1414 0.23001 -0.00016614
0.0061466 0.044524 0.0016612 0.010797 0.064334 0.0029902 0.0013285 -0.00099684 0.00066456 0.17633 0.012626 0.0088077 0.062636 0.0026578 0.00049842 0.00016614 0.0016614 0.00049842 -0.00016614 0.001329 0.00033203 0.00049909 -0.00016597 0.00016639 0.00099684 0.00099668 0.0023259 -0.00033203 0.00083029 0.021431 0.00066456 -0.00016606 -0.0013274 0.0019949 0.0058172 0.0043194 0.011795 0.0016597 0.00049834 1.6706e-07 0.0024919 -0.00099618 -0.00033228 0.00099751 0.00083062 -0.00066448 -0.0008307 0.00033228 0.0018275 0.00033228 -0.0014953 0.073931 0.20635 0.00016622 0.23048 0.53075 0.0026581 0.13558 0.23317 -0.00016614
0.0056481 0.040038 0.0024918 0.011295 0.060677 0.0038211 0.0013287 0.00049867 0.00066456 0.17467 0.012791 0.006814 0.057984 0.0013285 0.0018275 0.00016614 0.001163 0.00033236 0.00049842 0.0016612 -8.353e-08 0.00083137 0.00016622 0.00066481 0.00099676 0.0011628 0.0033227 0.00033262 0.00066406 0.021431 0.00083079 8.353e-08 -0.00099526 0.0026598 0.0046546 0.0036545 0.010466 0.0011613 0.00016606 0 0.0019936 0.00049942 -0.00049842 0.00049884 0.00083062 -0.00099668 -0.00066456 0.00099693 0.0018277 0.00049842 -0.0016613 0.07011 0.20934 0.00049859 0.22799 0.52344 0.0026578 0.1379 0.23333 -0.00016614
0.0046506 0.045521 0.0029904 0.011295 0.062671 0.0034884 0.00082995 -0.00049834 0.001163 0.16869 0.012957 0.0089734 0.06031 0.001495 0.0008307 0.00016622 0.0013292 0.00016614 0.00033228 0.0018273 0.00083045 0.0014959 -0.00016606 0.00033253 0.00099676 0.0019937 0.0028243 0.00083095 0.0021595 0.017444 0.00016606 -0.00016606 -0.0016597 0.0016628 0.00615 0.0031563 0.010134 0.0026568 0.0003322 0.00016631 0.001495 -0.00082987 -0.00016614 0.00049859 -0.00016639 -0.00066431 -0.00049842 0.00066456 0.0013291 0.00049851 -0.0019936 0.076258 0.21432 0.00016631 0.22383 0.51895 0.0023256 0.13441 0.23998 -0.00016614
0.0064787 0.037878 0.0014949 0.010963 0.064831 0.0036547 0.0016609 -0.00083045 0.0008307 0.17966 0.012791 0.0099706 0.061972 0.0018271 0.00099693 0.00016614 0.0016615 0.00049842 0 0.0016611 0.00083054 0.00049901 0.00016631 0.00016639 0.0008307 0.0014953 0.0029904 0.00049867 0.0023256 0.01927 0.00066456 8.353e-08 -0.00066256 0.0026597 0.0054854 0.0039873 0.011796 0.0019925 0.0003322 0.00016631 0.0014948 -0.00083003 -0.00016614 0.00099743 0.0016612 -0.00083079 -0.00049842 0.00049842 0.0016613 0.00016614 -0.0016614 0.07443 0.21116 0.00033245 0.22018 0.52809 0.0019935 0.13226 0.23283 -0.00016614
ImportancePerPermutation is a table of 10-by-60 predictor importance values, where each entry corresponds to permutation i of predictor p.
Compute the median permutation predictor importance for each predictor.
medianImportance = median(ImportancePerPermutation)
medianImportance=1×60 table
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34 x35 x36 x37 x38 x39 x40 x41 x42 x43 x44 x45 x46 x47 x48 x49 x50 x51 x52 x53 x54 x55 x56 x57 x58 x59 x60
_________ ________ _________ ________ ________ _________ _________ ___________ __________ _______ ________ _________ ________ _________ __________ __________ _________ __________ __________ _________ __________ __________ __________ _________ __________ _________ _________ __________ _________ ________ __________ ___________ __________ _________ _________ _________ ________ _________ __________ __________ _________ ___________ ___________ __________ __________ ___________ ___________ __________ _________ __________ __________ ________ _______ __________ ______ _______ _________ _____ _____ ___________
0.0053992 0.042198 0.0017443 0.011295 0.062755 0.0035716 0.0013287 -0.00024904 0.00091381 0.17343 0.012874 0.0084752 0.061639 0.0014119 0.00091381 0.00016622 0.0014123 0.00024921 0.00033228 0.0016611 0.00083049 0.00083133 1.2529e-07 0.0004156 0.00099676 0.0011628 0.0029905 2.9235e-07 0.0016609 0.019603 0.00041527 -0.00016606 -0.0010783 0.0021612 0.0049038 0.0038208 0.010965 0.0019093 0.00016606 0.00016631 0.0018273 -0.00074692 -0.00016614 0.00083112 0.00074755 -0.00074755 -0.00066456 0.00066456 0.0019938 0.00049846 -0.0016613 0.073433 0.21042 0.00033236 0.2255 0.52253 0.0023256 0.135 0.233 -0.00016614
Plot the median predictor importance values. For reference, plot the line.
bar(medianImportance{1,:})
hold on
yline(0.05,"--")
hold off
xlabel("Predictor")
ylabel("Median Importance")
title("Median Importance per Predictor")
Only ten predictors have median predictor importance values that are greater than 0.05.
Compute the mean permutation predictor importance for the predictors in a discriminant analysis classifier. Use a loss function that corresponds to the error rate.
Load Fisher's iris data set. Determine the number of unique classes.
fishertable = readtable("fisheriris.csv");
K = length(unique(fishertable.Species));Create a default misclassification cost matrix where 0 corresponds to a correct classification and 1 corresponds to a misclassification.
Cost = ones(K) - eye(K)
Cost = 3×3
0 1 1
1 0 1
1 1 0
Train a discriminant analysis classifier using the entire data set and the cost matrix.
rng(0,"twister") % For reproducibility Mdl = fitcdiscr(fishertable,"Species",Cost=Cost);
Predict labels for the data set and return class scores.
[label,s,~] = predict(Mdl,fishertable);
Create a dummy variable matrix that contains the true classifications.
C = dummyvar(categorical(fishertable.Species));
Calculate the mean permutation predictor importance for the predictors using a loss function that does not use observation weights (shown at the end of this example). For each observation, the loss function applies misclassification costs to the classification score, and then finds the class with the highest score and compares it to the true class. The loss value is the fraction of misclassified observations (that is, the error rate).
Importance = permutationImportance(Mdl,lossFun=@ErrorRate);
Sort the predictors based on their mean importance values. Display a bar chart.
[sortedImportance,index] = sort(Importance.ImportanceMean); sortedPreds = Importance.Predictor(index); bar(sortedImportance,Horizontal="on") yticklabels(strrep(sortedPreds,"_","\_")) xlabel("Mean Importance") title("Mean Importance per Predictor")
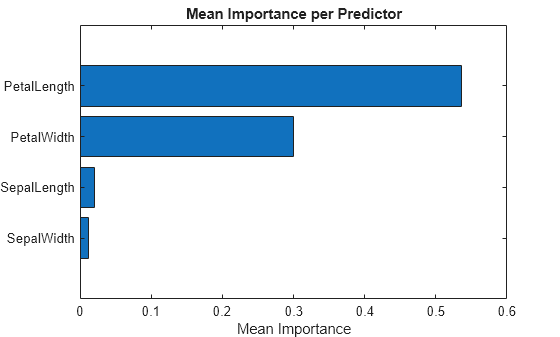
The PetalLength and PetalWidth predictors have the strongest influence on the model's predictions.
Error Rate Loss Function
This loss function returns a loss value that is equal to the fraction of misclassified observations (the error rate). The Classification Learner app uses this function when you create a permutation importance plot. If you specify a nondefault classification cost matrix, and the model is a k-nearest neighbor (KNN), discriminant analysis, or naive Bayes model, the app uses a modified version of this function that applies costs to scores.
function loss = ErrorRate(C, s, ~, Cost) % C is the N-by-K logical matrix for N observations and K classes % indicating the class to which the corresponding observation belongs. % The column order corresponds to the class order in Mdl.ClassNames. % s is the N-by-K matrix of predicted scores. % Cost is the K-by-K numeric matrix of misclassification costs. % % Uncomment the following line for k-nearest neighbor, discriminant analysis, % and naive Bayes models when you specify a nondefault cost matrix. % s = s*(-Cost); % Apply costs to scores. % % Find the class with the highest score for each observation. [~, predictedClass] = max(s, [], 2); % Find the true class for each observation. [~, trueClass] = max(C, [], 2); % Calculate the number of misclassified observations. misclassified = trueClass ~= predictedClass; % Calculate the unweighted classification error. loss = sum(misclassified) / length(misclassified); end
Input Arguments
Machine learning model, specified as a classification or regression model object, as
given in the following tables of supported models. If Mdl is a
compact model object, you must provide data for computing importance values.
Classification Model Objects
| Model | Full or Compact Classification Model Object |
|---|---|
| Discriminant analysis classifier | ClassificationDiscriminant, CompactClassificationDiscriminant |
| Multiclass model for support vector machines or other classifiers | ClassificationECOC, CompactClassificationECOC |
| Ensemble of learners for classification | ClassificationEnsemble, CompactClassificationEnsemble,
ClassificationBaggedEnsemble |
| Generalized additive model (GAM) | ClassificationGAM, CompactClassificationGAM |
| Gaussian kernel classification model using random feature expansion | ClassificationKernel |
| k-nearest neighbor classifier | ClassificationKNN |
| Linear classification model | ClassificationLinear |
| Multiclass naive Bayes model | ClassificationNaiveBayes, CompactClassificationNaiveBayes |
| Neural network classifier | ClassificationNeuralNetwork, CompactClassificationNeuralNetwork |
| Support vector machine (SVM) classifier for one-class and binary classification | ClassificationSVM, CompactClassificationSVM |
| Binary decision tree for multiclass classification | ClassificationTree, CompactClassificationTree |
Regression Model Objects
| Model | Full or Compact Regression Model Object |
|---|---|
| Ensemble of regression models | RegressionEnsemble, RegressionBaggedEnsemble, CompactRegressionEnsemble |
| Generalized additive model (GAM) | RegressionGAM, CompactRegressionGAM |
| Gaussian process regression | RegressionGP, CompactRegressionGP |
| Gaussian kernel regression model using random feature expansion | RegressionKernel |
| Linear regression for high-dimensional data | RegressionLinear |
| Neural network regression model | RegressionNeuralNetwork, CompactRegressionNeuralNetwork (permutationImportance
does not support neural network models with multiple response
variables.) |
| Support vector machine (SVM) regression | RegressionSVM, CompactRegressionSVM |
| Regression tree | RegressionTree, CompactRegressionTree |
Sample data, specified as a table. Each row of Tbl corresponds
to one observation, and each column corresponds to one predictor variable. Optionally,
Tbl can contain a column for the response variable and a column
for the observation weights. Tbl must contain all of the predictors
used to train Mdl. Multicolumn variables and cell arrays other than
cell arrays of character vectors are not allowed.
If
Tblcontains the response variable used to trainMdl, then you do not need to specifyResponseVarNameorY.If you train
Mdlusing sample data contained in a table, then the input data forpermutationImportancemust also be in a table.
Data Types: table
Response variable name, specified as the name of a variable in
Tbl. If Tbl contains the response variable
used to train Mdl, then you do not need to specify
ResponseVarName.
If you specify ResponseVarName, then you must specify it as a
character vector or string scalar. For example, if the response variable is stored as
Tbl.Y, then specify ResponseVarName as
"Y".
The response variable must be a numeric vector, logical vector, categorical vector, character array, string array, or cell array of character vectors. If the response variable is a character array, then each row of the character array must be a class label.
Data Types: char | string
Response variable, specified as a numeric vector, logical vector, categorical vector, character array, string array, or cell array of character vectors.
If
Mdlis a classification model, then the following must be true:The data type of
Ymust be the same as the data type ofMdl.ClassNames. (The software treats string arrays as cell arrays of character vectors.)The distinct classes in
Ymust be a subset ofMdl.ClassNames.If
Yis a character array, then each row of the character array must be a class label.
Data Types: single | double | logical | char | string | cell | categorical
Predictor data, specified as a numeric matrix. permutationImportance
assumes that each row of X corresponds to one observation, and each
column corresponds to one predictor variable.
X and Y must have the same number of
observations.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: permutationImportance(Tbl,"Y",PredictorsToPermute=["Pred1","Pred2","Pred3"],NumPermutations=15)
specifies to use 15 permutations to compute predictor importance values for the predictors
Pred1, Pred2, and Pred3 in table
Tbl.
Loss function, specified as a built-in loss function name or a function handle.
Classification Loss Functions
The following table lists the available loss functions for classification.
| Value | Description |
|---|---|
"binodeviance" | Binomial deviance |
"classifcost" | Observed misclassification cost |
"classiferror" | Misclassified rate in decimal |
"exponential" | Exponential loss |
"hinge" | Hinge loss |
"logit" | Logistic loss |
"mincost" | Minimal expected misclassification cost (for classification scores that are posterior probabilities) |
"quadratic" | Quadratic loss |
To specify a custom classification loss function, use function handle notation. Your function must have the form:
lossvalue = lossfun(C,S,W,Cost)
The output argument
lossvalueis a scalar value.You specify the function name (
lossfun).Cis an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs. n is the number of observations in the data, and K is the number of distinct classes. The column order corresponds to the class order inMdl.ClassNames. CreateCby settingC(p,q) = 1, if observationpis in classq, for each row. Set all other elements of rowpto0.Sis an n-by-K numeric matrix of classification scores. The column order corresponds to the class order inMdl.ClassNames.Sis a matrix of classification scores, similar to the output ofpredict.Wis an n-by-1 numeric vector of observation weights.Costis a K-by-K numeric matrix of misclassification costs. For example,Cost = ones(K) – eye(K)specifies a cost of0for correct classification and1for misclassification.
Regression Loss Functions
The following table lists the available loss functions for regression.
| Value | Description |
|---|---|
"mse" | Mean squared error |
"epsiloninsensitive" | Epsilon-insensitive loss |
To specify a custom regression loss function, use function handle notation. Your function must have the form:
lossvalue = lossfun(Y,Yfit,W)
The output argument
lossvalueis a scalar value.You specify the function name (
lossfun).Yis an n-by-1 numeric vector of observed response values, where n is the number of observations in the data.Yfitis an n-by-1 numeric vector of predicted response values calculated using the corresponding predictor values.Wis an n-by-1 numeric vector of observation weights.
The default loss function depends on the model Mdl. For more
information, see Loss Functions.
Example: LossFun="classifcost"
Example: LossFun="epsiloninsensitive"
Data Types: char | string | function_handle
Number of permutations used to compute the mean and standard deviation of the predictor importance values for each predictor, specified as a positive integer scalar.
Example: NumPermutations=20
Data Types: single | double
Options for computing in parallel and setting random streams, specified as a
structure. Create the Options structure using statset. This table lists the option fields and their
values.
| Field Name | Value | Default |
|---|---|---|
UseParallel | Set this value to true to run computations in
parallel. | false |
UseSubstreams | Set this value to To compute
reproducibly, set | false |
Streams | Specify this value as a RandStream object or
cell array of such objects. Use a single object except when the
UseParallel value is true
and the UseSubstreams value is
false. In that case, use a cell array that
has the same size as the parallel pool. | If you do not specify Streams, then
permutationImportance uses the default stream or
streams. |
Note
You need Parallel Computing Toolbox™ to run computations in parallel.
Example: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))
Data Types: struct
Predicted response value to use for observations with missing predictor values,
specified as "median", "mean",
"omitted", or a numeric scalar.
| Value | Description |
|---|---|
"median" | permutationImportance uses the median of the observed response
values in the training data as the predicted response value for observations
with missing predictor values. |
"mean" | permutationImportance uses the mean of the observed response
values in the training data as the predicted response value for observations
with missing predictor values. |
"omitted" | permutationImportance excludes observations with missing
predictor values from loss computations. |
| Numeric scalar | permutationImportance uses this value as the predicted
response value for observations with missing predictor values. |
If an observation is missing an observed response value or an observation weight,
then permutationImportance does not use the observation in loss
computations.
Note
This name-value argument is valid only for these types of regression models:
Gaussian process regression, kernel, linear, neural network, and support vector
machine. That is, you can specify this argument only when Mdl
is a RegressionGP, CompactRegressionGP,
RegressionKernel, RegressionLinear,
RegressionNeuralNetwork,
CompactRegressionNeuralNetwork, RegressionSVM,
or CompactRegressionSVM object.
Example: PredictionForMissingValue="omitted"
Data Types: single | double | char | string
List of predictors for which to compute importance values, specified as one of the values in this table.
| Value | Description |
|---|---|
| Positive integer vector | Each entry in the vector is an index value indicating to compute
importance values for the corresponding predictor. The index values are
between 1 and p, where p is the
number of predictors listed in
|
| Logical vector | A |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable for which
to compute importance values. The names must match the entries in
Mdl.PredictorNames. |
"all" | Compute importance values for all predictors. |
Example: PredictorsToPermute=[true true false
true]
Data Types: single | double | logical | char | string | cell
Observation weights, specified as a nonnegative numeric vector or the name of a
variable in Tbl. The software weights each observation in
X or Tbl with the corresponding value in
Weights. The length of Weights must equal
the number of observations in X or
Tbl.
If you specify the input data as a table Tbl, then
Weights can be the name of a variable in
Tbl that contains a numeric vector. In this case, you must
specify Weights as a character vector or string scalar. For
example, if the weights vector W is stored as
Tbl.W, then specify it as "W".
By default, Weights is ones(n,1), where
n is the number of observations in X or
Tbl.
If you supply weights and
Mdlis a classification model, thenpermutationImportanceuses the weighted classification loss to compute importance values, and normalizes the weights to sum to the value of the prior probability in the respective class.If you supply weights and
Mdlis a regression model, thenpermutationImportanceuses the weighted regression loss to compute importance values, and normalizes the weights to sum to 1.
Note
This name-value argument is valid only when you specify a data argument
(X or Tbl) and Mdl
supports observation weights. If you compute importance values using the data in
Mdl (Mdl.X and Mdl.Y),
then permutationImportance uses the weights in
Mdl.W.
Data Types: single | double | char | string
Output Arguments
Importance values for the permuted predictors, averaged over all permutations, returned as a table with these columns.
| Column Name | Description |
|---|---|
Predictor | Name of each permuted predictor. You can specify the predictors to
include by using the PredictorsToPermute name-value
argument. |
ImportanceMean | Mean of the importance values for each predictor across all permutations.
You can specify the number of permutations by using the
NumPermutations name-value argument. |
ImportanceStandardDeviation | Standard deviation of the importance values for each predictor across all
permutations. You can specify the number of permutations by using the
NumPermutations name-value argument. |
For more information on how permutationImportance computes
these values, see Permutation Predictor Importance.
Importance values per permutation, returned as a table. Each entry (i,p) corresponds to permutation i of predictor p.
You can specify the number of permutations by using the
NumPermutations name-value argument, and you can specify the
predictors to include by using the PredictorsToPermute name-value
argument.
Importance values per class, returned as a table with these columns.
| Column Name | Description |
|---|---|
Predictor | Name of each permuted predictor |
ImportanceMean | Subdivided into separate columns for each class in
Mdl.ClassNames. Each value is the mean of the importance
values in a specified class for a specified predictor, across all
permutations. |
ImportanceStandardDeviation | Subdivided into separate columns for each class in
Mdl.ClassNames. Each value is the standard deviation of
the importance values in a specified class for a specified predictor, across
all permutations. |
For more information on how permutationImportance computes
these values, see Permutation Predictor Importance per Class.
Algorithms
Permutation predictor importance values measure how influential a model's predictor variables are in predicting the response. The influence of a predictor increases with the value of this measure. If a predictor is influential in prediction, then permuting its values should affect the model loss. If a predictor is not influential, then permuting its values should have little to no effect on the model loss.
For a predictor p in the predictor data X
(specified by Mdl.X, X, or Tbl)
and a permutation π of the values in p, the
permutation predictor importance value Impp(π) is: .
L is the loss function specified by the
LossFunname-value argument.Mdl is the classification or regression model specified by
Mdl.Xp(π) is the predictor data X with the predictor p replaced by the permuted predictor p(π).
Y is the response variable (specified by
Mdl.Y,Y, orTbl.Y), and W is the vector of observation weights (specified byMdl.Wor theWeightsname-value argument).
By default, permutationImportance computes the mean of the predictor
importance values for each predictor. That is, for a predictor p, the
function computes , where Impp is the mean permutation predictor importance of p, and
Q is the number of permutations specified by the
NumPermutations name-value argument.
For classification models, you can compute the mean permutation predictor importance values per class. For class k and predictor p, the mean permutation predictor importance value Impk,p is , where the sets Xk, Yk, and Wk are reduced to the observations with true class label k. The weights Wk are normalized to sum up to the value of the prior probability in class k. For more information on the other variables, see Permutation Predictor Importance.
Note that , where K is the number of classes in
Mdl.ClassNames.
Built-in loss functions are available for the classification and regression models you
can specify using Mdl. For more information on which loss functions are
supported (and which function is selected by default), see the loss
object function for the model you are using.
Classification Loss Functions
| Model | Full or Compact Classification Model Object | loss Object Function |
|---|---|---|
| Discriminant analysis classifier | ClassificationDiscriminant, CompactClassificationDiscriminant | loss |
| Multiclass model for support vector machines or other classifiers | ClassificationECOC, CompactClassificationECOC | loss |
| Ensemble of learners for classification | ClassificationEnsemble, CompactClassificationEnsemble, ClassificationBaggedEnsemble | loss |
| Generalized additive model (GAM) | ClassificationGAM, CompactClassificationGAM | loss |
| Gaussian kernel classification model using random feature expansion | ClassificationKernel | loss |
| k-nearest neighbor classifier | ClassificationKNN | loss |
| Linear classification model | ClassificationLinear | loss |
| Multiclass naive Bayes model | ClassificationNaiveBayes, CompactClassificationNaiveBayes | loss |
| Neural network classifier | ClassificationNeuralNetwork, CompactClassificationNeuralNetwork | loss |
| Support vector machine (SVM) classifier for one-class and binary classification | ClassificationSVM, CompactClassificationSVM | loss |
| Binary decision tree for multiclass classification | ClassificationTree, CompactClassificationTree | loss |
Regression Loss Functions
| Model | Full or Compact Regression Model Object | loss Object Function |
|---|---|---|
| Ensemble of regression models | RegressionEnsemble, RegressionBaggedEnsemble, CompactRegressionEnsemble | loss |
| Generalized additive model (GAM) | RegressionGAM, CompactRegressionGAM | loss |
| Gaussian process regression | RegressionGP, CompactRegressionGP | loss |
| Gaussian kernel regression model using random feature expansion | RegressionKernel | loss |
| Linear regression for high-dimensional data | RegressionLinear | loss |
| Neural network regression model | RegressionNeuralNetwork, CompactRegressionNeuralNetwork | loss |
| Support vector machine (SVM) regression | RegressionSVM, CompactRegressionSVM | loss |
| Regression tree | RegressionTree, CompactRegressionTree | loss |
Extended Capabilities
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2024a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)