CompactDirectForecaster

Compact direct forecasting model

Since R2023b

Description

CompactDirectForecaster is a compact version of a DirectForecaster model object for direct forecasting. The compact model does not include the time series data (X and Y) used for training the full model. Therefore, you cannot perform some tasks, such as a cross-validation, using the compact model.

Creation

Create a CompactDirectForecaster object from a full DirectForecaster model object by using compact.

Properties

Data Properties

CategoricalPredictors — Indices of categorical exogenous predictors

positive integer vector | []

This property is read-only.

Indices of categorical exogenous predictors, specified as a positive integer vector. Each index value in CategoricalPredictors indicates that the corresponding exogenous predictor listed in PredictorNames is categorical. If none of the exogenous predictors are categorical, then this property is empty ([]).

Data Types: double

PredictorNames — Names of exogenous predictors

cell array of character vectors

This property is read-only.

Names of the exogenous predictors, specified as a cell array of character vectors. The order of the elements in PredictorNames corresponds to the order of the exogenous predictors in the data argument used to train the model.

Data Types: cell

ResponseName — Name of response variable

character vector

This property is read-only.

Name of the response variable, specified as a character vector.

Data Types: char

Forecasting Properties

Horizon — Future time steps at which to forecast

positive integer vector

This property is read-only.

Future time steps at which to forecast, specified as a positive integer vector. Learners contains a trained regression model for each horizon step. For example, if the Horizon value of a direct forecasting model Mdl is [1 3], then Mdl.Learners contains two regression models: one that forecasts at horizon step 1, and one that forecasts at horizon step 3.

Data Types: double

LeadingPredictorLags — Predictor lags used for preparing leading exogenous predictors

nonnegative integer vector | cell array of nonnegative integer vectors | []

This property is read-only.

Leading predictor lags used for preparing leading exogenous predictors, specified as a nonnegative integer vector or cell array of nonnegative integer vectors.

• If LeadingPredictorLags is a vector, then for each element i in the vector, the software shifts the leading exogenous predictors backward in time by i steps, relative to the horizon time step. The software uses the resulting features as predictors. When the LeadingPredictorLags value is 0, the software uses the unshifted leading predictors.

  For example, if the Horizon value of a direct forecasting model is 3 and the LeadingPredictorLags value is 0, then the software uses the unshifted leading predictor values at horizon step 3 as predictor values.

• If LeadingPredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for leading exogenous predictor i.

If no leading predictor lags are used, then this property is empty ([]).

Data Types: double | cell

LeadingPredictors — Indices of leading exogenous predictors

positive integer vector | []

This property is read-only.

Indices of the leading exogenous predictors, specified as a positive integer vector. Leading predictors are predictors for which future values are known. Each index value in LeadingPredictors indicates that the corresponding exogenous predictor listed in PredictorNames is leading. If no exogenous predictors are leading predictors, then this property is empty ([]).

Data Types: double

Learners — Compact regression models trained at different horizon steps

cell array of regression model objects

This property is read-only.

Compact regression models trained at different horizon steps, specified as a cell array of regression model objects. That is, for a direct forecasting model Mdl, the software trains the regression model Mdl.Learners{1} at horizon step Mdl.Horizon(1).

This table lists the possible compact regression models.

Regression Model Type	Model Object
Bagged or boosted ensemble of trees	CompactRegressionEnsemble
General additive model (GAM)	CompactRegressionGAM
Gaussian process regression (GPR)	CompactRegressionGP
Kernel model	RegressionKernel
Linear model	RegressionLinear
Support vector machine (SVM)	CompactRegressionSVM
Decision tree	CompactRegressionTree

Data Types: cell

MaxLag — Maximum lag value

nonnegative integer scalar

This property is read-only.

Maximum lag value, specified as a nonnegative integer scalar. The MaxLag value depends on the values in ResponseLags, PredictorLags, and LeadingPredictorLags. Specifically, the software computes the maximum lag as follows:

MaxLag = max([0,ResponseLags,PredictorLags, ...
    LeadingPredictorLags - min(Horizon) + 1])

Unlike response lags and nonleading predictor lags, leading predictor lags are relative to horizon time steps instead of the current time step.

Data Types: double

PredictorLags — Predictor lags used for preparing nonleading exogenous predictors

positive integer vector | cell array of positive integer vectors | []

This property is read-only.

Predictor lags used for preparing nonleading exogenous predictors, specified as a positive integer vector or cell array of positive integer vectors.

• If PredictorLags is a vector, then for each element i in the vector, the software shifts the nonleading exogenous predictors backward in time by i steps and uses the resulting features as predictors.

• If PredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for nonleading exogenous predictor i.

If no predictor lags are used, then this property is empty ([]).

Data Types: double | cell

ResponseLags — Response lags used for preparing predictors

positive integer vector | []

This property is read-only.

Response lags used for preparing predictors, specified as a positive integer vector. Each element in ResponseLags indicates the number of time steps by which to shift the response backward in time. The resulting feature is used as a predictor. If no response lags are used, then this property is empty ([]).

Data Types: double

Prepared Data Properties

PreparedCategoricalPredictors — Indices of prepared categorical predictors

positive integer vector | []

This property is read-only.

Indices of the prepared categorical predictors, specified as a positive integer vector. Each index value in PreparedCategoricalPredictors indicates that the corresponding predictor listed in PreparedPredictorNames is categorical. If no prepared predictors are categorical predictors, then this property is empty ([]).

Data Types: double

PreparedPredictorNames — Names of prepared predictors

cell array of character vectors

This property is read-only.

Names of the prepared predictors, specified as a cell array of character vectors. These prepared predictors include variables created from both the exogenous predictor variables and the response variable used to train the direct forecasting model. Not every predictor is used at every horizon step. To see which predictors are used at a specific horizon step, consult the PreparedPredictorsPerHorizon table.

Data Types: cell

PreparedPredictorsPerHorizon — Prepared predictors at each horizon step

table of logical values

This property is read-only.

Prepared predictors at each horizon step, specified as a table of logical values. Each row of the table corresponds to a horizon step, and each column of the table corresponds to a prepared predictor as listed in PreparedPredictorNames.

For a direct forecasting model Mdl, the logical value in row i and column j indicates whether the software uses prepared predictor Mdl.PreparedPredictorNames(j) at horizon step Mdl.Horizon(i). If the value is 1 (true), then the software uses the predictor. If the value is 0 (false), then the software does not use the predictor.

Data Types: table

PreparedResponseNames — Names of prepared responses at each horizon step

cell array of character vectors

This property is read-only.

Names of the prepared responses at each horizon step, specified as a cell array of character vectors. That is, element i of PreparedResponseNames is the name of the response variable at the horizon step specified by element i of Horizon.

For example, given a direct forecasting model Mdl, the name of the response variable at horizon step Mdl.Horizon(1), Mdl.PreparedResponseNames{1}, matches the response variable name used in the first regression model in Learners (Mdl.Learners{1}.ResponseName).

Data Types: cell

Object Functions

loss	Loss at each horizon step
predict	Predict response at time steps in observed test data
forecast	Forecast response at time steps beyond available data
preparedPredictors	Obtain prepared data used for training or testing in direct forecasting

Examples

Reduce Size of Direct Forecasting Model

Reduce the size of a full direct forecasting model by removing the training data from the model. You can use a compact model to improve memory efficiency.

Load the sample file TemperatureData.csv, which contains average daily temperatures from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

temperatures = readtable("TemperatureData.csv");
head(temperatures)

    Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4     

For this example, use a subset of the temperature data that omits the first 100 observations.

Tbl = temperatures(101:end,:);

Create a datetime variable t that contains the year, month, and day information for each observation in Tbl. Then, use t to convert Tbl into a timetable.

numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);
Tbl.Time = t;
Tbl = table2timetable(Tbl);

Plot the temperature values in Tbl over time.

plot(Tbl.Time,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

Create a full direct forecasting model by using the data in Tbl. Train the model using a decision tree learner. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.

Mdl = directforecaster(Tbl,"TemperatureF", ...
    Learner="tree", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)

Mdl = 
  DirectForecaster

                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: [2]
                 Learners: {[1x1 classreg.learning.regr.CompactRegressionTree]}
                   MaxLag: [7]
          NumObservations: [465]

Mdl is a DirectForecaster object. By default, the horizon is one step ahead. That is, Mdl predicts a value that is one step into the future.

Reduce the size of the model by using the compact object function.

compactMdl = compact(Mdl)

compactMdl = 
  CompactDirectForecaster

                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: [2]
                 Learners: {[1x1 classreg.learning.regr.CompactRegressionTree]}
                   MaxLag: [7]

compactMdl is a CompactDirectForecaster model object. compactMdl contains fewer properties than the full model Mdl.

Display the amount of memory used by each direct forecasting model.

whos("Mdl","compactMdl")

  Name            Size             Bytes  Class                                            Attributes

  Mdl             1x1             110401  timeseries.forecaster.DirectForecaster                     
  compactMdl      1x1              42541  timeseries.forecaster.CompactDirectForecaster              

The full model is larger than the compact model.

More About

Direct Forecasting

Direct forecasting is a forecasting technique that uses separate models to predict the response values at different future time steps (horizon steps). This technique differs from recursive forecasting, where one model is used to predict values at multiple horizon steps.

The software prepares the predictor data for each model and then uses the model to forecast at a particular horizon step.

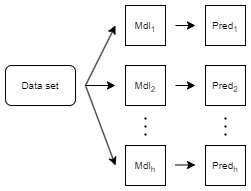
For more information, see PreparedPredictorsPerHorizon and Horizon.

Forecasting Data

The directforecaster function accepts data sets with regularly sampled values that include a response variable and exogenous predictors (optional). That is, the time steps between consecutive observations are the same. In this context, exogenous predictors are predictors that are not derived from the response variable.

Consider the following data set.

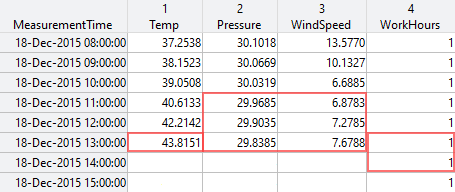
In this example, the row times in MeasurementTime show that the time difference between consecutive observations is one hour. The times 18-Dec-2015 14:00:00 and 18-Dec-2015 15:00:00 are future time steps that exist beyond the available data. They represent the first and second horizon steps. (See Horizon.)

Suppose the Temp variable is the response variable. The Pressure, WindSpeed, and WorkHours variables are exogenous predictors. The WorkHours variable is a leading exogenous predictor because its future values are known. (See LeadingPredictors.)

Before fitting a forecasting model, the software creates time-shifted features from the response and exogenous predictors based on user-specified lag values. In this example, the red rectangles indicate a ResponseLags value of 1, PredictorLags value of [1 2 3], and LeadingPredictorLags value of [0 1] at horizon step 1 (18-Dec-2015 14:00:00).

Version History

Introduced in R2023b