802.11ac Transmit Beamforming

Open Live Script

This example shows how to improve the performance of an IEEE® 802.11ac™ (Wi-Fi 5) link by beamforming the transmission when channel state information is available at the transmitter.

Introduction

Transmit beamforming focuses energy towards a receiver to improve the SNR of a link. In this scheme the transmitter is called a beamformer and the receiver is called a beamformee. A steering matrix is used by the beamformer to direct the energy to the beamformee. The steering matrix is calculated using channel state information obtained through channel measurements. In IEEE 802.11ac [ 1 ] these measurements are obtained by sounding the channel between beamformer and beamformee. To sound the channel the beamformer sends a null data packet (NDP) to the beamformee. The beamformee uses the channel information provided by sounding to calculate a feedback matrix. This matrix is fed back to the beamformer in a compressed format. The beamformer can then use the feedback matrix to create a steering matrix and beamform transmissions to the beamformee. The process of forming the steering matrix is shown in this diagram.

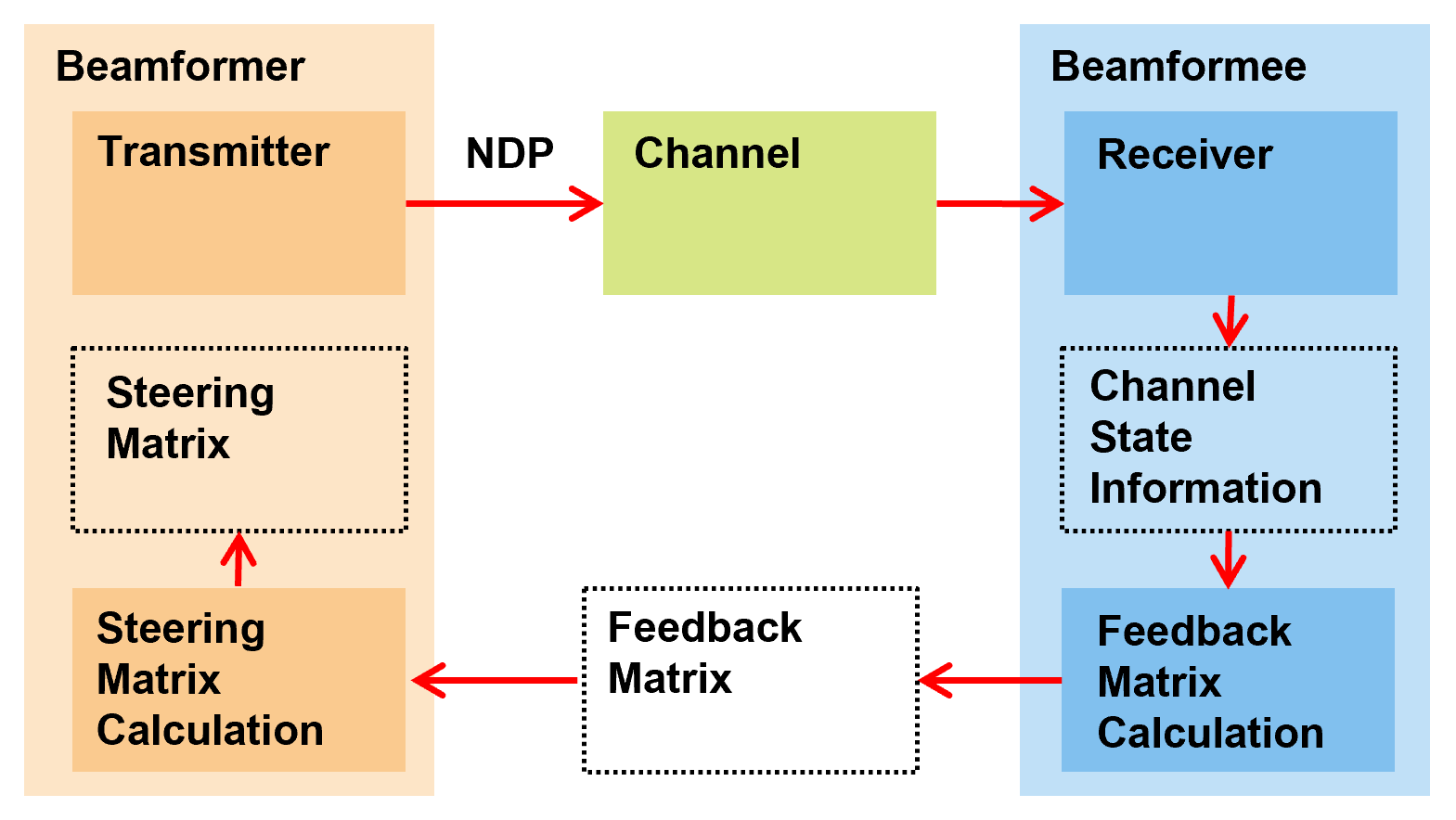
In IEEE 802.11ac the single user beamformee capability is not mandatory. Therefore, a multi-antenna transmitter may have to use a different scheme to transmit packets to a receiver which cannot act as a beamformee. One such scheme is spatial expansion. Spatial expansion allows space-time streams to be transmitted on a greater number of transmit antennas. Using spatial expansion can provide a small transmit diversity gain in channels with flat fading when compared to directly mapping space-time streams to transmit antennas [ 2 ].

This example demonstrates the benefits of transmit beamforming for a 4x2 MIMO configuration between a transmitter and receiver, with two space-time streams. First, the example demonstrates the operation of a receiver which is not capable of being a beamformee by measuring the signal quality of a transmission made using spatial expansion. To show the benefits of transmit beamforming the example measures the signal quality of a transmission over the same channel realization using transmit beamforming and compares the performance of the two schemes. The stages are shown in the diagram below.

Waveform Configuration

This examples simulates a 4x2 MIMO configuration with 2 space-time streams.

NumTxAnts = 4;  % Number of transmit antennas
NumSTS = 2;     % Number of space-time streams
NumRxAnts = 2;  % Number of receive antennas

The format specific configuration of a VHT waveform is described using a VHT format configuration object. Configure the waveform with a 20 MHz bandwidth and the MIMO configuration specified above.

cfgVHT = wlanVHTConfig;
cfgVHT.ChannelBandwidth = 'CBW20';
cfgVHT.APEPLength = 4000;
cfgVHT.NumTransmitAntennas = NumTxAnts;
cfgVHT.NumSpaceTimeStreams = NumSTS;
cfgVHT.MCS = 4; % 16-QAM, rate 3/4

Channel Configuration

This example uses a TGac channel model with delay profile Model-B. The channel realization is controlled with a seed to allow repeatability.

tgacChannel = wlanTGacChannel;
tgacChannel.DelayProfile = 'Model-B';
tgacChannel.ChannelBandwidth = cfgVHT.ChannelBandwidth;
tgacChannel.SampleRate = wlanSampleRate(cfgVHT);
tgacChannel.NumReceiveAntennas = NumRxAnts;
tgacChannel.NumTransmitAntennas = NumTxAnts;
tgacChannel.TransmitReceiveDistance = 100; % Meters
tgacChannel.RandomStream = 'mt19937ar with seed';
tgacChannel.Seed = 70; % Seed to allow repeatability

Noise is added to the time domain waveform at the output of the channel with a power, noisePower.

noisePower = -37; % dBW

Setup other objects and variables for simulation.

% Indices for extracting fields
ind = wlanFieldIndices(cfgVHT);

% AWGN channel to add noise with a specified noise power. The random
% process controlling noise generation is seeded to allow repeatability.
awgnChannel = comm.AWGNChannel;
awgnChannel.RandomStream = 'mt19937ar with seed';
awgnChannel.Seed = 5;
awgnChannel.NoiseMethod = 'Variance';
awgnChannel.Variance = 10^(noisePower/10);

% Calculate the expected noise variance after OFDM demodulation
noiseVar = vhtBeamformingNoiseVariance(noisePower,cfgVHT);

% Number of spatial streams
Nss = NumSTS/(cfgVHT.STBC+1);

% Get the number of occupied subcarriers in VHT fields
ofdmInfo = wlanVHTOFDMInfo('VHT-Data',cfgVHT);
Nst = ofdmInfo.NumTones;

% Generate a random PSDU which will be transmitted
rng(0); % Set random state for repeatability
psdu = randi([0 1],cfgVHT.PSDULength*8,1);

Transmission with Spatial Expansion

First perform a transmission using spatial expansion. This type of transmission may be made by a multi-antenna transmitter to a receiver which is not capable of being a beamformee. The SpatialMapping property of the format configuration object allows different spatial mapping schemes to be selected. This example uses the example spatial expansion matrix provided in Section 19.3.11.1.1.2 of [ 1 ]. Therefore, configure a 'Custom' spatial mapping. Use the custom spatial mapping matrix by assigning the SpatialMappingMatrix of the format configuration object. This matrix describes the mapping of each subcarrier for each space-time stream to all transmit antennas. Therefore the size of the spatial mapping matrix used is Nst-by-Nsts-by-Nt. Nst is the number of occupied subcarriers, Nsts is the number of space-time streams, and Nt is the number of transmit antennas. The spatial mapping matrix duplicates some of the space-time streams to form the desired number of transmit streams.

% Configure a spatial expansion transmission
vhtSE = cfgVHT;
vhtSE.SpatialMapping = 'Custom'; % Use custom spatial expansion matrix
vhtSE.SpatialMappingMatrix = helperSpatialExpansionMatrix(vhtSE);

% Generate waveform
tx = wlanWaveformGenerator(psdu,vhtSE);

% Pass waveform through a fading channel and add noise. Trailing zeros
% are added to allow for channel filter delay.
rx = tgacChannel([tx; zeros(15,NumTxAnts)]);
% Allow same channel realization to be used subsequently
reset(tgacChannel); 
rx = awgnChannel(rx);
% Allow same noise realization to be used subsequently
reset(awgnChannel);

% Estimate symbol timing
tOff = wlanSymbolTimingEstimate(rx(ind.LSTF(1):ind.LSIG(2),:),vhtSE.ChannelBandwidth);

% Channel estimation
vhtltf = rx(tOff+(ind.VHTLTF(1):ind.VHTLTF(2)),:);
vhtltfDemod = wlanVHTLTFDemodulate(vhtltf,vhtSE);
chanEstSE = wlanVHTLTFChannelEstimate(vhtltfDemod,vhtSE);

Demodulate and equalize the data field to recover OFDM symbols for each spatial stream.

vhtdata = rx(tOff+(ind.VHTData(1):ind.VHTData(2)),:);
[~,~,symSE] = wlanVHTDataRecover(vhtdata,chanEstSE,noiseVar,vhtSE,...
    'PilotPhaseTracking','None');

Plot the constellation of each spatial stream.

refSym = wlanReferenceSymbols(cfgVHT); % Reference constellation
seConst = vhtBeamformingPlotConstellation(symSE,refSym, ...
    'Spatial Expansion Transmission Equalized Symbols');

The variance in the constellation is approximately the same for each spatial stream as the SNRs are approximately the same. This is because the average power in the channel is on average approximately the same per space-time stream:

disp('Mean received channel power per space-time stream with spatial expansion: ')

Mean received channel power per space-time stream with spatial expansion:

for i = 1:NumSTS
    fprintf('  Space-time stream %d: %2.2f W\n',i, ...
        sum(mean(chanEstSE(:,i,:).*conj(chanEstSE(:,i,:)),1),3))
end

  Space-time stream 1: 0.73 W
  Space-time stream 2: 0.50 W

Transmission with Beamforming

When the receiver is capable of being a beamformee, a beamformed transmission can create a higher SNR compared to spatial expansion. This example demonstrates the advantage of having channel state information available to create and use a steering matrix.

Calculate a beamforming steering matrix, by passing an NDP through the channel. Use 'Direct' spatial mapping for the NDP transmission with the number of space-time streams is configured to match the number of transmit antennas. This uses the VHT-LTF to sound channels between each of the transmit antennas and receive antennas. Use the calculated beamforming matrix to beamform a transmission through the channel. The same channel realization is used for sounding and data transmission and there is no feedback compression between beamformee and beamformer, therefore the beamforming is regarded as perfect in this example.

% Configure a sounding packet
vhtSound = cfgVHT;
vhtSound.APEPLength = 0; % NDP so no data
vhtSound.NumSpaceTimeStreams = NumTxAnts;
vhtSound.SpatialMapping = 'Direct'; % Each TxAnt carries a STS

% Generate sounding waveform
soundingPSDU = [];
tx = wlanWaveformGenerator(soundingPSDU,vhtSound);

% Pass sounding waveform through the channel and add noise. Trailing zeros
% are added to allow for channel filter delay.
rx = tgacChannel([tx; zeros(15,NumTxAnts)]);
% Allow same channel realization to be used subsequently
reset(tgacChannel); 
rx = awgnChannel(rx);
% Allow same noise realization to be used subsequently
reset(awgnChannel);

% Estimate symbol timing
tOff = wlanSymbolTimingEstimate(rx(ind.LSTF(1):ind.LSIG(2),:),vhtSound.ChannelBandwidth);

Perform channel estimation using the sounding packet to estimate the actual channel response between each transmit and receive antenna.

% Channel estimation
vhtLLTFInd = wlanFieldIndices(vhtSound,'VHT-LTF');
vhtltf = rx(tOff+(vhtLLTFInd(1):vhtLLTFInd(2)),:);
vhtltfDemod = wlanVHTLTFDemodulate(vhtltf,vhtSound);
chanEstSound = wlanVHTLTFChannelEstimate(vhtltfDemod,vhtSound);

The channel estimated using the wlanVHTLTFChannelEstimate function includes cyclic shifts applied at the transmitter to each space-time stream. Remove the cyclic shifts applied at the transmitter from the channel estimate to calculate a beamforming steering matrix.

chanEstSound = vhtBeamformingRemoveCSD(chanEstSound, ...
    vhtSound.ChannelBandwidth,vhtSound.NumSpaceTimeStreams);

This example calculates the beamforming steering matrix using singular value decomposition (SVD). The SVD of the channel matrix results in two unitary matrices, U and V, and a diagonal matrix of singular values S. The first NumSTS columns of V per subcarrier are used as the beamforming steering matrix. The SVD is computed using the svd function.

chanEstPerm = permute(chanEstSound,[3 2 1]); % Permute to Nr-by-Nt-by-Nst
[U,S,V] = pagesvd(chanEstPerm,'econ');
steeringMatrix = permute(V(:,1:NumSTS,:),[3 2 1]); % Permute to Nst-by-Nsts-by-Nt

Apply the beamforming steering matrix calculated above as a custom spatial mapping matrix and use it to send data through the same channel.

% Configure a transmission with beamforming
vhtBF = cfgVHT;
vhtBF.SpatialMapping = 'Custom';
vhtBF.SpatialMappingMatrix = steeringMatrix; 

% Generate beamformed data transmission
tx = wlanWaveformGenerator(psdu,vhtBF);

% Pass through the channel and add noise. Trailing zeros
% are added to allow for channel filter delay.
rx = tgacChannel([tx; zeros(15,NumTxAnts)]);
rx = awgnChannel(rx);

% Estimate symbol timing
tOff = wlanSymbolTimingEstimate(rx(ind.LSTF(1):ind.LSIG(2),:),vhtBF.ChannelBandwidth);

% Channel estimation
vhtltf = rx(tOff+(ind.VHTLTF(1):ind.VHTLTF(2)),:);
vhtltfDemod = wlanVHTLTFDemodulate(vhtltf,vhtBF);
chanEstBF = wlanVHTLTFChannelEstimate(vhtltfDemod,vhtBF);

Demodulate and equalize the received data field to recover OFDM symbols for each spatial stream.

vhtdata = rx(tOff+(ind.VHTData(1):ind.VHTData(2)),:);
[~,~,symBF] = wlanVHTDataRecover(vhtdata,chanEstBF,noiseVar,vhtBF,...
    'PilotPhaseTracking','None','LDPCDecodingMethod','norm-min-sum');

Plot the equalized constellation for each spatial stream. The higher-order spatial stream has a larger variance. This is due to the ordered singular values of the channels used in SVD beamforming.

bfConst = vhtBeamformingPlotConstellation(symBF,refSym, ...
    'Beamformed Transmission Equalized Symbols');

This ordering is also visible in the average power of the received space-time streams. The power of the received first space-time stream is larger than the second space-time stream. This is because the received signal strength is a function of the singular values of the channel which SVD orders in a decreasing fashion.

disp('Mean received channel power per space-time stream with SVD transmit beamforming: ')

Mean received channel power per space-time stream with SVD transmit beamforming:

for i = 1:NumSTS
    fprintf('  Space-time stream %d: %2.2f W\n',i, ...
        sum(mean(chanEstBF(:,i,:).*conj(chanEstBF(:,i,:)),1),3))
end

  Space-time stream 1: 2.08 W
  Space-time stream 2: 0.45 W

Comparison and Conclusion

Plot the equalized constellation from the spatial expansion and beamformed transmissions for all spatial streams. Note the improved constellation using SVD-based transmit beamforming.

str = sprintf('%dx%d',NumTxAnts,NumRxAnts);
compConst = vhtBeamformingPlotConstellation([symSE(:) symBF(:)],refSym, ...
    'Beamformed Transmission Equalized Symbols', ...
    {[str ' Spatial Expansion'],[str ' Transmit Beamforming']});

Measure the improvement using the RMS and maximum error vector magnitude (EVM). EVM is a measure of demodulated signal quality.

EVM = comm.EVM;
EVM.AveragingDimensions = [1 2]; % Average over all subcarriers and symbols
EVM.MaximumEVMOutputPort = true;
EVM.ReferenceSignalSource  = 'Estimated from reference constellation';
EVM.ReferenceConstellation = refSym;

[rmsEVMSE,maxEVMSE] = EVM(symSE); % EVM using spatial expansion
[rmsEVMBF,maxEVMBF] = EVM(symBF); % EVM using beamforming

for i = 1:Nss
    fprintf(['Spatial stream %d EVM:\n' ...
        '  Spatial expansion:    %2.1f%% RMS, %2.1f%% max\n' ...
        '  Transmit beamforming: %2.1f%% RMS, %2.1f%% max\n'], ...
        i,rmsEVMSE(i),maxEVMSE(i),rmsEVMBF(i),maxEVMBF(i));
end

Spatial stream 1 EVM:
  Spatial expansion:    9.2% RMS, 44.8% max
  Transmit beamforming: 2.0% RMS, 8.6% max
Spatial stream 2 EVM:
  Spatial expansion:    9.2% RMS, 52.3% max
  Transmit beamforming: 4.1% RMS, 12.7% max

This example demonstrates that if a receiver is capable of being a beamformee, the SNR can potentially be improved when a transmission is beamformed compared to a spatial expansion transmission. The increase in received power when using beamforming can lead to more reliable demodulation or potentially even a higher order modulation and coding scheme to be used for the transmission.

In a realistic operational simulation the performance of beamforming would be degraded due to the delay between channel state information calculation and feedback by the beamformee and feedback quantization. For more information, see [ 2 ].

References

IEEE Std 802.11™-2020 IEEE Standard for Information technology - Telecommunications and information exchange between systems - Local and metropolitan area networks - Specific requirements - Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications.
Perahia, Eldad, and Robert Stacey. Next Generation Wireless LANS: 802.11n and 802.11ac. Cambridge University Press, 2013.