Modelli lineari (LTI)
Che cos’è un impianto?
Normalmente, gli ingegneri di controllo iniziano dallo sviluppo di una descrizione matematica del sistema dinamico che desiderano controllare. Il sistema da controllare è detto impianto. Come esempio di impianto, questa sezione usa un motore CC. Questa sezione sviluppa le equazioni differenziali che descrivono le proprietà elettromeccaniche di un motore CC con un carico inerziale. Successivamente, mostra come utilizzare le funzioni del Control System Toolbox™ per costruire modelli lineari basati su queste equazioni.
Rappresentazioni di modelli lineari
È possibile utilizzare le funzioni di Control System Toolbox per creare le seguenti rappresentazioni del modello:
Modelli stato-spazio (SS) di forma
dove A, B, C e D sono matrici di dimensioni appropriate, x è il vettore dello stato, mentre u e y sono i vettori di input e di output.
Funzioni di trasferimento (TF), ad esempio,
Modelli zero-poli-guadagno (ZPK), ad esempio,
Modelli con dati della risposta in frequenza (FRD), che consistono di misure campionate della risposta in frequenza di un sistema. Ad esempio, è possibile salvare i dati della risposta in frequenza raccolti in sede sperimentale all’interno di un modello FRD.
Nota
La progettazione di modelli RFD è un argomento specializzato che non viene trattato in questa sezione. Vedere Frequency Response Data (FRD) Models per una spiegazione dell’argomento.
Esempio SISO: Il motore CC
Un semplice modello di un motore CC con un carico inerziale mostra la velocità angolare del carico, , come output e la tensione applicata, , come input. L’obiettivo ultimo di questo esempio è di controllare la velocità angolare variando la tensione applicata. Questa figura mostra un semplice modello del motore CC.
Un semplice modello di motore CC con carico inerziale
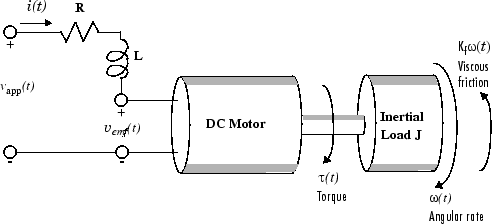
In questo modello, le dinamiche del motore stesso sono idealizzate: ad esempio, si assume che il campo magnetico sia costante. La resistenza del circuito è denotata da R e l’auto-induttanza dell’armatura da L. Se non si ha dimestichezza con le nozioni di base della modellazione dei motori CC, consultare un qualsiasi testo base sulla modellazione fisica. Con questo semplice modello e le leggi fondamentali della fisica è possibile sviluppare delle equazioni differenziali in grado di descrivere il comportamento di questo sistema elettromeccanico. In questo esempio, i rapporti tra potenziale elettrico e forza meccanica sono la legge di Faraday dell’induzione e la legge di Ampère per la forza di un conduttore che si muove attraverso un campo magnetico.
Derivazione matematica
La coppia osservata sull’asse del motore è proporzionale alla corrente i indotta dalla tensione applicata,
dove Km, la costante di armatura, è correlata alle proprietà fisiche del motore, come l’intensità del campo magnetico, il numero di avvolgimento del filo attorno alla bobina del conduttore, e così via. La forza controelettromotrice (indotta), , è una tensione proporzionale alla velocità angolare osservata sull’asse,
dove Kb, la costante emf, dipende anche da certe proprietà fisiche del sistema.
La parte meccanica delle equazioni del motore deriva dalla legge di Newton, secondo cui il carico inerziale J moltiplicato per la derivata della velocità angolare è pari alla somma di tutte le coppie intorno all’asse del motore. Il risultato è questa equazione,
dove è un’approssimazione lineare per l’attrito viscoso.
Infine, la parte elettrica delle equazioni del motore può essere descritta da
oppure, risolvendo per la tensione applicata e sostituendola alla forza controelettromotrice emf,
Questa sequenza di equazioni porta ad un insieme di due equazioni differenziali che descrivono il comportamento del motore, la prima per la corrente indotta,
e la seconda per la velocità angolare risultante,
Equazioni stato-spazio per il motore CC
Date le due equazioni differenziali derivate dall’ultima sezione, ora è possibile sviluppare una rappresentazione stato-spazio del motore CC come sistema dinamico. La corrente i e la velocità angolare ω sono i due stati del sistema. La tensione applicata, , è l’input del sistema, mentre la velocità angolare ω è l’output.
Rappresentazione stato-spazio dell’esempio di motore CC
Costruzione di modelli SISO
Una volta sviluppato un set di equazioni differenziali che descrivono il proprio impianto, è possibile costruire dei modelli SISO tramite semplici comandi. La seguente sezione tratta i seguenti argomenti
Costruzione di un modello stato-spazio del motore CC
Conversione tra diverse rappresentazioni del modello
Creazione di modelli a funzione di trasferimento e zero/poli/guadagno
Costruzione di un modello stato-spazio del motore CC
Inserire i seguenti valori nominali per i vari parametri di un motore CC.
R= 2.0 % Ohms L= 0.5 % Henrys Km = .015 % torque constant Kb = .015 % emf constant Kf = 0.2 % Nms J= 0.02 % kg.m^2
Dati questi valori, è possibile costruire la rappresentazione stato-spazio numerica utilizzando la funzione ss.
A = [-R/L -Kb/L; Km/J -Kf/J] B = [1/L; 0]; C = [0 1]; D = [0]; sys_dc = ss(A,B,C,D)
Questi comandi restituiscono il seguente risultato:
a =
x1 x2
x1 -4 -0.03
x2 0.75 -10
b =
u1
x1 2
x2 0
c =
x1 x2
y1 0 1
d =
u1
y1 0
Conversione tra diverse rappresentazioni del modello
Ora che si dispone di una rappresentazione stato-spazio del motore CC, è possibile effettuare la conversione in altre rappresentazioni del modello, compresi i modelli TF (funzione di trasferimento) e ZPK (zero/poli/guadagno).
Rappresentazione come funzione di trasferimento. È possibile utilizzare tf per convertire la rappresentazione stato-spazio nella funzione di trasferimento. Ad esempio, utilizzare questo codice per eseguire la conversione nella rappresentazione del motore DC come funzione di trasferimento.
sys_tf = tf(sys_dc)
Transfer function:
1.5
------------------
s^2 + 14 s + 40.02
Rappresentazione Zero/Poli/Guadagno. Analogamente, la funzione zpk esegue la conversione da una rappresentazione in formato stato-spazio o funzione di trasferimento al formato zero/poli/guadagno. Utilizzare questo codice per convertire la rappresentazione stato-spazio nella forma zero/poli/guadagno per il motore CC.
sys_zpk = zpk(sys_dc)
Zero/pole/gain:
1.5
-------------------
(s+4.004) (s+9.996)
Nota
La rappresentazione stato-spazio è la più adatta per i calcoli numerici. Per la massima accuratezza, eseguire la conversione nel formato stato-spazio prima di combinare i modelli ed evitare le rappresentazioni in formato funzione di trasferimento e zero/poli/guadagno, tranne per la specifica e l’ispezione del modello.
Creazione di modelli a funzione di trasferimento e zero/poli/guadagno
Nell’esempio del motore CC, l’approccio stato-spazio produce un set di matrici che rappresenta il modello. Se si sceglie un approccio diverso, è possibile costruire i modelli corrispondenti tramite tf, zpk, ss o frd.
sys = tf(num,den) % Transfer function sys = zpk(z,p,k) % Zero/pole/gain sys = ss(a,b,c,d) % State-space sys = frd(response,frequencies) % Frequency response data
Ad esempio, si può creare la funzione di trasferimento specificando con questo codice il numeratore e il denominatore.
sys_tf = tf(1.5,[1 14 40.02])
Transfer function:
1.5
------------------
s^2 + 14 s + 40.02
In alternativa, se si desidera creare la funzione di trasferimento del motore CC direttamente, utilizzare questi comandi.
s = tf('s');
sys_tf = 1.5/(s^2+14*s+40.02)
Questi comandi portano a questa funzione di trasferimento.
Transfer function:
1.5
--------------------
s^2 + 14 s + 40.02
Per costruire il modello in formato zero/poli/guadagno, utilizzare questo comando.
sys_zpk = zpk([],[-9.996 -4.004], 1.5)
Questo comando restituisce la seguente rappresentazione zero/poli/guadagno.
Zero/pole/gain:
1.5
-------------------
(s+9.996) (s+4.004)
Costruzione di sistemi a tempo discreto
Il software Control System Toolbox fornisce un supporto completo per i sistemi a tempo discreto. È possibile creare sistemi discreti nello stesso modo in cui si creano sistemi analogici; l’unica differenza è che bisogna specificare un periodo temporale campione per qualunque modello che si costruisce. Ad esempio,
sys_disc = tf(1, [1 1], .01);
crea un modello SISO nel formato funzione di trasferimento.
Transfer function: 1 ----- z + 1 Sample time: 0.01
Aggiunta di ritardi temporali ai modelli a tempo discreto
È possibile aggiungere ritardi temporali ai modelli a tempo discreto specificando un ritardo nell’input, un ritardo nell’output o un ritardo I/O durante la costruzione del modello. Il ritardo temporale deve essere un numero intero non negativo che rappresenta un multiplo del tempo di campionamento. Ad esempio,
sys_delay = tf(1, [1 1], 0.01,'ioDelay',5)
restituisce un sistema con un ritardo I/O di 5 s.
Transfer function:
1
z^(-5) * -----
z + 1
Sample time: 0.01
Aggiunta di ritardi ai modelli lineari
È possibile aggiungere ritardi temporali ai modelli a tempo lineare specificando un ritardo nell’input, un ritardo nell’output o un ritardo I/O durante la costruzione del modello. Ad esempio, per aggiungere un ritardo I/O al motore CC, usare questo codice.
sys_tfdelay = tf(1.5,[1 14 40.02],'ioDelay',0.05)
Questo comando costruisce la funzione di trasferimento del motore CC, ma aggiunge un ritardo di 0,05 secondi.
Transfer function:
1.5
exp(-0.05*s) * ------------------
s^2 + 14 s + 40.02
Per ulteriori informazioni sull’aggiunta di ritardi temporali, vedere Time Delays in Linear Systems.
Oggetti LTI
Per comodità, il software Control System Toolbox utilizza strutture di dati personalizzate, denominate oggetti LTI, per salvare i dati relativi al modello. Ad esempio, la variabile sys_dc creata per l'esempio del motore CC è detta oggetto SS. Esistono anche gli oggetti TF, ZPK e FRD, rispettivamente per i modelli a funzione di trasferimento, zero/poli/guadagno e risposta dei dati in frequenza. I quattro oggetti LTI contengono i dati del modello e consentono di manipolare sistemi lineari come entità singole anziché come raccolte di vettori o matrici.
Per visualizzare il contenuto degli oggetti LTI, usare il comando get. Questo codice descrive il contenuto di sys_dc tratto dall’esempio del motore CC.
get(sys_dc)
A: [2×2 double]
B: [2×1 double]
C: [0 1]
D: 0
E: []
Scaled: 0
StateName: {2×1 cell}
StateUnit: {2×1 cell}
InternalDelay: [0×1 double]
InputDelay: 0
OutputDelay: 0
Ts: 0
TimeUnit: 'seconds'
InputName: {''}
InputUnit: {''}
InputGroup: [1×1 struct]
OutputName: {''}
OutputUnit: {''}
OutputGroup: [1×1 struct]
Notes: [0×1 string]
UserData: []
Name: ''
SamplingGrid: [1×1 struct]È possibile manipolare i dati contenuti negli oggetti LTI tramite il comando set; vedere le pagine di riferimento online di Control System Toolbox per la descrizione di set e get.
Un altro modo pratico di impostare o recuperare le proprietà di un modello LTI consiste nell’accedervi direttamente utilizzando la notazione con punto. Ad esempio, se si desidera accedere al valore della matrice A, invece di utilizzare get, si può digitare
sys_dc.A
alla comparsa del prompt MATLAB®. Questa notazione restituisce la matrice A.
ans =
-4.0000 -0.0300
0.7500 -10.0000
Analogamente, se si desidera modificare i valori della matrice A, lo si può fare direttamente, come mostra questo codice.
A_new = [-4.5 -0.05; 0.8 -12.0]; sys_dc.A = A_new;