Deep Learning con ottimizzazione bayesiana
Questo esempio mostra come applicare l'ottimizzazione bayesiana al Deep Learning e trovare gli iperparametri ottimali di rete, nonché le opzioni di addestramento per le reti neurali convoluzionali.
Per addestrare una rete neurale profonda, è necessario specificare l’architettura della rete neurale e le opzioni dell'algoritmo di addestramento. La selezione e il perfezionamento di questi iperparametri può risultare difficile e richiedere del tempo. L'ottimizzazione bayesiana è un algoritmo ben adatto per l’ottimizzazione degli iperparametri dei modelli di classificazione e regressione. È possibile utilizzare l'ottimizzazione bayesiana per ottimizzare funzioni non differenziabili, discontinue e che richiedono molto tempo per essere valutate. L'algoritmo mantiene internamente un modello di processo gaussiano della funzione obiettivo e utilizza le valutazioni della funzione obiettivo per addestrare tale modello.
Questo esempio mostra come:
Scaricare e preparare il set di dati CIFAR-10 per l'addestramento della rete. Questo set di dati è uno dei più utilizzati per testare i modelli di classificazione delle immagini.
Specificare le variabili da ottimizzare utilizzando l'ottimizzazione bayesiana. Queste variabili sono opzioni dell'algoritmo di addestramento e i parametri dell'architettura della rete stessa.
Definire la funzione obiettivo, che considera i valori delle variabili di ottimizzazione come input, specifica l'architettura di rete e le opzioni di addestramento, addestra e convalida la rete e salva la rete addestrata su disco. La funzione obiettivo è definita alla fine di questo script.
Eseguire l'ottimizzazione bayesiana minimizzando l'errore di classificazione sul set di convalida.
Caricare la rete ritenuta ottimale dal disco e valutarla sul set di prova.
In alternativa, l'ottimizzazione bayesiana può essere utilizzata per trovare le opzioni di addestramento ottimali in Experiment Manager. Per ulteriori informazioni, vedere Tune Experiment Hyperparameters by Using Bayesian Optimization.
Preparazione dei dati
Scaricare il set di dati CIFAR-10 [1]. Questo set di dati contiene 60.000 immagini e ogni immagine ha una dimensione di 32x32 e tre canali colore (RGB). L’intero set di dati ha una dimensione di 175 MB. Il processo di download potrebbe richiedere un po' di tempo, in base alla velocità di connessione a Internet.
datadir = tempdir; downloadCIFARData(datadir);
Caricare il set di dati CIFAR-10 come immagini ed etichette di addestramento e come immagini ed etichette di prova. Per consentire la convalida della rete, utilizzare 5000 immagini di prova per la convalida.
[XTrain,YTrain,XTest,YTest] = loadCIFARData(datadir); idx = randperm(numel(YTest),5000); XValidation = XTest(:,:,:,idx); XTest(:,:,:,idx) = []; YValidation = YTest(idx); YTest(idx) = [];
È possibile visualizzare un campione delle immagini di addestramento utilizzando il seguente codice.
figure; idx = randperm(numel(YTrain),20); for i = 1:numel(idx) subplot(4,5,i); imshow(XTrain(:,:,:,idx(i))); end
Scelta delle variabili da ottimizzare
Scegliere le variabili da ottimizzare utilizzando l'ottimizzazione bayesiana e specificare gli intervalli in cui effettuare la ricerca. Specificare inoltre se le variabili sono numeri interi e se effettuare la ricerca nell’intervallo dello spazio logaritmico. Ottimizzare le seguenti variabili:
Profondità della sezione di rete. Questo parametro controlla la profondità della rete. La rete è composta da tre sezioni, ciascuna con livelli convoluzionali identici
SectionDepth. Pertanto, il numero totale di livelli convoluzionali risulta essere3*SectionDepth. La funzione obiettivo successiva nello script considera il numero di filtri convoluzionali in ogni livello proporzionale a1/sqrt(SectionDepth). Di conseguenza, il numero di parametri e la quantità di calcoli richiesti per ciascuna iterazione sono pressoché gli stessi per le diverse profondità di sezione.Velocità di apprendimento inziale. La velocità di apprendimento ottimale può dipendere sia dai dati che dalla rete che si sta addestrando.
Momento stocastico di discesa del gradiente. Il momento aggiunge inerzia agli aggiornamenti dei parametri, facendo in modo che l'aggiornamento corrente contenga un contributo proporzionale all'aggiornamento dell'iterazione precedente. In questo modo si ottengono aggiornamenti dei parametri più uniformi e una riduzione del rumore inerente alla discesa stocastica del gradiente.
Forza di regolarizzazione L2. Utilizzare la regolarizzazione per evitare il sovraadattamento. Cercare nello spazio della forza di regolarizzazione per individuare un valore ottimale. Anche l'aumento dei dati e la normalizzazione dei batch aiutano a regolarizzare la rete.
optimVars = [
optimizableVariable('SectionDepth',[1 3],'Type','integer')
optimizableVariable('InitialLearnRate',[1e-2 1],'Transform','log')
optimizableVariable('Momentum',[0.8 0.98])
optimizableVariable('L2Regularization',[1e-10 1e-2],'Transform','log')];Esecuzione dell'ottimizzazione bayesiana
Creare la funzione obiettivo per l'ottimizzatore bayesiano, utilizzando i dati di addestramento e di convalida come input. La funzione obiettivo addestra una rete neurale convoluzionale e restituisce l'errore di classificazione sul set di convalida. Questa funzione è definita alla fine di questo script. Poiché bayesopt utilizza il tasso di errore sul set di convalida per scegliere il modello migliore, è possibile che la rete finale venga sovradattata nel set di convalida. Il modello finale scelto viene quindi testato sul set di prova indipendente per stimare l'errore di generalizzazione.
ObjFcn = makeObjFcn(XTrain,YTrain,XValidation,YValidation);
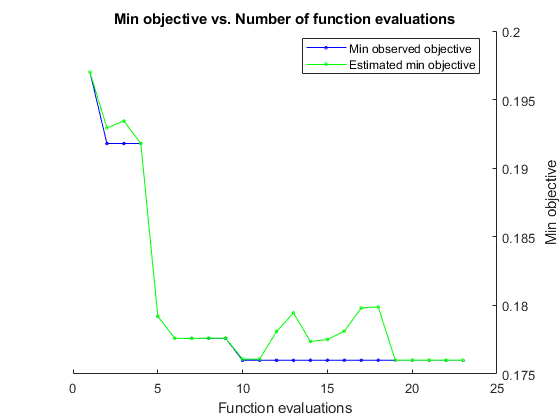
Eseguire l'ottimizzazione bayesiana minimizzando l'errore di classificazione sul set di convalida. Specificare il tempo totale di ottimizzazione in secondi. Per utilizzare al meglio la potenza dell'ottimizzazione bayesiana, è necessario eseguire almeno 30 valutazioni della funzione obiettivo. Per addestrare le reti in parallelo su più GPU, impostare il valore 'UseParallel' su true. Se si dispone di una sola GPU e si imposta il valore 'UseParallel' su true, tutti i worker condivideranno quella GPU con il conseguente risultato che non si otterrà alcuna accelerazione dell'addestramento ma che aumenteranno le probabilità che la GPU esaurisca la memoria.
Al termine dell'addestramento di ciascuna rete, bayesopt stampa i risultati nella finestra di comando. La funzione bayesopt restituisce quindi i nomi dei file in BayesObject.UserDataTrace. La funzione obiettivo salva le reti addestrate su disco e restituisce i nomi dei file a bayesopt.
BayesObject = bayesopt(ObjFcn,optimVars, ... 'MaxTime',14*60*60, ... 'IsObjectiveDeterministic',false, ... 'UseParallel',false);
|===================================================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | SectionDepth | InitialLearn-| Momentum | L2Regulariza-| | | result | | runtime | (observed) | (estim.) | | Rate | | tion | |===================================================================================================================================| | 1 | Best | 0.197 | 955.69 | 0.197 | 0.197 | 3 | 0.61856 | 0.80624 | 0.00035179 |
| 2 | Best | 0.1918 | 790.38 | 0.1918 | 0.19293 | 2 | 0.074118 | 0.91031 | 2.7229e-09 |
| 3 | Accept | 0.2438 | 660.29 | 0.1918 | 0.19344 | 1 | 0.051153 | 0.90911 | 0.00043113 |
| 4 | Accept | 0.208 | 672.81 | 0.1918 | 0.1918 | 1 | 0.70138 | 0.81923 | 3.7783e-08 |
| 5 | Best | 0.1792 | 844.07 | 0.1792 | 0.17921 | 2 | 0.65156 | 0.93783 | 3.3663e-10 |
| 6 | Best | 0.1776 | 851.49 | 0.1776 | 0.17759 | 2 | 0.23619 | 0.91932 | 1.0007e-10 |
| 7 | Accept | 0.2232 | 883.5 | 0.1776 | 0.17759 | 2 | 0.011147 | 0.91526 | 0.0099842 |
| 8 | Accept | 0.2508 | 822.65 | 0.1776 | 0.17762 | 1 | 0.023919 | 0.91048 | 1.0002e-10 |
| 9 | Accept | 0.1974 | 1947.6 | 0.1776 | 0.17761 | 3 | 0.010017 | 0.97683 | 5.4603e-10 |
| 10 | Best | 0.176 | 1938.4 | 0.176 | 0.17608 | 2 | 0.3526 | 0.82381 | 1.4244e-07 |
| 11 | Accept | 0.1914 | 2874.4 | 0.176 | 0.17608 | 3 | 0.079847 | 0.86801 | 9.7335e-07 |
| 12 | Accept | 0.181 | 2578 | 0.176 | 0.17809 | 2 | 0.35141 | 0.80202 | 4.5634e-08 |
| 13 | Accept | 0.1838 | 2410.8 | 0.176 | 0.17946 | 2 | 0.39508 | 0.95968 | 9.3856e-06 |
| 14 | Accept | 0.1786 | 2490.6 | 0.176 | 0.17737 | 2 | 0.44857 | 0.91827 | 1.0939e-10 |
| 15 | Accept | 0.1776 | 2668 | 0.176 | 0.17751 | 2 | 0.95793 | 0.85503 | 1.0222e-05 |
| 16 | Accept | 0.1824 | 3059.8 | 0.176 | 0.17812 | 2 | 0.41142 | 0.86931 | 1.447e-06 |
| 17 | Accept | 0.1894 | 3091.5 | 0.176 | 0.17982 | 2 | 0.97051 | 0.80284 | 1.5836e-10 |
| 18 | Accept | 0.217 | 2794.5 | 0.176 | 0.17989 | 1 | 0.2464 | 0.84428 | 4.4938e-06 |
| 19 | Accept | 0.2358 | 4054.2 | 0.176 | 0.17601 | 3 | 0.22843 | 0.9454 | 0.00098248 |
| 20 | Accept | 0.2216 | 4411.7 | 0.176 | 0.17601 | 3 | 0.010847 | 0.82288 | 2.4756e-08 |
|===================================================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | SectionDepth | InitialLearn-| Momentum | L2Regulariza-| | | result | | runtime | (observed) | (estim.) | | Rate | | tion | |===================================================================================================================================| | 21 | Accept | 0.2038 | 3906.4 | 0.176 | 0.17601 | 2 | 0.09885 | 0.81541 | 0.0021184 |
| 22 | Accept | 0.2492 | 4103.4 | 0.176 | 0.17601 | 2 | 0.52313 | 0.83139 | 0.0016269 |
| 23 | Accept | 0.1814 | 4240.5 | 0.176 | 0.17601 | 2 | 0.29506 | 0.84061 | 6.0203e-10 |
__________________________________________________________
Optimization completed.
MaxTime of 50400 seconds reached.
Total function evaluations: 23
Total elapsed time: 53088.5123 seconds
Total objective function evaluation time: 53050.7026
Best observed feasible point:
SectionDepth InitialLearnRate Momentum L2Regularization
____________ ________________ ________ ________________
2 0.3526 0.82381 1.4244e-07
Observed objective function value = 0.176
Estimated objective function value = 0.17601
Function evaluation time = 1938.4483
Best estimated feasible point (according to models):
SectionDepth InitialLearnRate Momentum L2Regularization
____________ ________________ ________ ________________
2 0.3526 0.82381 1.4244e-07
Estimated objective function value = 0.17601
Estimated function evaluation time = 1898.2641
Valutazione della rete finale
Caricare la rete migliore ottenuta dall'ottimizzazione e dalla relativa precisione di convalida.
bestIdx = BayesObject.IndexOfMinimumTrace(end);
fileName = BayesObject.UserDataTrace{bestIdx};
savedStruct = load(fileName);
valError = savedStruct.valErrorvalError = 0.1760
Prevedere le etichette del set di prova e calcolare l'errore di prova. Trattare la classificazione di ciascuna immagine nel set di prova come evento indipendente con una certa probabilità di successo; quindi, il numero di immagini classificate in modo errato seguirà una distribuzione binomiale. Utilizzare questo elemento per calcolare l'errore standard (testErrorSE) e un intervallo di confidenza approssimativo del 95% (testError95CI) del tasso di errore della generalizzazione. Questo metodo è spesso chiamato metodo Wald. bayesopt determina la rete ottimale utilizzando il set di convalida senza proporre la rete al set di prova. È quindi possibile che l'errore di prova sia superiore all'errore di convalida.
[YPredicted,probs] = classify(savedStruct.trainedNet,XTest); testError = 1 - mean(YPredicted == YTest)
testError = 0.1910
NTest = numel(YTest); testErrorSE = sqrt(testError*(1-testError)/NTest); testError95CI = [testError - 1.96*testErrorSE, testError + 1.96*testErrorSE]
testError95CI = 1×2
0.1801 0.2019
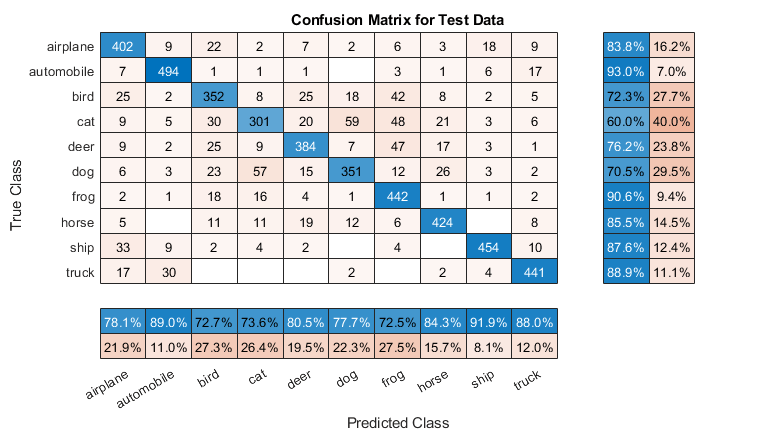
Tracciare la matrice di confusione per i dati del test. Visualizzare la precisione e il richiamo per ciascuna classe utilizzando i riepiloghi di colonna e di riga.
figure('Units','normalized','Position',[0.2 0.2 0.4 0.4]); cm = confusionchart(YTest,YPredicted); cm.Title = 'Confusion Matrix for Test Data'; cm.ColumnSummary = 'column-normalized'; cm.RowSummary = 'row-normalized';
È possibile visualizzare alcune immagini di prova insieme alle classi previste e alle probabilità di tali classi, utilizzando il codice seguente.
figure idx = randperm(numel(YTest),9); for i = 1:numel(idx) subplot(3,3,i) imshow(XTest(:,:,:,idx(i))); prob = num2str(100*max(probs(idx(i),:)),3); predClass = char(YPredicted(idx(i))); label = [predClass,', ',prob,'%']; title(label) end
Funzione obiettivo per l'ottimizzazione
Definire la funzione obiettivo per l'ottimizzazione. Questa funzione esegue i seguenti passaggi:
Considera i valori delle variabili di ottimizzazione come input.
bayesoptrichiama la funzione obiettivo con i valori correnti delle variabili di ottimizzazione in una tabella con il nome di ogni colonna uguale al nome della variabile. Ad esempio, il valore attuale della profondità della sezione di rete èoptVars.SectionDepth.Definisce l'architettura di rete e le opzioni di addestramento.
Addestra e convalida la rete.
Salva su disco la rete addestrata, l'errore di convalida e le opzioni di addestramento.
Restituisce l'errore di convalida e il nome del file della rete salvata.
function ObjFcn = makeObjFcn(XTrain,YTrain,XValidation,YValidation) ObjFcn = @valErrorFun; function [valError,cons,fileName] = valErrorFun(optVars)
Definire l’architettura della rete neurale convoluzionale.
Aggiungere un riempimento ai livelli convoluzionali in modo che la dimensione dell'output spaziale sia sempre uguale a quella dell'input.
Ogni volta che si riduce il campionamento delle dimensioni spaziali di un fattore di due utilizzando i livelli di raggruppamento massimi, si aumenta il numero di filtri di un fattore di due. In questo modo si garantisce che la quantità di calcolo richiesta in ciascun livello convoluzionale sia pressoché la stessa.
Scegliere il numero di filtri proporzionale a
1/sqrt(SectionDepth), in modo che reti con profondità diversa abbiano all'incirca lo stesso numero di parametri e richiedano circa la stessa quantità di calcolo per iterazione. Per aumentare il numero di parametri di rete e la flessibilità complessiva della rete, incrementarenumF. Per addestrare reti ancora più profonde, modificare l'intervallo della variabileSectionDepth.Utilizzare
convBlock(filterSize,numFilters,numConvLayers)per creare un blocco di livelli convoluzionalinumConvLayers, ciascuno con filtrifilterSizeenumFiltersspecificati e ciascuno seguito da un livello di normalizzazione batch e da un livello ReLU. La funzioneconvBlockè specificata alla fine di questo esempio.
imageSize = [32 32 3];
numClasses = numel(unique(YTrain));
numF = round(16/sqrt(optVars.SectionDepth));
layers = [
imageInputLayer(imageSize)
% The spatial input and output sizes of these convolutional
% layers are 32-by-32, and the following max pooling layer
% reduces this to 16-by-16.
convBlock(3,numF,optVars.SectionDepth)
maxPooling2dLayer(3,'Stride',2,'Padding','same')
% The spatial input and output sizes of these convolutional
% layers are 16-by-16, and the following max pooling layer
% reduces this to 8-by-8.
convBlock(3,2*numF,optVars.SectionDepth)
maxPooling2dLayer(3,'Stride',2,'Padding','same')
% The spatial input and output sizes of these convolutional
% layers are 8-by-8. The global average pooling layer averages
% over the 8-by-8 inputs, giving an output of size
% 1-by-1-by-4*initialNumFilters. With a global average
% pooling layer, the final classification output is only
% sensitive to the total amount of each feature present in the
% input image, but insensitive to the spatial positions of the
% features.
convBlock(3,4*numF,optVars.SectionDepth)
averagePooling2dLayer(8)
% Add the fully connected layer and the final softmax and
% classification layers.
fullyConnectedLayer(numClasses)
softmaxLayer
classificationLayer];Specificare le opzioni per l'addestramento della rete. Ottimizzare la velocità di apprendimento iniziale, il momento SGD e la forza di regolarizzazione L2.
Specificare i dati di convalida e scegliere il valore 'ValidationFrequency' in modo che trainNetwork convalidi la rete una volta per epoca. Eseguire l’addestramento per un numero fisso di epoche, quindi ridurre la velocità di apprendimento di un fattore 10 durante le ultime epoche. In questo modo si riduce il rumore legato agli aggiornamenti dei parametri e i parametri di rete si stabilizzano più vicino a un minimo della funzione di perdita.
miniBatchSize = 256;
validationFrequency = floor(numel(YTrain)/miniBatchSize);
options = trainingOptions('sgdm', ...
'InitialLearnRate',optVars.InitialLearnRate, ...
'Momentum',optVars.Momentum, ...
'MaxEpochs',60, ...
'LearnRateSchedule','piecewise', ...
'LearnRateDropPeriod',40, ...
'LearnRateDropFactor',0.1, ...
'MiniBatchSize',miniBatchSize, ...
'L2Regularization',optVars.L2Regularization, ...
'Shuffle','every-epoch', ...
'Verbose',false, ...
'Plots','training-progress', ...
'ValidationData',{XValidation,YValidation}, ...
'ValidationFrequency',validationFrequency);Utilizzare l'incremento dei dati per capovolgere casualmente le immagini di addestramento lungo l'asse verticale e traslare casualmente fino a quattro pixel in orizzontale e in verticale. L’aumento dei dati aiuta la rete ad evitare l’overfitting e a memorizzare i dettagli esatti delle immagini di addestramento.
pixelRange = [-4 4];
imageAugmenter = imageDataAugmenter( ...
'RandXReflection',true, ...
'RandXTranslation',pixelRange, ...
'RandYTranslation',pixelRange);
datasource = augmentedImageDatastore(imageSize,XTrain,YTrain,'DataAugmentation',imageAugmenter);Addestrare la rete e tracciare i progressi dell'addestramento durante l’addestramento. Chiudere tutti i grafici di addestramento al termine dello stesso.
trainedNet = trainNetwork(datasource,layers,options);
close(findall(groot,'Tag','NNET_CNN_TRAININGPLOT_UIFIGURE'))
Valutare la rete addestrata sul set di convalida, calcolare le etichette delle immagini previste e il tasso di errore sui dati di convalida.
YPredicted = classify(trainedNet,XValidation);
valError = 1 - mean(YPredicted == YValidation);Creare un nome del file che contenga l'errore di convalida e salvare su disco la rete, l'errore di convalida e le opzioni di addestramento. La funzione obiettivo restituisce fileName come argomento di output e bayesopt restituisce tutti i nomi dei file in BayesObject.UserDataTrace. L'argomento di output supplementare richiesto cons specifica i vincoli tra le variabili. Non esistono vincoli variabili.
fileName = num2str(valError) + ".mat"; save(fileName,'trainedNet','valError','options') cons = []; end end
La funzione convBlock crea un blocco di livelli convoluzionali numConvLayers, ciascuno con filtri filterSize e numFilters specificati e ciascuno seguito da un livello di normalizzazione batch e da un livello ReLU.
function layers = convBlock(filterSize,numFilters,numConvLayers) layers = [ convolution2dLayer(filterSize,numFilters,'Padding','same') batchNormalizationLayer reluLayer]; layers = repmat(layers,numConvLayers,1); end
Riferimenti
[1] Krizhevsky, Alex. "Learning multiple layers of features from tiny images." (2009). https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf
Vedi anche
Experiment Manager | trainnet | trainingOptions | dlnetwork | bayesopt (Statistics and Machine Learning Toolbox)