LU Factorization

R2026b

Factor square matrix into lower and upper triangular components

• 

LU Factorization block

To add a block to a model, double-click the canvas and start typing the block name. Then, select the block from the list.

Libraries:
DSP System Toolbox / Math Functions / Matrices and Linear Algebra / Matrix Factorizations

Description

The LU Factorization block factors a row-permuted version of the square input matrix A as A_p = L*U, where L is a unit-lower triangular matrix, U is an upper triangular matrix, and A_p contains the rows of A permuted as indicated by the permutation index vector P. The block uses the pivot matrix A_p instead of the exact input matrix A because it improves the numerical accuracy of the factorization.

Examples

Factorize Matrix Using LU Factorization Block

Factorize a matrix using the LU Factorization block.

• Open Model

Ports

Input

A — Input matrix

M-by-M square matrix

Specify the input matrix as an M-by-M square matrix through this port. If the input matrix is fixed point, it must be signed integer or signed fixed point with power-of-two slope and zero bias.

Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes

Output

LU — Lower and upper triangular factors

M-by-M square matrix

Composite matrix containing both the lower triangle elements of L and the upper triangle elements of U. The composite matrix improves the efficiency of the block. The matrix output is in a different format than the output of the lu function, which returns L and U as separate matrices. To convert the output from the LU port of the block to separate L and U matrices, use the following code:

L = tril(LU,-1)+eye(size(LU)); U = triu(LU); 

If you compare the results produced by these equations to the actual output of the lu function, you might see slightly different values. These differences are due to a rounding error, and are expected. For more information on the LU factorizations, see the lu function page.

This composite matrix has the same size, data type, and complexity as the input matrix A.

Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes

P — Permutation vector

vector

Permutation vector, returned as a vector of length M. The block permutes the input square matrix A using the permutation vector P and factors the permuted matrix into unit-lower triangular L and upper triangular matrix U.

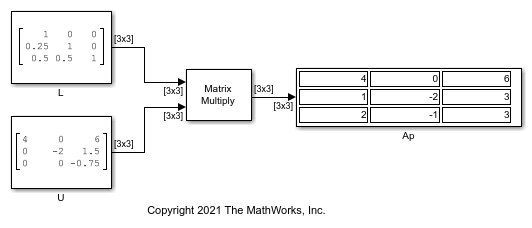
Consider the following input matrix.

$$A=\left[\begin{array}{ccc}1& -2& 3\\ 4& 0& 6\\ 2& -1& 3\end{array}\right]$$

With a permutation index vector P that is equal to $$P=\left[\begin{array}{c}2\\ 1\\ 3\end{array}\right]$$, the permuted matrix A_p becomes:

$$A_p=\left[\begin{array}{ccc}4& 0& 6\\ 1& -2& 3\\ 2& -1& 3\end{array}\right]$$

The block factors this matrix into upper and lower triangular matrices. For a more detailed version of this example, see Factorize Matrix Using LU Factorization Block.

Data Types: single | double | uint32

S — Singularity of input matrix

logical scalar

You can determine the singularity of the input matrix A by enabling the optional output port S. When A is singular, the block outputs a 1 at port S. When A is nonsingular, the block outputs a 0.

Data Types: Boolean

Parameters

Main Tab

Show singularity status — Show singularity status

off (default) | on

Select to output the singularity of the input at port S, which outputs Boolean data type values of 1 or 0. An output of 1 indicates that the current input is singular, and an output of 0 indicates the current input is nonsingular.

Data Types Tab

Rounding mode — Method of rounding operation

Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero

Specify the rounding mode for fixed-point operations as one of the following:

• Floor

• Ceiling

• Convergent

• Nearest

• Round

• Simplest

• Zero

For more details, see rounding mode.

Saturate on integer overflow — Method of overflow action

off (default) | on

When you select this parameter, the block saturates the result of its fixed-point operation. When you clear this parameter, the block wraps the result of its fixed-point operation. For details on saturate and wrap, see overflow mode for fixed-point operations.

Product output — Product output data type

Inherit: Inherit via internal rule (default) | Inherit: Same as input | fixdt(1,16,0)

Product output specifies the data type of the output of a product operation in the LU Factorization block. For more information on the product output data type, see Fixed-Point Data Types and Multiplication Data Types.

• Inherit: Inherit via internal rule — The block inherits the product output data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.

• Inherit: Same as input — The block specifies the product output data type to be the same as the input data type.

• fixdt(1,16,0) — The block specifies a signed, binary-point, scaled, fixed-point data type with a word length of 16 bits and a fraction length of 0.

Alternatively, you can set the Product output data type by using the Data Type Assistant. To use the assistant, click the Show data type assistant button .

For more information on the data type assistant, see Specify Data Types Using Data Type Assistant (Simulink).

Accumulator — Accumulator data type

Inherit: Inherit via internal rule (default) | Inherit: Same as input | Inherit: Same as product output | fixdt(1,16,0)

Accumulator specifies the data type of the output of an accumulation operation in the LU Factorization block. For more information on how to use the accumulator data type in this block, see the Fixed-Point Data Types section.

• Inherit: Inherit via internal rule — The block inherits the accumulator data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.

• Inherit: Same as input — The block specifies the accumulator data type to be the same as the input data type.

• Inherit: Same as product output — The block specifies the accumulator data type to be the same as the product output data type.

• fixdt(1,16,0) — The block specifies a signed, binary-point scaled, fixed-point data type with a word length of 16 bits and a fraction length of 0.

Alternatively, you can set the Accumulator data type by using the Data Type Assistant. To use the assistant, click the Show data type assistant button .

For more information on the data type assistant, see Specify Data Types Using Data Type Assistant (Simulink).

Output — Output data type

Inherit: Same as input (default) | fixdt(1,16,0)

Output specifies the data type of the output of the LU Factorization block. For more information on the output data type, see the Fixed-Point Data Types section.

• Inherit: Same as input — The block specifies the output data type to be the same as the input data type.

• fixdt(1,16,0) — The block specifies a signed, binary-point scaled, fixed-point data type with a word length of 16 bits and a fraction length of 0.

Alternatively, you can set the Output data type by using the Data Type Assistant. To use the assistant, click the Show data type assistant button.

For more information on the data type assistant, see Specify Data Types Using Data Type Assistant (Simulink).

Output Minimum — Minimum value the block can output

[] (default) | scalar

Specify the minimum value the block can output. Simulink^® software uses this minimum value to perform:

• Simulation range checking. See Specify Signal Ranges (Simulink).

• Automatic scaling of fixed-point data types.

Output Maximum — Maximum value block can output

[] (default) | scalar

Specify the maximum value the block can output. Simulink software uses this maximum value to perform:

• Simulation range checking. See Specify Signal Ranges (Simulink).

• Automatic scaling of fixed-point data types.

Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types

off (default) | on

Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.

Block Characteristics

Data Types	double | fixed point | integer | single
Direct Feedthrough	no
Multidimensional Signals	no
Variable-Size Signals	no
Zero-Crossing Detection	no

Programmatic Use: Add Block

To add the block programmatically, use the add_block function with one of these library block paths as the source.

"dspfactors/LU Factorization"

Example: add_block("dspfactors/LU Factorization","myModel/myBlock",MakeNameUnique="on")

More About

Fixed-Point Data Types

The following diagram shows the data types used within the LU Factorization block for fixed-point signals.

You can set the product output, accumulator, and output data types in the block dialog as discussed below.

The output of the multiplier is in the product output data type when the input is real. When the input is complex, the result of the multiplication is in the accumulator data type. For details on the complex multiplication performed, see Multiplication Data Types.

References

[1] Golub, G. H., and C. F. Van Loan. Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

Generated code relies on the memcpy or memset function (string.h) under certain conditions.

Version History

Introduced before R2006a