Minimizzazione vincolata utilizzando ga, basata sui problemi
Questo esempio mostra come minimizzare una funzione obiettivo, soggetta a vincoli e limiti di disuguaglianza non lineare, utilizzando ga nell'approccio basato sui problemi. Per una versione di questo problema basata sul risolutore, vedere Minimizzazione vincolata utilizzando l'algoritmo genetico .
Problema di minimizzazione vincolata
Per questo problema, la funzione di idoneità da minimizzare è una semplice funzione delle variabili 2-D X e Y.
camxy = @(X,Y)(4 - 2.1.*X.^2 + X.^4./3).*X.^2 + X.*Y + (-4 + 4.*Y.^2).*Y.^2;
Questa funzione è descritta in Dixon e Szego [1].
Inoltre, il problema presenta vincoli e limiti non lineari.
x*y + x - y + 1.5 <= 0 (nonlinear constraint) 10 - x*y <= 0 (nonlinear constraint) 0 <= x <= 1 (bound) 0 <= y <= 13 (bound)
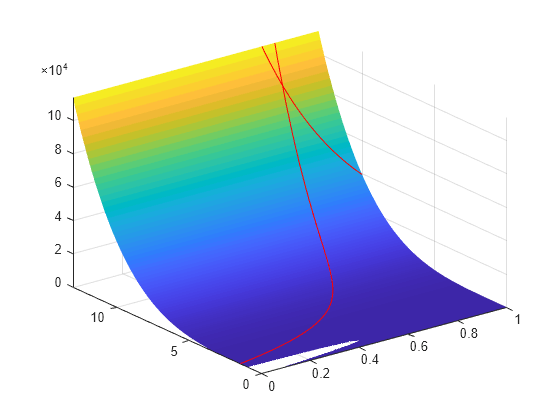
Rappresentare graficamente la regione del vincolo non lineare su un grafico di superficie della funzione di idoneità. I vincoli limitano la soluzione alla piccola regione sopra entrambe le curve rosse.
x1 = linspace(0,1); y1 = (-x1 - 1.5)./(x1 - 1); y2 = 10./x1; [X,Y] = meshgrid(x1,linspace(0,13)); Z = camxy(X,Y); surf(X,Y,Z,"LineStyle","none") hold on z1 = camxy(x1,y1); z2 = camxy(x1,y2); plot3(x1,y1,z1,'r-',x1,y2,z2,'r-') xlim([0 1]) ylim([0 13]) zlim([0,max(Z,[],"all")]) hold off
Creare variabili di ottimizzazione, problemi e vincoli
Per impostare questo problema, creare le variabili di ottimizzazione x e y. Imposta i limiti quando crei le variabili.
x = optimvar("x","LowerBound",0,"UpperBound",1); y = optimvar("y","LowerBound",0,"UpperBound",13);
Creare l'obiettivo come espressione di ottimizzazione.
cam = camxy(x,y);
Creare un problema di ottimizzazione con questa funzione obiettivo.
prob = optimproblem("Objective",cam);Creare i due vincoli di disuguaglianza non lineare e includerli nel problema.
prob.Constraints.cons1 = x*y + x - y + 1.5 <= 0; prob.Constraints.cons2 = 10 - x*y <= 0;
Rivedi il problema.
show(prob)
OptimizationProblem :
Solve for:
x, y
minimize :
(((((4 - (2.1 .* x.^2)) + (x.^4 ./ 3)) .* x.^2) + (x .* y)) + (((-4) + (4 .* y.^2)) .* y.^2))
subject to cons1:
((((x .* y) + x) - y) + 1.5) <= 0
subject to cons2:
(10 - (x .* y)) <= 0
variable bounds:
0 <= x <= 1
0 <= y <= 13
Risolvi problema
Risolvi il problema specificando il risolutore ga.
[sol,fval] = solve(prob,"Solver","ga")
Solving problem using ga. Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
sol = struct with fields:
x: 0.8122
y: 12.3103
fval = 9.1268e+04
Aggiungi visualizzazione
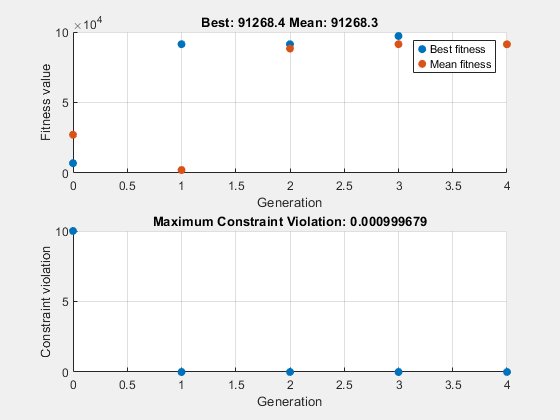
Per osservare i progressi del risolutore, specificare le opzioni che selezionano due funzioni di grafico. La funzione di grafico gaplotbestf traccia il miglior valore della funzione obiettivo a ogni iterazione, mentre la funzione di grafico gaplotmaxconstr traccia la massima violazione del vincolo a ogni iterazione. Imposta queste due funzioni di grafico in una matrice di celle. Inoltre, è possibile visualizzare informazioni sullo stato di avanzamento del risolutore nella finestra di comando impostando l'opzione Display su 'iter'.
options = optimoptions(@ga,... 'PlotFcn',{@gaplotbestf,@gaplotmaxconstr},... 'Display','iter');
Eseguire il risolutore, incluso l'argomento options.
[sol,fval] = solve(prob,"Solver","ga","Options",options)
Solving problem using ga.
Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2520 91357.8 0 0
2 4982 91324.1 4.55e-05 0 3 7914 97166.6 0 0
4 16145 91268.4 0.0009997 0Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
sol = struct with fields:
x: 0.8123
y: 12.3103
fval = 9.1268e+04
I vincoli non lineari fanno sì che ga risolva molti sottoproblemi a ogni iterazione. Come mostrato sia nei grafici che nella visualizzazione iterativa, il processo di soluzione prevede poche iterazioni. Tuttavia, la colonna Func-count nella visualizzazione iterativa mostra molte valutazioni di funzioni per iterazione.
Funzioni non supportate
Se le funzioni di vincolo obiettivo o non lineare non sono supportate (vedere Supported Operations for Optimization Variables and Expressions), utilizzare fcn2optimexpr per convertirle in una forma adatta all'approccio basato sui problemi. Ad esempio, supponiamo che al posto del vincolo , si abbia il vincolo , dove è la funzione di Bessel modificata besseli(1,x). (Le funzioni di Bessel non sono funzioni supportate.) Crea questo vincolo usando fcn2optimexpr . Per prima cosa, crea un'espressione di ottimizzazione per .
bfun = fcn2optimexpr(@(t,u)besseli(1,t) + besseli(1,u),x,y);
Quindi, sostituisci il vincolo cons2 con il vincolo bfun >= 10 .
prob.Constraints.cons2 = bfun >= 10;
Risolvere il problema. La soluzione è diversa perché la regione di vincolo è diversa.
[sol2,fval2] = solve(prob,"Solver","ga","Options",options)
Solving problem using ga.
Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2512 974.044 0 0
2 4974 960.998 0 0 3 7436 963.12 0 0
4 12001 960.83 0.0009335 0Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

sol2 = struct with fields:
x: 0.4999
y: 3.9979
fval2 = 960.8300
Riferimenti
[1] Dixon, L. C. W., e G .P. Szego (a cura di). Verso l'ottimizzazione globale 2. Olanda Settentrionale: Elsevier Science Ltd., Amsterdam, 1978.
Vedi anche
ga | solve | fcn2optimexpr