Questa pagina è stata tradotta con la traduzione automatica. Fai clic qui per vedere l'ultima versione in inglese.

ga

Trova il minimo della funzione usando l'algoritmo genetico

Sintassi

x = ga(fun,nvars)

x = ga(fun,nvars,A,b)

x = ga(fun,nvars,A,b,Aeq,beq)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

x = ga(problem)

[x,fval] = ga(___)

[x,fval,exitflag,output] = ga(___)

[x,fval,exitflag,output,population,scores] = ga(___)

Descrizione

x = ga(fun,nvars) trova un minimo locale non vincolato, x, per la funzione obiettivo, fun . nvars è la dimensione (numero di variabili di progettazione) di fun .

Nota

Passing Extra Parameters spiega come passare parametri aggiuntivi alla funzione obiettivo e alle funzioni di vincolo non lineare, se necessario.

x = ga(fun,nvars,A,b) trova un minimo locale x a fun, soggetto alle disuguaglianze lineari A*x ≤ b . ga valuta il prodotto di matrice A*x come se x fosse trasposto (A*x').

x = ga(fun,nvars,A,b,Aeq,beq) trova un minimo locale x a fun, soggetto alle uguaglianze lineari Aeq*x = beq e A*x ≤ b . (Impostare A=[] e b=[] se non esistono disuguaglianze lineari.) ga valuta il prodotto di matrice Aeq*x come se x fosse trasposto (Aeq*x').

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub) definisce un insieme di limiti inferiori e superiori sulle variabili di progettazione, x, in modo che una soluzione venga trovata nell'intervallo lb ≤ x ≤ ub . (Impostare Aeq=[] e beq=[] se non esistono uguaglianze lineari.)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon) sottopone la minimizzazione ai vincoli definiti in nonlcon . La funzione nonlcon accetta x e restituisce i vettori C e Ceq, che rappresentano rispettivamente le disuguaglianze e le uguaglianze non lineari. ga minimizza fun in modo che C(x) ≤ 0 e Ceq(x) = 0 . (Impostare lb=[] e ub=[] se non esistono limiti.)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options) si riduce al minimo con i parametri di ottimizzazione predefiniti sostituiti dai valori in options. (Impostare nonlcon=[] se non esistono vincoli non lineari.) Crea options utilizzando optimoptions .

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon) o x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options) richiedono che le variabili elencate in intcon assumano valori interi.

Nota

In presenza di vincoli interi, ga non accetta vincoli di uguaglianza non lineare, ma solo vincoli di disuguaglianza non lineare.

x = ga(problem) trova il minimo per problem, una struttura descritta in problem .

[x,fval] = ga(___), per tutti gli argomenti di input precedenti, restituisce anche fval, il valore della funzione di fitness in x .

[x,fval,exitflag,output] = ga(___) restituisce anche exitflag, un numero intero che identifica il motivo per cui l'algoritmo è terminato, e output, una struttura che contiene l'output di ciascuna generazione e altre informazioni sulle prestazioni dell'algoritmo.

[x,fval,exitflag,output,population,scores] = ga(___) restituisce anche una matrice population, le cui righe sono la popolazione finale, e un vettore scores, i punteggi della popolazione finale.

Esempi

Ottimizzare una funzione non regolare utilizzando ga

Quando si esegue questo esempio, viene incluso il file ps_example.m. Rappresenta graficamente la funzione.

xi = linspace(-6,2,300);
yi = linspace(-4,4,300);
[X,Y] = meshgrid(xi,yi);
Z = ps_example([X(:),Y(:)]);
Z = reshape(Z,size(X));
surf(X,Y,Z,'MeshStyle','none')
colormap 'jet'
view(-26,43)
xlabel('x(1)')
ylabel('x(2)')
title('ps\_example(x)')

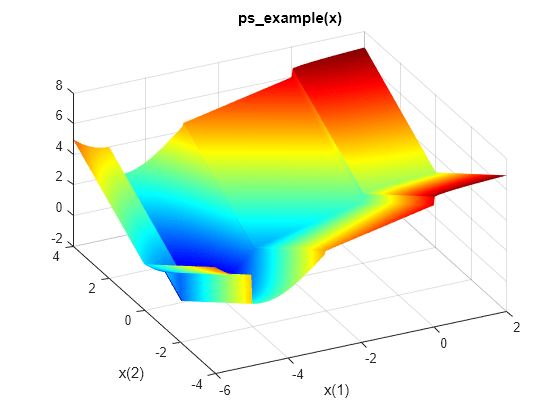
Trova il minimo di questa funzione usando ga .

rng default % For reproducibility
x = ga(@ps_example,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6793   -0.0860

Minimizzare una funzione non regolare con vincoli lineari

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example sulla regione x(1) + x(2) >= 1 e x(2) <= 5 + x(1). Questa funzione è inclusa quando si esegue questo esempio.

Per prima cosa, convertiamo i due vincoli di disuguaglianza nella forma matriciale A*x <= b . In altre parole, prendi le variabili x sul lato sinistro della disuguaglianza e rendi entrambe le disuguaglianze minori o uguali:

-x(1) -x(2) <= -1

-x(1) + x(2) <= 5

A = [-1,-1;
    -1,1];
b = [-1;5];

Risolvi il problema vincolato usando ga .

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    0.9990    0.0000

I vincoli sono soddisfatti entro il valore predefinito della tolleranza del vincolo, 1e-3. Per vederlo, calcola A*x' - b, che dovrebbe avere componenti negative.

disp(A*x' - b)

    0.0010
   -5.9990

Minimizzare una funzione non regolare con vincoli di uguaglianza e disuguaglianza lineare

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example sulla regione x(1) + x(2) >= 1 e x(2) == 5 + x(1). Questa funzione è inclusa quando si esegue questo esempio.

Per prima cosa, convertiamo i due vincoli nella forma matriciale A*x <= b e Aeq*x = beq. In altre parole, prendi le variabili x sul lato sinistro delle espressioni e trasforma la disuguaglianza nella forma minore o uguale:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Risolvi il problema vincolato usando ga .

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -2.0005    2.9995

Verificare che i vincoli siano soddisfatti entro il valore predefinito di ConstraintTolerance, 1e-3.

disp(A*x' - b)

   1.0000e-03

disp(Aeq*x' - beq)

   8.5897e-09

Ottimizzazione con vincoli e limiti lineari

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example sulla regione x(1) + x(2) >= 1 e x(2) == 5 + x(1). Quando si esegue questo esempio, viene inclusa la funzione ps_example. Inoltre, impostare i limiti 1 <= x(1) <= 6 e -3 <= x(2) <= 8.

Per prima cosa, convertiamo i due vincoli lineari nella forma matriciale A*x <= b e Aeq*x = beq. In altre parole, prendi le variabili x sul lato sinistro delle espressioni e trasforma la disuguaglianza nella forma minore o uguale:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Imposta i limiti lb e ub .

lb = [1 -3];
ub = [6 8];

Risolvi il problema vincolato usando ga .

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,lb,ub)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    1.0000    6.0000

Verificare che i vincoli lineari siano soddisfatti entro il valore predefinito di ConstraintTolerance, 1e-3.

disp(A*x' - b)

   -6.0000

disp(Aeq*x' - beq)

  -7.9765e-08

Ottimizzazione con vincoli non lineari utilizzando ga

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example sulla regione $2{\mathit{x}}_1^2+{\mathit{x}}_2^2\le 3$ e $$(x_1+1{)}^2=(x_2/2{)}^4$$. Quando si esegue questo esempio, viene inclusa la funzione ps_example.

Per farlo, utilizzare la funzione ellipsecons.m che restituisce il vincolo di disuguaglianza nel primo output, c, e il vincolo di uguaglianza nel secondo output, ceq. Quando si esegue questo esempio, viene inclusa la funzione ellipsecons. Esaminare il codice ellipsecons.

type ellipsecons

function [c,ceq] = ellipsecons(x)

c = 2*x(1)^2 + x(2)^2 - 3;
ceq = (x(1)+1)^2 - (x(2)/2)^4;

Includere una funzione handle per ellipsecons come argomento nonlcon.

nonlcon = @ellipsecons;
fun = @ps_example;
rng default % For reproducibility
x = ga(fun,2,[],[],[],[],[],[],nonlcon)

Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -0.9766    0.0362

Verificare che i vincoli non lineari siano soddisfatti in x . I vincoli sono soddisfatti quando c ≤ 0 e ceq = 0 entro il valore predefinito di ConstraintTolerance, 1e-3 .

[c,ceq] = nonlcon(x)

c = -1.0911

ceq = 5.4645e-04

Riduci a icona con opzioni non predefinite

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example sulle regioni x(1) + x(2) >= 1 e x(2) == 5 + x(1) utilizzando una tolleranza di vincolo inferiore a quella predefinita. Quando si esegue questo esempio, viene inclusa la funzione ps_example.

Per prima cosa, convertiamo i due vincoli nella forma matriciale A*x <= b e Aeq*x = beq. In altre parole, prendi le variabili x sul lato sinistro delle espressioni e trasforma la disuguaglianza nella forma minore o uguale:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Per ottenere una soluzione più accurata, impostare una tolleranza di vincolo pari a 1e-6. Per monitorare i progressi del risolutore, imposta una funzione di grafico.

options = optimoptions('ga','ConstraintTolerance',1e-6,'PlotFcn', @gaplotbestf);

Risolvere il problema di minimizzazione.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,[],[],[],options)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -2.0000    3.0000

Verificare che i vincoli lineari siano soddisfatti entro 1e-6 .

disp(A*x' - b)

   9.9809e-07

disp(Aeq*x' - beq)

  -7.3589e-08

Minimizzare una funzione non lineare con vincoli interi

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example soggetta al vincolo che x(1) sia un numero intero. Questa funzione è inclusa quando si esegue questo esempio.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

Ottenere la soluzione e il valore della funzione

Utilizzare l'algoritmo genetico per minimizzare un problema non lineare vincolato a numeri interi. Ottenere sia la posizione del minimo che il valore minimo della funzione. Quando si esegue questo esempio, viene inclusa la funzione obiettivo ps_example.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = -1.8344

Confronta questo risultato con la soluzione del problema senza vincoli.

[x,fval] = ga(fun,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6906   -0.0078

fval = -1.9918

Ottenere informazioni diagnostiche

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example vincolata ad avere valori interi x(1). Quando si esegue questo esempio, viene inclusa la funzione ps_example. Per comprendere il motivo per cui il risolutore si è fermato e come ga ha cercato un minimo, ottenere i risultati exitflag e output. Inoltre, tracciare il grafico del valore minimo osservato della funzione obiettivo man mano che il risolutore procede.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
options = optimoptions('ga','PlotFcn', @gaplotbestf);
[x,fval,exitflag,output] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = -1.8344

exitflag = 1

output = struct with fields:
      problemtype: 'integerconstraints'
         rngstate: [1x1 struct]
      generations: 86
        funccount: 3311
          message: 'ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and ...'
    maxconstraint: 0
       hybridflag: []

Ottieni la popolazione finale e i punteggi

Utilizzare l'algoritmo genetico per minimizzare la funzione ps_example vincolata ad avere valori interi x(1). Quando si esegue questo esempio, viene inclusa la funzione ps_example. Ottenere tutti gli output, inclusa la popolazione finale e il vettore dei punteggi.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval,exitflag,output,population,scores] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon);

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

Esaminare i primi 10 membri della popolazione finale e i punteggi corrispondenti. Si noti che x(1) ha valore intero per tutti i membri della popolazione. L'algoritmo intero ga genera solo popolazioni fattibili a livello intero.

disp(population(1:10,:))

   1.0e+03 *

   -0.0050   -0.0001
   -0.0050   -0.0001
   -1.6420    0.0027
   -1.5070    0.0010
   -0.4540    0.0104
   -0.2530   -0.0011
   -0.1210   -0.0003
   -0.1040    0.1314
   -0.0140   -0.0010
    0.0160   -0.0002

disp(scores(1:10))

   1.0e+06 *

   -0.0000
   -0.0000
    2.6798
    2.2560
    0.2016
    0.0615
    0.0135
    0.0099
    0.0001
    0.0000

Argomenti di input

fun — Funzione obiettivo

funzione handle | nome della funzione

Funzione obiettivo, specificata come funzione handle o nome di funzione. Scrivere la funzione obiettivo in modo che accetti un vettore riga di lunghezza nvars e restituisca un valore scalare.

Quando l'opzione 'UseVectorized' è true, scrivere fun per accettare una matrice pop per nvars, dove pop è la dimensione attuale della popolazione. In questo caso, fun restituisce un vettore della stessa lunghezza di pop contenente i valori della funzione di fitness. Assicurarsi che fun non assuma alcuna dimensione particolare per pop, poiché ga può superare un singolo membro di una popolazione anche in un calcolo vettorializzato.

Esempio fun = @(x)(x-[4,2]).^2

Tipi di dati: char | function_handle | string

nvars — Numero di variabili

intero positivo

Numero di variabili, specificato come numero intero positivo. Il risolutore passa i vettori riga di lunghezza nvars a fun.

Esempio 4

Tipi di dati: double

A — Vincoli di disuguaglianza lineare

matrice reale

Vincoli di disuguaglianza lineare, specificati come matrice reale. A è una matrice M per nvars, dove M è il numero di disuguaglianze.

A codifica le disuguaglianze lineari M

A*x <= b,

dove x è il vettore colonna delle variabili nvars x(:) e b è un vettore colonna con elementi M.

Ad esempio, per specificare

x₁ + 2 x₂ ≤ 10
3 x₁ + 4 x₂ ≤ 20
5 x₁ + 6 x₂ ≤ 30,

dare questi vincoli:

A = [1,2;3,4;5,6];
b = [10;20;30];

Esempio Per specificare che la somma delle variabili di controllo sia pari o inferiore a 1, specificare i vincoli A = ones(1,N) e b = 1.

Tipi di dati: double

b — Vincoli di disuguaglianza lineare

vettore reale

Vincoli di disuguaglianza lineare, specificati come vettore reale. b è un vettore di elementi M correlato alla matrice A. Se si passa b come vettore riga, i risolutori convertono internamente b nel vettore colonna b(:).

b codifica le disuguaglianze lineari M

A*x <= b,

dove x è il vettore colonna delle variabili N x(:) e A è una matrice di dimensione M per N .

Ad esempio, per specificare

x₁ + 2 x₂ ≤ 10
3 x₁ + 4 x₂ ≤ 20
5 x₁ + 6 x₂ ≤ 30,

dare questi vincoli:

A = [1,2;3,4;5,6];
b = [10;20;30];

Esempio Per specificare che la somma delle variabili di controllo sia pari o inferiore a 1, specificare i vincoli A = ones(1,N) e b = 1.

Tipi di dati: double

Aeq — Vincoli di uguaglianza lineare

matrice reale

Vincoli di uguaglianza lineare, specificati come matrice reale. Aeq è una matrice Me per nvars, dove Me è il numero di uguaglianze.

Aeq codifica le uguaglianze lineari Me

Aeq*x = beq,

dove x è il vettore colonna delle variabili N x(:) e beq è un vettore colonna con elementi Me.

Ad esempio, per specificare

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

dare questi vincoli:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Esempio Per specificare che la somma delle variabili di controllo sia 1, specificare i vincoli Aeq = ones(1,N) e beq = 1.

Tipi di dati: double

beq — Vincoli di uguaglianza lineare

vettore reale

Vincoli di uguaglianza lineare, specificati come vettore reale. beq è un vettore di elementi Me correlato alla matrice Aeq. Se si passa beq come vettore riga, i risolutori convertono internamente beq nel vettore colonna beq(:).

beq codifica le uguaglianze lineari Me

Aeq*x = beq,

dove x è il vettore colonna delle variabili N x(:) e Aeq è una matrice di dimensione Meq per N .

Ad esempio, per specificare

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

dare questi vincoli:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Esempio Per specificare che la somma delle variabili di controllo sia 1, specificare i vincoli Aeq = ones(1,N) e beq = 1.

Tipi di dati: double

lb — Limiti inferiori

[] (predefinito) | array o array reale

Limiti inferiori, specificati come array reale o array di double. lb rappresenta i limiti inferiori elemento per elemento in lb ≤ x ≤ ub .

Internamente, ga converte un array lb nell'array lb(:).

Esempio lb = [0;-Inf;4] significa x(1) ≥ 0, x(3) ≥ 4 .

Tipi di dati: double

ub — Limiti superiori

[] (predefinito) | array o array reale

Limiti superiori, specificati come array reale o array di double. ub rappresenta i limiti superiori elemento per elemento in lb ≤ x ≤ ub.

Internamente, ga converte un array ub nell'array ub(:).

Esempio ub = [Inf;4;10] significa x(2) ≤ 4, x(3) ≤ 10 .

Tipi di dati: double

nonlcon — Vincoli non lineari

funzione handle | nome della funzione

Vincoli non lineari, specificati come funzione handle o nome di funzione. nonlcon è una funzione che accetta un vettore o un array x e restituisce due array, c(x) e ceq(x).

• c(x) è la matrice dei vincoli di disuguaglianza non lineare in x . ga tenta di soddisfare

  c(x) <= 0

  per tutte le voci di c .

• ceq(x) è l'array di vincoli di uguaglianza non lineare in x . ga tenta di soddisfare

  ceq(x) = 0

  per tutte le voci di ceq .

Per esempio,

x = ga(@myfun,4,A,b,Aeq,beq,lb,ub,@mycon)

dove mycon è una funzione MATLAB^® come

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

Per ulteriori informazioni, vedere Nonlinear Constraints .

Per imparare a usare i vincoli vettoriali, vedere Vectorized Constraints .

Nota

ga non impone vincoli non lineari da soddisfare quando l'opzione PopulationType è impostata su 'bitString' o 'custom'.

Se intcon non è vuoto, il secondo output di nonlcon (ceq) deve essere una voce vuota ([]).

Per informazioni su come ga utilizza nonlcon, vedere Nonlinear Constraint Solver Algorithms for Genetic Algorithm.

Tipi di dati: char | function_handle | string

options — Opzioni di ottimizzazione

uscita di optimoptions | struttura

Opzioni di ottimizzazione, specificate come output di optimoptions o come struttura.

optimoptions nasconde le opzioni elencate in corsivo. Vedi Options that optimoptions Hides .

• I valori in {} indicano il valore predefinito.

• {}* rappresenta l'impostazione predefinita quando ci sono vincoli lineari e per MutationFcn anche quando ci sono limiti.

• I* indica l'impostazione predefinita per i vincoli interi oppure indica considerazioni speciali per i vincoli interi.

• NM indica che l'opzione non si applica a gamultiobj .

Opzioni per ga e gamultiobj

Opzione	Descrizione	Valori
ConstraintTolerance	Determina la fattibilità rispetto ai vincoli non lineari. Inoltre, max(sqrt(eps),ConstraintTolerance) determina la fattibilità rispetto ai vincoli lineari. Per una struttura di opzioni, utilizzare TolCon .	Scalare non negativo | {1e-3}
CreationFcn	Funzione che crea la popolazione iniziale. Specificare come nome di una funzione di creazione incorporata o di una funzione handle. Vedi Population Options .	{'gacreationuniform'} | {'gacreationlinearfeasible'}* | 'gacreationnonlinearfeasible' | {'gacreationuniformint'}I* per ga | {'gacreationsobol'}I* per gamultiobj | Funzione di creazione personalizzata
CrossoverFcn	Funzione utilizzata dall'algoritmo per creare children crossover. Specificare come nome una funzione crossover incorporata o una funzione handle. Vedi Crossover Options .	{'crossoverscattered'} per ga, {'crossoverintermediate'}* per gamultiobj | {'crossoverlaplace'}I* | 'crossoverheuristic' | 'crossoversinglepoint' | 'crossovertwopoint' | 'crossoverarithmetic' | Funzione crossover personalizzata
CrossoverFraction	La frazione della popolazione nella generazione successiva, esclusi i children dell'élite, creata dalla funzione di crossover.	Scalare non negativo | {0.8}
Display	Livello di visualizzazione.	'off' | 'iter' | 'diagnose' | {'final'}
DistanceMeasureFcn	Funzione che calcola la misura della distanza degli individui. Specificare come nome una funzione di misura della distanza incorporata o una funzione handle. Il valore si applica alla variabile decisionale o allo spazio di progettazione (genotipo) o allo spazio funzionale (fenotipo). Il valore predefinito 'distancecrowding' si trova nello spazio funzionale (fenotipo). Solo per gamultiobj. Vedi Multiobjective Options . Per una struttura di opzioni, utilizzare una funzione handle, non un nome.	{'distancecrowding'} ha lo stesso significato di {@distancecrowding,'phenotype'} | {@distancecrowding,'genotype'} | Funzione di distanza personalizzata
EliteCount	NM Numero intero positivo che specifica quanti individui della generazione attuale hanno la garanzia di sopravvivere alla generazione successiva. Non utilizzato in gamultiobj .	Intero non negativo | {ceil(0.05*PopulationSize)} | {0.05*(default PopulationSize)} per problemi misti interi
FitnessLimit	NM Se la funzione di fitness raggiunge il valore di FitnessLimit, l'algoritmo si arresta.	Scalare | {-Inf}
FitnessScalingFcn	Funzione che scala i valori della funzione di fitness. Specificare come nome di una funzione di ridimensionamento integrata o di una funzione handle. Opzione non disponibile per gamultiobj .	{'fitscalingrank'} | 'fitscalingshiftlinear' | 'fitscalingprop' | 'fitscalingtop' | Funzione di ridimensionamento fitness personalizzata
FunctionTolerance	L'algoritmo si arresta se la variazione relativa media del valore della migliore funzione di fitness su MaxStallGenerations generazioni è minore o uguale a FunctionTolerance. Se StallTest è 'geometricWeighted', l'algoritmo si arresta se la variazione relativa media ponderata è minore o uguale a FunctionTolerance. Per gamultiobj, l'algoritmo si arresta quando la media geometrica della variazione relativa del valore dello spread su options.MaxStallGenerations generazioni è inferiore a options.FunctionTolerance e lo spread finale è inferiore allo spread medio sulle ultime options.MaxStallGenerations generazioni. Vedi gamultiobj Algorithm . Per una struttura di opzioni, utilizzare TolFun .	Scalare non negativo | {1e-6} per ga, {1e-4} per gamultiobj
HybridFcn	I* Funzione che continua l'ottimizzazione dopo la terminazione di ga. Specificare come nome o funzione handle. In alternativa, un array di celle che specifica la funzione ibrida e le sue opzioni. Vedi ga Hybrid Function . Per gamultiobj, l'unica funzione ibrida è @fgoalattain. Vedi gamultiobj Hybrid Function . Quando il problema presenta vincoli interi, non è possibile utilizzare una funzione ibrida. Vedi Quando utilizzare una funzione ibrida .	Nome funzione o handle | 'fminsearch' | 'patternsearch' | 'fminunc' | 'fmincon' | {[]} O Matrice di celle 1 per 2 | {@solver, hybridoptions}, dove solver = fminsearch, patternsearch, fminunc o fmincon {[]}
Penalità Iniziale	NM I* Valore iniziale del parametro di penalità	Scalare positivo | {10}
InitialPopulationMatrix	Popolazione iniziale utilizzata per generare l'algoritmo genetico. Ha fino a PopulationSize righe e N colonne, dove N è il numero di variabili. È possibile passare una popolazione parziale, ovvero una con meno di PopulationSize righe. In tal caso, l'algoritmo genetico utilizza CreationFcn per generare i membri rimanenti della popolazione. Vedi Population Options . Per una struttura di opzioni, utilizzare InitialPopulation .	Matrice | {[]}
InitialPopulationRange	Matrice o vettore che specifica l'intervallo degli individui nella popolazione iniziale. Si applica alla funzione di creazione gacreationuniform. ga sposta e ridimensiona l'intervallo iniziale predefinito per adattarlo a eventuali limiti finiti. Per una struttura di opzioni, utilizzare PopInitRange .	Matrice o vettore | {[-10;10]} per componenti illimitate, {[-1e4+1;1e4+1]} per componenti illimitate di problemi con vincoli interi, {[lb;ub]} per componenti limitate, con l'intervallo predefinito modificato per corrispondere ai limiti unilaterali
InitialScoresMatrix	Punteggi iniziali utilizzati per determinare l'idoneità. Ha fino a PopulationSize righe e Nf colonne, dove Nf è il numero di funzioni di fitness (1 per ga, maggiore di 1 per gamultiobj). È possibile passare una matrice di punteggi parziali, ovvero una con meno di PopulationSize righe. In tal caso, il risolutore inserisce i punteggi quando valuta le funzioni di idoneità. Per una struttura di opzioni, utilizzare InitialScores .	Vettore colonna per obiettivo singolo | matrice per multiobiettivo | {[]}
MaxGenerations	Numero massimo di iterazioni prima che l'algoritmo si arresti. Per una struttura di opzioni, utilizzare Generations .	Intero non negativo |{100*numberOfVariables} per ga, {200*numberOfVariables} per gamultiobj
MaxStallGenerations	L'algoritmo si arresta se la variazione relativa media del valore della migliore funzione di fitness su MaxStallGenerations generazioni è minore o uguale a FunctionTolerance. Se StallTest è 'geometricWeighted', l'algoritmo si arresta se la variazione relativa media ponderata è minore o uguale a FunctionTolerance. Per gamultiobj, l'algoritmo si arresta quando la media geometrica della variazione relativa del valore dello spread su options.MaxStallGenerations generazioni è inferiore a options.FunctionTolerance e lo spread finale è inferiore allo spread medio sulle ultime options.MaxStallGenerations generazioni. Vedi gamultiobj Algorithm . Per una struttura di opzioni, utilizzare StallGenLimit .	Intero non negativo | {50} per ga, {100} per gamultiobj
MaxStallTime	NM L'algoritmo si arresta se non si verifica alcun miglioramento nella funzione obiettivo per MaxStallTime secondi, come misurato da tic e toc. Per una struttura di opzioni, utilizzare StallTimeLimit .	Scalare positivo | {Inf}
MaxTime	L'algoritmo si arresta dopo un'esecuzione di MaxTime secondi, come misurato da tic e toc. Questo limite viene applicato dopo ogni iterazione, quindi ga può superarlo quando un'iterazione richiede molto tempo. Per una struttura di opzioni, utilizzare TimeLimit .	Scalare non negativo | {Inf}
Direzione della migrazione	Direzione della migrazione. Vedi Migration Options .	'both' | {'forward'}
Frazione di Migrazione	Scalare da 0 a 1 che specifica la frazione di individui in ciascuna sottopopolazione che migra verso una sottopopolazione diversa. Vedi Migration Options .	Scalare | {0.2}
Intervallo di migrazione	Numero intero positivo che specifica il numero di generazioni che hanno luogo tra le migrazioni di individui tra sottopopolazioni. Vedi Migration Options .	Numero intero positivo | {20}
MutationFcn	Funzione che produce mutation children. Specificare come nome una funzione di mutation incorporata o una funzione handle. Vedi Mutation Options .	{'mutationgaussian'} per ga senza vincoli | {'mutationadaptfeasible'}* per gamultiobj e per ga con vincoli | {'mutationpower'}I* | 'mutationpositivebasis' | 'mutationuniform' | Funzione di mutation personalizzata.
NonlinearConstraintAlgorithm	Algoritmo di vincolo non lineare. Vedi Nonlinear Constraint Solver Algorithms for Genetic Algorithm . Opzione non modificabile per gamultiobj . Per una struttura di opzioni, utilizzare NonlinConAlgorithm .	{'auglag'} per ga, {'penalty'} per gamultiobj
OutputFcn	Funzioni che ga richiama a ogni iterazione. Specificare come funzione handle o come array di celle di funzione handle. Vedi Output Function Options . Per una struttura di opzioni, utilizzare OutputFcns .	Funzione handle o array di celle di funzione handle | {[]}
ParetoFraction	Scalare da 0 a 1 che specifica la frazione di individui da mantenere sul primo fronte di Pareto mentre il risolutore seleziona gli individui dai fronti superiori, solo per gamultiobj. Vedi Multiobjective Options .	Scalare | {0.35}
Penalty Factor	NM I* Parametro di aggiornamento della penalità.	Scalare positivo | {100}
PlotFcn	Funzione che traccia i dati elaborati dall'algoritmo. Specificare come nome una funzione di grafico incorporata, una funzione handle o una matrice di celle di nomi incorporati o funzioni handle. Vedi Plot Options . Per una struttura di opzioni, utilizzare PlotFcns .	ga oppure gamultiobj: {[]} | 'gaplotdistance' | 'gaplotgenealogy' | 'gaplotselection' | 'gaplotscorediversity' |'gaplotscores' | 'gaplotstopping' | 'gaplotmaxconstr' | Funzione di tracciamento personalizzata Solo ga: 'gaplotbestf' | 'gaplotbestindiv' | 'gaplotexpectation' | 'gaplotrange' Solo gamultiobj: 'gaplotpareto' | 'gaplotparetodistance' | 'gaplotrankhist' | 'gaplotspread'
Intervallo di Trama	Numero intero positivo che specifica il numero di generazioni tra chiamate consecutive alle funzioni di tracciamento.	Numero intero positivo | {1}
PopulationSize	Dimensione della popolazione.	Intero positivo | {50} quando numberOfVariables <= 5, {200} altrimenti | {min(max(10*nvars,40),100)} per problemi misti interi
PopulationType	Tipo di dati della popolazione. Deve essere 'doubleVector' per i problemi misti interi.	'bitstring' | 'custom' | {'doubleVector'} ga ignora tutti i vincoli quando PopulationType è impostato su 'bitString' o 'custom'. Vedi Population Options .
SelectionFcn	Funzione che seleziona i genitori di crossover e mutation children. Specificare come nome di una funzione di selezione incorporata o di una funzione handle. gamultiobj utilizza solo 'selectiontournament' .	{'selectionstochunif'} per ga, {'selectiontournament'} per gamultiobj | 'selectionremainder' | 'selectionuniform' | 'selectionroulette' | Funzione di selezione personalizzata
Test di Stallo	NM Interruzione del tipo di test.	'geometricWeighted' | {'averageChange'}
UseParallel	Calcolare in parallelo le funzioni di idoneità e di vincolo non lineare. Vedere Vectorize and Parallel Options (User Function Evaluation) e How to Use Parallel Processing in Global Optimization Toolbox .	true | {false}
UseVectorized	Specifica se le funzioni sono vettorializzate. Vedere Vectorize and Parallel Options (User Function Evaluation) e Vectorize the Fitness Function . Per una struttura di opzioni, utilizzare Vectorized con i valori 'on' o 'off' .	true | {false}

Esempio optimoptions('ga','PlotFcn',@gaplotbestf)

intcon — Variabili intere

vettore di numeri interi positivi

Variabili intere, specificate come un vettore di numeri interi positivi che assumono valori da 1 a nvars. Ogni valore in intcon rappresenta un componente x che ha valore intero.

Nota

Se intcon non è vuoto, nonlcon deve restituire vuoto per ceq. Per ulteriori informazioni sulla programmazione intera, vedere Mixed Integer ga Optimization .

Esempio Per specificare che le voci pari in x hanno valore intero, impostare intcon su 2:2:nvars

Tipi di dati: double

problem — Descrizione del problema

struttura

Descrizione del problema, specificata come una struttura contenente questi campi.

fitnessfcn	Funzioni di fitness
nvars	Numero di variabili di progettazione
Aineq	Matrice A per vincoli di disuguaglianza lineare
Bineq	Vettore b per vincoli di disuguaglianza lineare
Aeq	Matrice Aeq per vincoli di uguaglianza lineare
Beq	Vettore beq per vincoli di uguaglianza lineare
lb	Limite inferiore su x
ub	Limite superiore su x
nonlcon	Funzioni di vincolo non lineare
intcon	Indici di variabili intere
rngstate	Campo per reimpostare lo stato del generatore di numeri casuali
solver	'ga'
options	Opzioni create utilizzando optimoptions o una struttura di opzioni

È necessario specificare i campi fitnessfcn, nvars e options. I restanti sono facoltativi per ga .

Tipi di dati: struct

Argomenti di output

x — Soluzione

vettore reale

Soluzione, restituita come vettore reale. x è il punto migliore che ga ha individuato durante le sue iterazioni.

fval — Valore della funzione obiettivo nella soluzione

numero reale

Valore della funzione obiettivo nella soluzione, restituito come numero reale. In genere, fval = fun(x) .

exitflag — Motivo per cui ga si è fermato

numero intero

Motivo per cui ga si è fermato, è stato restituito come un numero intero.

Bandiera di uscita	Significato
1	Senza vincoli non lineari — La variazione cumulativa media del valore della funzione di fitness su MaxStallGenerations generazioni è inferiore a FunctionTolerance e la violazione del vincolo è inferiore a ConstraintTolerance.
	Con vincoli non lineari — L'entità della misura di complementarietà (vedere Misura di complementarietà) è minore di sqrt(ConstraintTolerance), il sottoproblema è risolto utilizzando una tolleranza minore di FunctionTolerance e la violazione del vincolo è minore di ConstraintTolerance.
3	Il valore della funzione di fitness non è cambiato in MaxStallGenerations generazioni e la violazione del vincolo è minore di ConstraintTolerance.
4	L'entità del passo è inferiore alla precisione della macchina e la violazione del vincolo è inferiore a ConstraintTolerance.
5	È stato raggiunto il limite minimo di idoneità FitnessLimit e la violazione del vincolo è inferiore a ConstraintTolerance.
0	Superato il numero massimo di generazioni MaxGenerations.
-1	Ottimizzazione terminata da una funzione di output o da una funzione di grafico.
-2	Non è stato trovato alcun punto fattibile.
-4	Superato il limite di tempo di stallo MaxStallTime.
-5	Limite di tempo MaxTime superato.

In presenza di vincoli interi, ga utilizza il valore di idoneità della penalità anziché il valore di idoneità per i criteri di arresto.

output — Informazioni sul processo di ottimizzazione

struttura

Informazioni sul processo di ottimizzazione, restituite come una struttura con questi campi:

• problemtype — Tipo di problema, uno dei:

  • 'unconstrained'

  • 'boundconstraints'

  • 'linearconstraints'

  • 'nonlinearconstr'

  • 'integerconstraints'

• rngstate — Stato del generatore di numeri casuali MATLAB, appena prima dell'avvio dell'algoritmo. È possibile utilizzare i valori in rngstate per riprodurre l'output di ga . Vedi Reproduce Results .

• generations — Numero di generazioni calcolate.

• funccount — Numero di valutazioni della funzione di fitness.

• message — Motivo per cui l'algoritmo è terminato.

• maxconstraint — Violazione massima del vincolo, se presente.

• hybridflag — Flag di uscita dalla funzione ibrida. Si riferisce a HybridFcn options . Non applicabile a gamultiobj .

population — Popolazione finale

matrice

Popolazione finale, restituita come matrice PopulationSize-by-nvars. Le righe di population sono gli individui.

scores — Punteggi finali

vettore colonna

Punteggi finali, restituiti come vettore colonna.

• Per i problemi non interi, i punteggi finali sono i valori della funzione di idoneità delle righe di population .

• Per i problemi interi, i punteggi finali sono i valori di idoneità di penalità dei membri della popolazione. Vedi Integer ga Algorithm .

Ulteriori informazioni

Misura di complementarietà

Nel risolutore di vincoli non lineari di Lagrangian aumentato, la misura di complementarietà è la norma del vettore i cui elementi sono c_iλ_i, dove c_i è la violazione del vincolo di disuguaglianza non lineare e λ_i è il moltiplicatore di Lagrange corrispondente. Vedi Augmented Lagrangian Genetic Algorithm .

Suggerimenti

• Per scrivere una funzione con parametri aggiuntivi alle variabili indipendenti che possono essere chiamate da ga, vedere Passing Extra Parameters.

• Per i problemi che utilizzano il tipo di popolazione Double Vector (predefinito), ga non accetta funzioni i cui input sono di tipo complex. Per risolvere problemi che coinvolgono dati complessi, scrivi le tue funzioni in modo che accettino vettori reali, separando la parte reale da quella immaginaria.

Algoritmi

Per una descrizione dell'algoritmo genetico, vedere Come funziona l'algoritmo genetico .

Per una descrizione dell'algoritmo di programmazione mista intera, vedere Integer ga Algorithm .

Per una descrizione degli algoritmi di vincolo non lineare, vedere Nonlinear Constraint Solver Algorithms for Genetic Algorithm .

Funzionalità alternativa

Applicazione

L'attività Ottimizza Live Editor fornisce un'interfaccia visiva per ga .

Riferimenti

[1] Goldberg, David E., Genetic Algorithms in Search, Optimization & Machine Learning, Addison-Wesley, 1989.

[2] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds”, SIAM Journal on Numerical Analysis, Volume 28, Number 2, pages 545–572, 1991.

[3] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds”, Mathematics of Computation, Volume 66, Number 217, pages 261–288, 1997.

Funzionalità estese

Supporto parallelo automatico

Accelera il codice mediante esecuzione automatica dei calcoli in parallelo con Parallel Computing Toolbox™.

Per l'esecuzione in parallelo, impostare l'opzione 'UseParallel' su true.

options = optimoptions('solvername','UseParallel',true)

Per ulteriori informazioni, vedere How to Use Parallel Processing in Global Optimization Toolbox .

Cronologia versioni

Introduzione prima di R2006a

R2019b: ga esegue meno valutazioni della funzione di fitness

Quando la funzione di fitness è deterministica, ga non rivaluta la funzione di fitness sugli individui d'élite (i migliori al momento). È possibile controllare questo comportamento accedendo al nuovo campo state.EvalElites e modificandolo in una funzione di output personalizzata o in una funzione di grafico personalizzata. Allo stesso modo, quando la popolazione iniziale presenta membri duplicati, ga valuta ogni membro univoco solo una volta. È possibile controllare questo comportamento in una funzione di output personalizzata o in una funzione di grafico personalizzata accedendo e modificando il nuovo campo state.HaveDuplicates. Per maggiori dettagli, vedere Custom Output Function for Genetic Algorithm o Funzione grafico personalizzata.

Per maggiori dettagli sui due nuovi campi, vedere The State Structure .

Vedi anche

gamultiobj | optimoptions | particleswarm | patternsearch | Ottimizzare

Argomenti

• Algoritmo genetico
• Inizia con Global Optimization Toolbox
• Impostazione del problema di ottimizzazione basata sul risolutore