meshz
Mesh surface plot with curtain
Description
meshz(
creates a mesh plot with a curtain around it. A mesh plot is a three-dimensional
surface that has solid edge colors and no face colors. The function plots the
values in matrix X,Y,Z)Z as heights above a grid in the
x-y plane defined by
X and Y. The edge colors vary
according to the heights specified by Z.
meshz( creates a mesh plot with a
curtain, and uses the column and row indices of the elements in
Z)Z as the x- and
y-coordinates.
meshz(___,
specifies additional options for the Name,Value)meshz plot using one or
more name-value pair arguments. Specify the options after all other input
arguments. For a list of properties, see Surface Properties.
meshz( plots into
the axes specified by ax,___)ax instead of the current axes. Specify
the axes as the first input argument.
s = meshz(___) returns the chart surface
object. Use s to modify the mesh plot after it is created.
For a list of properties, see Surface Properties.
Examples
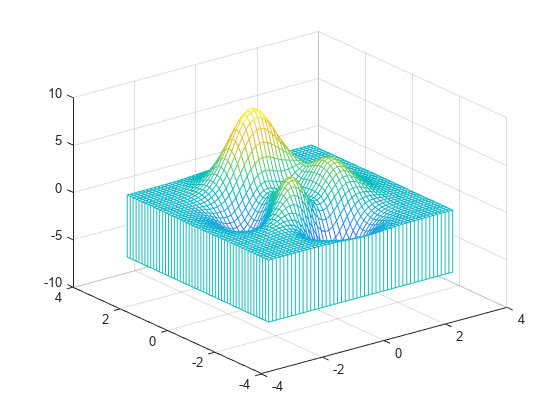
Create three matrices of the same size. Then plot them as a mesh plot with a curtain. The mesh plot uses Z for both height and color.
[X,Y] = meshgrid(-3:.125:3); Z = peaks(X,Y); meshz(X,Y,Z)
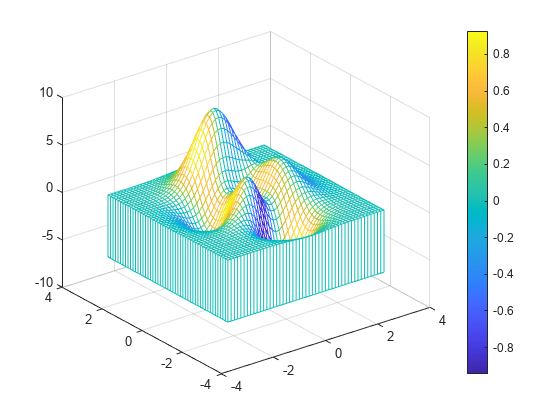
Specify the colors for a mesh plot and surrounding curtain by including a fourth matrix input, C. The mesh plot uses Z for height and C for color. Specify the colors using a colormap, which uses single numbers to stand for colors on a spectrum. When you use a colormap, C is the same size as Z. Add a color bar to the graph to show how the data values in C correspond to the colors in the colormap.
[X,Y] = meshgrid(-3:.125:3); Z = peaks(X,Y); C = gradient(Z); meshz(X,Y,Z,C) colorbar
Create a mesh plot with a curtain around it. To allow further modifications, assign the surface object to the variable s.
[X,Y] = meshgrid(-5:.5:5); Z = Y.*sin(X) - X.*cos(Y); s = meshz(X,Y,Z)
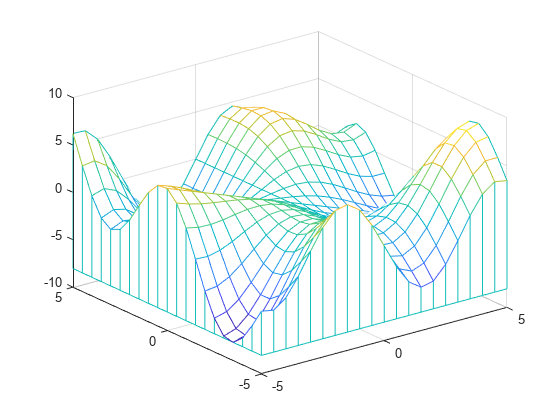
s =
Surface (meshz) with properties:
EdgeColor: 'flat'
LineStyle: '-'
FaceColor: [1 1 1]
FaceLighting: 'none'
FaceAlpha: 1
XData: [25×25 double]
YData: [25×25 double]
ZData: [25×25 double]
CData: [25×25 double]
Show all properties
Use s to access and modify properties of the mesh plot after it is created. For example, change the color of the mesh plot edges and surrounding curtain by setting the EdgeColor property.
s.EdgeColor = 'b';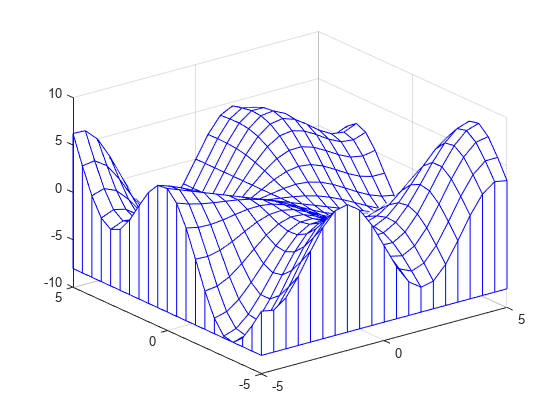
Input Arguments
x-coordinates, specified as a matrix the same size as
Z, or as a vector with length n,
where [m,n] = size(Z). If you do not specify values for
X and Y,
meshz uses the vectors (1:n) and
(1:m).
When X is a matrix, the values must be strictly
increasing or decreasing along one dimension and remain constant along the
other dimension. The dimension that varies must be the opposite of the
dimension that varies in Y. You can use the meshgrid function to create
X and Y matrices.
When X is a vector, the values must be strictly
increasing or decreasing.
The XData property of the surface object stores the
x-coordinates.
Example: X = 1:10
Example: X = [1 2 3; 1 2 3; 1 2 3]
Example: [X,Y] = meshgrid(-5:0.5:5)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical
y-coordinates, specified as a matrix the same size as
Z or as a vector with length m,
where [m,n] = size(Z). If you do not specify values for
X and Y,
meshz uses the vectors (1:n) and
(1:m).
When Y is a matrix, the values must be strictly
increasing or decreasing along one dimension and remain constant along the
other dimension. The dimension that varies must be the opposite of the
dimension that varies in X. You can use the meshgrid function to create
X and Y matrices.
When Y is a vector, the values must be strictly
increasing or decreasing.
The YData property of the surface object stores the
y-coordinates.
Example: Y = 1:10
Example: Y = [1 1 1; 2 2 2; 3 3 3]
Example: [X,Y] = meshgrid(-5:0.5:5)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical
z-coordinates, specified as a matrix.
Z must have at least two rows and two columns.
Z specifies the height of the mesh plot at each
x-y coordinate. If you do not
specify the colors, then Z also specifies the mesh edge
colors.
The ZData property of the surface object stores the
z-coordinates.
Example: Z = [1 2 3; 4 5 6]
Example: Z = sin(x) + cos(y)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical
Color array, specified as an m-by-n matrix of colormap indices, where
Z is m-by-n.
For each grid point on the mesh surface, C indicates a
color in the colormap. The CDataMapping property of the
surface object controls how the values in C correspond to
colors in the colormap.
The CData property of the surface object stores the
color array. For additional control over the surface coloring, use the
FaceColor and EdgeColor
properties.
Axes to plot in, specified as an axes object. If you do
not specify the axes, then meshz plots into the current
axes.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: meshz(X,Y,Z,'EdgeColor','red') creates the mesh with
red lines.
Note
The properties listed here are only a subset. For a full list, see Surface Properties.
Edges to display, specified as 'both', 'row',
or 'column'.
Edge line color, specified as one of the values listed in this table.
| Value | Description |
|---|---|
'none' | Do not draw the edges. |
'flat' | Use a different color for each edge based on the values
in the
|
'interp' |
Use interpolated coloring for each edge based on the values in the
|
| RGB triplet, hexadecimal color code, or color name |
Use the specified color for all the edges. This option does not use the color
values in the
|
RGB triplets and hexadecimal color codes are useful for specifying custom colors.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7].A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Thus, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Face color, specified as one of the values in this table.
| Value | Description |
|---|---|
'flat' | Use a different color for each face based on the values
in the
|
'interp' |
Use interpolated coloring for each face based on the values in the
|
| RGB triplet, hexadecimal color code, or color name |
Use the specified color for all the faces. This option does not use the color
values in the
|
'texturemap' | Transform the color data in CData so that
it conforms to the surface. |
'none' | Do not draw the faces. |
RGB triplets and hexadecimal color codes are useful for specifying custom colors.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7].A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Thus, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Edge transparency, specified as one of these values:
Scalar in range
[0,1]— Use uniform transparency across all of the edges. A value of1is fully opaque and0is completely transparent. Values between0and1are semitransparent. This option does not use the transparency values in theAlphaDataproperty.'flat'— Use a different transparency for each edge based on the values in theAlphaDataproperty. First you must specify theAlphaDataproperty as a matrix the same size as theZDataproperty. The transparency value at the first vertex determines the transparency for the entire edge. TheEdgeColorproperty also must be set to'flat'.'interp'— Use interpolated transparency for each edge based on the values inAlphaDataproperty. First you must specify theAlphaDataproperty as a matrix the same size as theZDataproperty. The transparency varies across each edge by interpolating the values at the vertices. TheEdgeColorproperty also must be set to'interp'.
Line style, specified as one of the options listed in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
"none" | No line | No line |
Line width, specified as a positive value in points, where 1 point = 1/72 of an inch. If the line has markers, then the line width also affects the marker edges.
The line width cannot be thinner than the width of a pixel. If you set the line width to a value that is less than the width of a pixel on your system, the line displays as one pixel wide.
Extended Capabilities
The meshz function
supports GPU array input with these usage notes and limitations:
This function accepts GPU arrays, but does not run on a GPU.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Usage notes and limitations:
This function operates on distributed arrays, but executes in the client MATLAB®.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
See Also
Functions
Properties
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)





