Questa pagina è stata tradotta con la traduzione automatica. Fai clic qui per vedere l'ultima versione in inglese.

plannerAStarGrid

A* pianificatore di percorsi per mappa a griglia

Descrizione

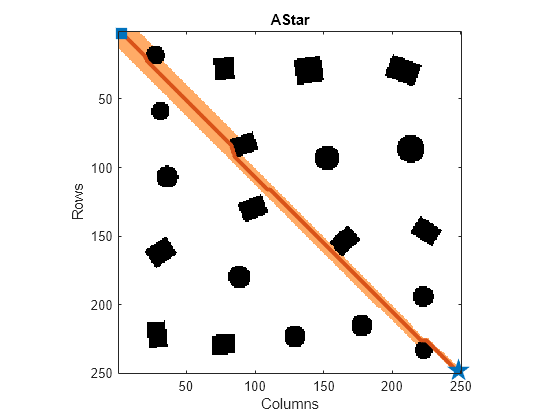
L'oggetto plannerAStarGrid crea un pianificatore di percorsi A*. Il pianificatore esegue una ricerca A* su una mappa di occupazione e trova il percorso più breve e privo di ostacoli tra le posizioni di partenza e di arrivo specificate nella griglia, come determinato dal costo euristico.

Creazione

Sintassi

planner = plannerAStarGrid

planner = plannerAStarGrid(map)

planner = plannerAStarGrid(___,Name,Value)

Descrizione

planner = plannerAStarGrid crea un oggetto plannerAStarGrid con un oggetto binaryOccupancyMap utilizzando una larghezza e un'altezza di 10 metri e una risoluzione della griglia di 1 cella per metro.

planner = plannerAStarGrid(map) crea un oggetto plannerAStarGrid utilizzando l'oggetto mappa specificato map. Specificare map come oggetto binaryOccupancyMap o occupancyMap. L'input map imposta il valore della proprietà Map.

planner = plannerAStarGrid(___,Name,Value) imposta Proprietà utilizzando una o più coppie nome-valore. Le proprietà non specificate hanno valori predefiniti. Racchiudere ogni nome di proprietà tra virgolette.

Ad esempio, plannerAStarGrid(map,'GCost','Manhattan') crea un oggetto pianificatore di percorsi A* utilizzando la funzione di costo Manhattan.

Proprietà

Map — Rappresentazione della mappa

Oggetto binaryOccupancyMap (predefinito) | Oggetto occupancyMap

Rappresentazione della mappa, specificata come oggetto binaryOccupancyMap o occupancyMap. Questo oggetto rappresenta l'ambiente del robot come una griglia di occupazione. Il valore di ogni cella della griglia indica l'occupazione della posizione associata sulla mappa.

Esempio planner.Map = binaryOccupancyMap(zeros(50,50));

GCost — Costo generale dello spostamento tra due punti qualsiasi nella griglia

'Euclidean' (predefinito) | 'Chebyshev' | 'EuclideanSquared' | 'Manhattan'

Il costo generale dello spostamento tra due punti qualsiasi in una griglia, specificato come una delle seguenti funzioni di costo predefinite 'Chebyshev', 'Euclidean', 'EuclideanSquared' o 'Manhattan'.

Il costo dello spostamento tra due punti con coordinate cartesiane (x₁,y₁) e (x₂,y₂) viene calcolato come segue:

• Chebyshev

  $$d=\max \left(\left|{{\displaystyle x}}_2-{{\displaystyle x}}_1\right|,\left|{{\displaystyle y}}_2-{{\displaystyle y}}_1\right|\right)$$

• Euclidean

  $$d=\sqrt{{{\displaystyle \left({{\displaystyle x}}_2-{{\displaystyle x}}_1\right)}}^2+{{\displaystyle \left({{\displaystyle y}}_2-{{\displaystyle y}}_1\right)}}^2}$$

• Euclidean Squared

  $$d={{\displaystyle \left({{\displaystyle x}}_2-{{\displaystyle x}}_1\right)}}^2+{{\displaystyle \left({{\displaystyle y}}_2-{{\displaystyle y}}_1\right)}}^2$$

• Manhattan

  $$d=\left|{{\displaystyle x}}_2-{{\displaystyle x}}_1\right|+\left|{{\displaystyle y}}_2-{{\displaystyle y}}_1\right|$$

Nota

È possibile utilizzare le funzioni di costo predefinite oppure una funzione di costo personalizzata. Per utilizzare una funzione di costo personalizzata, vedere la proprietà GCostFcn.

Esempio planner = plannerAStarGrid(map,'GCost','Manhattan');

Esempio planner.GCost = 'Chebyshev';

Tipi di dati: string | char

GCostFcn — Funzione GCost personalizzata

funzione handle

Funzione GCost personalizzata, specificata come funzione handle. La funzione handle deve accettare due input di posa come vettori [row column] e restituire uno scalare di tipo double.

Nota

È possibile utilizzare le funzioni di costo predefinite oppure una funzione di costo personalizzata. Per utilizzare le funzioni di costo predefinite, vedere la proprietà GCost.

Esempio planner = plannerAStarGrid(map,'GCostFcn',@(pose1,pose2)sum(abs(pose1-pose2),2));

Esempio planner.GCostFcn = @(pose1,pose2)sum(abs(pose1-pose2),2);

Tipi di dati: function_handle

HCost — Costo euristico tra punto e obiettivo nella griglia

'Euclidean' (predefinito) | 'Chebyshev' | 'EuclideanSquared' | 'Manhattan'

Il costo euristico tra un punto e l'obiettivo in una griglia, specificato come una delle seguenti funzioni di costo predefinite 'Chebyshev', 'Euclidean', 'EuclideanSquared' o 'Manhattan'.

Il costo dello spostamento tra due punti con coordinate cartesiane (x₁,y₁) e (x₂,y₂) viene calcolato come segue:

• Chebyshev

  $$d=\max \left(\left|{{\displaystyle x}}_2-{{\displaystyle x}}_1\right|,\left|{{\displaystyle y}}_2-{{\displaystyle y}}_1\right|\right)$$

• Euclidean

  $$d=\sqrt{{{\displaystyle \left({{\displaystyle x}}_2-{{\displaystyle x}}_1\right)}}^2+{{\displaystyle \left({{\displaystyle y}}_2-{{\displaystyle y}}_1\right)}}^2}$$

• Euclidean Squared

  $$d={{\displaystyle \left({{\displaystyle x}}_2-{{\displaystyle x}}_1\right)}}^2+{{\displaystyle \left({{\displaystyle y}}_2-{{\displaystyle y}}_1\right)}}^2$$

• Manhattan

  $$d=\left|{{\displaystyle x}}_2-{{\displaystyle x}}_1\right|+\left|{{\displaystyle y}}_2-{{\displaystyle y}}_1\right|$$

Nota

È possibile utilizzare le funzioni di costo predefinite oppure una funzione di costo personalizzata. Per utilizzare una funzione di costo personalizzata, vedere la proprietà HCostFcn.

Esempio planner = plannerAStarGrid(map,'HCost','Manhattan');

Esempio planner.HCost = 'Chebyshev';

Tipi di dati: string | char

HCostFcn — Funzione HCost personalizzata

funzione handle

Funzione HCost personalizzata, specificata come funzione handle. La funzione handle deve accettare due input di posa come vettori [row column] e restituire uno scalare di tipo double.

Nota

È possibile utilizzare le funzioni di costo predefinite oppure una funzione di costo personalizzata. Per utilizzare le funzioni di costo predefinite, vedere la proprietà HCost.

Esempio planner = plannerAStarGrid(map,'HCostFcn',@(pose1,pose2)sum(abs(pose1-pose2),2));

Esempio planner.HCostFcn = @(pose1,pose2)sum(abs(pose1-pose2),2);

Tipi di dati: function_handle

TieBreaker — Attiva/disattiva la modalità spareggio

'off' (predefinito) | 'on'

Attiva/disattiva la modalità tiebreaker, specificata come 'on' o 'off'.

Quando si abilita la proprietà TieBreaker, il pianificatore di percorsi A* sceglie tra più percorsi della stessa lunghezza regolando il valore del costo euristico.

Esempio planner = plannerAStarGrid(map,'TieBreaker','on');

Esempio planner.TieBreaker = 'off';

Tipi di dati: string | char

DiagonalSearch — Attiva/disattiva la modalità di ricerca diagonale

'on' (predefinito) | 'off'

Attiva/disattiva la modalità di ricerca diagonale, specificata come 'on' o 'off'.

Impostando questa proprietà su 'on', il pianificatore di percorsi A* effettua la ricerca in direzione diagonale insieme alle altre quattro direzioni della griglia. Impostando questa proprietà su 'off', il pianificatore di percorsi A* effettua la ricerca solo nelle quattro direzioni della griglia.

Tipi di dati: char | string

Funzioni oggetto

plan	Find shortest obstacle-free path between two points
show	Plot and visualize A* explored nodes and planned path

Esempi

Pianifica un percorso senza ostacoli nella mappa della griglia utilizzando A-Star Path Planner

Pianifica il percorso più breve e privo di collisioni attraverso una mappa a griglia di ostacoli utilizzando l'algoritmo di pianificazione del percorso A*.

Genera un oggetto binaryOccupancyMap con ostacoli sparsi casualmente utilizzando la funzione mapClutter.

rng('default');
map = mapClutter;

Utilizzare la mappa per creare un oggetto plannerAStarGrid.

planner = plannerAStarGrid(map);

Definire i punti di partenza e di arrivo.

start = [2 3];
goal = [248 248];

Pianifica un percorso dal punto di partenza al punto di arrivo.

plan(planner,start,goal);

Visualizza il percorso e i nodi esplorati utilizzando la funzione oggetto show.

show(planner)

Funzionalità estese

Generazione di codice C/C++
Genera codice C e C++ con MATLAB® Coder™.

Cronologia versioni

Introdotto in R2020b

Vedi anche

binaryOccupancyMap | occupancyMap | plannerRRT | plannerRRTStar | plannerHybridAStar