Define Reaction Rates with Enzyme Kinetics
Use differential equations, mass action kinetics, or Michaelis-Menten kinetics to define enzyme reactions.
Simple Model for Single Substrate Catalyzed Reactions
A simple model for enzyme-catalyzed reactions starts a substrate S reversibly
binding with an enzyme E. Some of the substrate
in the substrate/enzyme complex is converted to product P with
the release of the enzyme.
This simple model can be defined with
Differential rate equations. See Enzyme Reactions with Differential Rate Equations.
Reactions with mass action kinetics. See Enzyme Reactions with Mass Action Kinetics.
Reactions with Henri-Michaelis-Menten kinetics. See Enzyme Reactions with Irreversible Henri-Michaelis-Menten Kinetics.
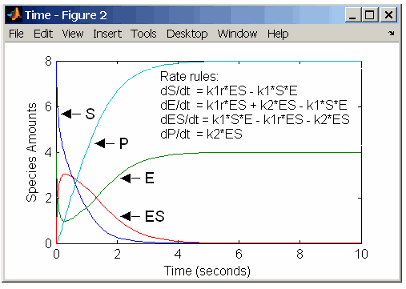
Enzyme Reactions with Differential Rate Equations
The reactions for a single-substrate enzyme reaction mechanism (see Simple Model for Single Substrate Catalyzed Reactions) can be described with differential rate equations. You can enter the differential rate equations into the software as rate rules.
reactions: none
reaction rate: none
rate rules: dS/dt = k1r*ES - k1*S*E
dE/dt = k1r*ES + k2*ES - k1*S*E
dES/dt = k1*S*E - k1r*ES - k2*ES
dP/dt = k2*ES
species: S = 8 mole
E = 4 mole
ES = 0 mole
P = 0 mole
parameters: k1 = 2 1/(mole*second)
k1r = 1 1/second
k2 = 1.5 1/secondRemember that the rate rule dS/dt = f(x) is
written in a SimBiology® rate rule expression as S =
f(x). For more information about rate rules see Rate Rules.
Alternatively, you could remove the rate rule for ES,
add a new species Etotal for the total amount of
enzyme, and add an algebraic rule 0 = Etotal - E - ES,
where the initial amounts for Etotal and E are
equal.
reactions: none
reaction rate: none
rate rules: dS/dt = k1r*ES - k1*S*E
dE/dt = k1r*ES + k2*ES - k1*S*E
dP/dt = k2*ES
algebraic rule: 0 = Etotal - E - ES
species: S = 8 mole
E = 4 mole
ES = 0 mole
P = 0 mole
Etotal = 4 mole
parameters: k1 = 2 1/(mole*second)
k1r = 1 1/second
k2 = 1.5 1/secondEnzyme Reactions with Mass Action Kinetics
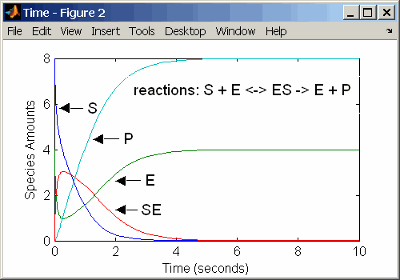
Determining the differential rate equations for the reactions in a model is a time-consuming process. A better way is to enter the reactions for a single substrate enzyme reaction mechanism directly into the software. The following example using models an enzyme catalyzed reaction with mass action kinetics. For a description of the reaction model, see Simple Model for Single Substrate Catalyzed Reactions.
reaction: S + E -> ES
reaction rate: k1*S*E (binding)
reaction: ES -> S + E
reaction rate: k1r*ES (unbinding)
reaction: ES -> E + P
reaction rate: k2*ES (transformation)
species: S = 8 mole
E = 4 mole
ES = 0 mole
P = 0 mole
parameters: k1 = 2 1/(mole*second)
k1r = 1 1/second
k2 = 1.5 1/secondThe results for a simulation using reactions are identical to the results from using differential rate equations.
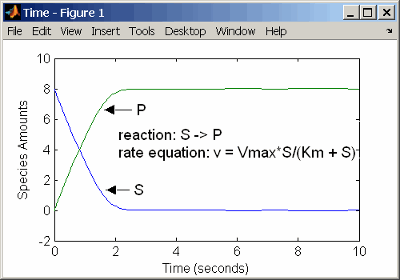
Enzyme Reactions with Irreversible Henri-Michaelis-Menten Kinetics
Representing an enzyme-catalyzed reaction with mass action kinetics
requires you to know the rate constants k1, k1r,
and k2. However, these rate constants are rarely
reported in the literature. It is more common to give the rate constants
for Henri-Michaelis-Menten kinetics with the maximum velocity Vm=k2*E and
the constant Km = (k1r + k2)/k1.
The reaction rate for a single substrate enzyme reaction using Henri-Michaelis-Menten
kinetics is given below. For information about the model, see Simple Model for Single Substrate Catalyzed Reactions.
The following example models an enzyme catalyzed reaction using Henri-Michaelis-Menten kinetics with a single reaction and reaction rate equation. Enter the reaction defined below into the software and simulate.
reaction: S -> P
reaction rate: Vmax*S/(Km + S)
species: S = 8 mole
P = 0 mole
parameters: Vmax = 6 mole/second
Km = 1.25 moleThe results show a plot slightly different from the plot using mass action kinetics. The differences are due to assumptions made when deriving the Michaelis-Menten rate equation.