La traduzione di questa pagina non è aggiornata. Fai clic qui per vedere l'ultima versione in inglese.

Sincronizzazione schiacciata della wavelet

Che cos'è la sincronizzazione schiacciata della wavelet?

La trasformata wavelet sincrona schiacciata è un metodo di analisi tempo-frequenza utile per analizzare segnali multicomponente con modi oscillanti. Esempi di segnali con modi oscillanti sono le forme d'onda del parlato, le vibrazioni delle macchine e i segnali fisiologici. Molti di questi segnali reali con modi oscillanti possono essere scritti come una somma di componenti modulati in ampiezza e in frequenza. Un’espressione generale per questi tipi di segnali con componenti sommati è

$${\displaystyle \sum _{k=1}^K{A}_k(t)\cos (2\pi {\varphi }_k(t))},$$

dove $$A_k(t)$$ è l'ampiezza che varia lentamente e $${\varphi }_k(t)$$ è la fase istantanea. Una serie di Fourier troncata, in cui l'ampiezza e la frequenza non variano nel tempo, è un caso speciale di questi segnali.

La trasformata wavelet e altri metodi di analisi tempo-frequenza lineari scompongono questi segnali nei loro componenti correlando il segnale con un dizionario di atomi tempo-frequenza [1]. La trasformata wavelet utilizza versioni traslate e scalate di una wavelet madre come suo atomo tempo-frequenza. A tutti questi atomi tempo-frequenza è associata una certa estensione temporale che influisce sulla nitidezza dell'analisi del segnale.

La trasformata wavelet sincrona schiacciata è un metodo tempo-frequenza che riassegna l'energia del segnale in frequenza. Questa riassegnazione compensa gli effetti di diffusione causati dalla wavelet madre. A differenza di altri metodi di riassegnazione tempo-frequenza, la sincronizzazione schiacciata riassegna l'energia solo nella direzione della frequenza, preservando la risoluzione temporale del segnale. Preservando il tempo, l'algoritmo di sincronizzazione schiacciata inverso può ricostruire una rappresentazione accurata del segnale originale. Per utilizzare la sincronizzazione schiacciata, ciascun termine dell'espressione del segnale dei componenti sommati deve essere una funzione di tipo intrinseco (IMT). Per i dettagli sui criteri che costituiscono gli IMT, vedere [2].

Algoritmo di sincronizzazione schiacciata della wavelet

L'algoritmo di sincronizzazione schiacciata utilizza le seguenti fasi.

1. Scegliere una wavelet analitica $$\psi (t)$$. Per essere utilizzata con la sincronizzazione schiacciata, la CWT deve utilizzare una wavelet a valore complesso per catturare le informazioni sulla frequenza istantanea.

2. Utilizzare la wavelet per ottenere la CWT del segnale di input $$f(t)$$: $$W_{\psi }f(s,u)$$. Le variabili s e u indicano rispettivamente i parametri di scala e di traslazione.

3. Estrarre le frequenze istantanee dall’output della CWT, utilizzando una trasformata di fase $${\omega }_f$$. Questa trasformata di fase è proporzionale alla derivata prima della CWT rispetto a u.

   $${\omega }_f(s,u)=-i{\left[2\pi W_{\psi }f(s,u)\right]}^{-1}\frac{\partial }{\partial u}{W}_{\psi }f(s,u).$$

   Le scale sono definite come $$s=\frac{{\omega }_0}{\omega }$$, dove $${\omega }_0$$ è il picco di frequenza della wavelet e ω è la frequenza.

4. “Schiacciare” la CWT sulle regioni in cui la trasformata di fase è costante. Il valore della frequenza istantanea risultante è riassegnato a un singolo valore al centro della regione tempo-frequenza della CWT. Questa riassegnazione restituisce un’uscita maggiormente nitida della trasformata sincrona schiacciata rispetto alla CWT.

Come descritto, la sincronizzazione schiacciata utilizza la trasformata wavelet continua (CWT) e la sua derivata prima rispetto alla traslazione. La CWT è invertibile e poiché la trasformata sincrona schiacciata eredita la proprietà di invertibilità della CWT, il segnale può essere ricostruito.

Illustrazione: estrazione di frequenza istantanea

È possibile esprimere la CWT della funzione $$f(t)$$ in relazione alla wavelet $$\psi (t)$$, in termini di trasformata di Fourier inversa del prodotto della trasformata di Fourier della funzione e della trasformata di Fourier della wavelet:

$$W_{\psi }f(s,u)={\displaystyle \int e^{2\pi i\omega u}}\widehat{f}(\omega )\overline{\widehat{\psi }(s\omega )}d\omega ,$$

dove la barra sopra $$\widehat{\psi }(s\omega )$$ denota il coniugato complesso.

Considerare un semplice esponenziale complesso $$f(t)=e^{2\pi i\alpha t}$$. Per estrarre la frequenza istantanea di $$f(t)$$:

1. Ottenere la trasformata della wavelet della funzione:

   $$W_{\psi }f(s,u)=e^{2\pi i\alpha u}\overline{\widehat{\psi }(s\alpha )},$$

   dove $$\widehat{\psi }(s\alpha )$$ è la trasformata di Fourier della wavelet in $$s\alpha$$.

2. Prendere la derivata parziale dell'equazione precedente rispetto alla traslazione u:

   $$\frac{\partial }{\partial u}{W}_{\psi }f(s,u)=2\pi i\alpha e^{2\pi i\alpha u}\overline{\widehat{\psi }(s\alpha )}.$$

3. Applicare la definizione della trasformata di fase $${\omega }_f(s,u)$$ (passaggio 3 in Algoritmo di sincronizzazione schiacciata della wavelet) per ottenere la frequenza istantanea: $${\omega }_f(s,u)=\alpha$$.

Necessaria separazione dei componenti

Con la sincronizzazione schiacciata i componenti del segnale devono essere IMT ben separati nel piano tempo-frequenza. Se questo requisito è soddisfatto, è possibile tracciare la traiettoria delle frequenze istantanee lungo una curva. Le curve mostrano la posizione dell'energia massima al variare del tempo per ciascuna modalità di segnale. Vedere wsstridge per una descrizione dell'algoritmo delle curve di traiettoria.

Questa disuguaglianza definisce i criteri di separazione richiesti:

$$\left|{\varphi }_k^{\text{'}}(t)-{\varphi }_{k-1}^{\text{'}}(t)\right|\ge \frac{1}{4}\left|{\varphi }_k^{\text{'}}(t)+{\varphi }_{k-1}^{\text{'}}(t)\right|$$

dove $${\varphi }^{\text{'}}$$ è la frequenza istantanea e d è una costante di separazione positiva [2]. Per determinare questa separazione richiesta, supponiamo che una wavelet bump x abbia una trasformata di Fourier con supporto nell’intervallo $$\left[{\epsilon }_x-\Delta ,{\epsilon }_x+\Delta \right]$$. Poiché la wavelet bump ha una frequenza centrale di $$\frac{5}{2\pi }$$ Hz, utilizzare $$\left[\frac{5}{2}\pi -\frac{1}{2},\frac{5}{2}\pi +\frac{1}{2}\right]$$ come intervallo. Quindi risolvere $$\Delta <{\epsilon }_x\frac{d}{1+d}$$ per d per ottenere $$d>\frac{1}{4}$$ per la wavelet bump.

Per dimostrare questo requisito di separazione per la wavelet bump, si consideri un segnale composto da $$\cos (2\pi (0.1t))+\sin ((2\pi (0.2t))$$. Utilizzando la wavelet bump per ottenere la CWT, la fase istantanea del coseno è $${\varphi }_1(t)=0.1t$$ e la frequenza istantanea è la derivata prima, 0,1. Analogamente, per il componente sinusoidale, la frequenza istantanea è 0,2. La disuguaglianza di separazione $$\left|0.1\right|\ge \frac{1}{4}\left|0.3\right|$$, è vera. Pertanto, i due componenti del segnale sono funzioni IMT, sufficientemente separate per poter utilizzare la trasformata sincrona schiacciata.

Se si utilizzano frequenze più alte, come 0,3 e 0,4 per le frequenze istantanee, la disuguaglianza è $$\left|0.1\right|\ge \frac{1}{4}\left|0.7\right|$$, che non è vera. Poiché questi componenti del segnale non sono IMT ben separati, il segnale $$\cos (2\pi (0.3t))+\sin ((2\pi (0.4t))$$ non è appropriato per l’utilizzo della trasformata sincrona schiacciata.

Esempi

Dispersione della CWT rispetto alla trasformata sincrona schiacciata

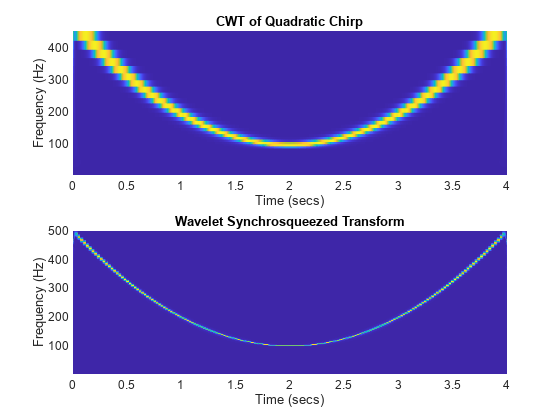
Il confronto tra la CWT e la trasformata sincrona schiacciata di un chirp quadratico mostra una minore dispersione di energia nel risultato della trasformata sincrona schiacciata.

load quadchirp
Fs = 1000;
[wt,f] = cwt(quadchirp,"bump",Fs);
subplot(2,1,1)
hp = pcolor(tquad,f,abs(wt));
hp.EdgeColor = "none";
xlabel("Time (secs)")
ylabel("Frequency (Hz)")
title("CWT of Quadratic Chirp")
subplot(2,1,2)
wsst(quadchirp,Fs,"bump")

Separazione dei componenti a bassa frequenza rispetto ai componenti ad alta frequenza

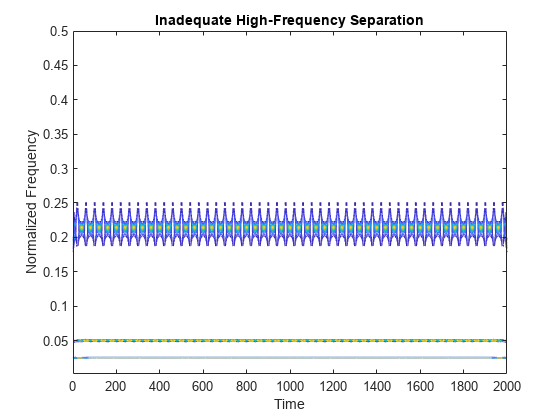
Questo esempio mostra la separazione necessaria tra i componenti del segnale per ottenere risultati utilizzabili dalla trasformata sincrona schiacciata. I componenti del segnale sono 0,025, 0,05, 0,20 e 0,225 cicli per campione. I componenti ad alta frequenza 0,20 e 0,225 non hanno una separazione sufficiente, quindi non è possibile esprimere l'intero segnale come una somma di IMT ben separati.

Definire il segnale e tracciare i componenti sincroni schiacciati.

t = 0:2000;
x1 = cos(2*pi*.025*t);
x2 = cos(2*pi*.05*t);
x3 = cos(2*pi*.20*t);
x4 = cos(2*pi*.225*t);
x =x1+x2+x3+x4;
[sst,f] = wsst(x);
contour(t,f,abs(sst))
xlabel("Time")
ylabel("Normalized Frequency")
title("Inadequate High-Frequency Separation")

Aumentare la separazione dei componenti ad alta frequenza, quindi tracciare nuovamente i componenti sincroni schiacciati.

x4 = cos(2*pi*.3*t);
x =x1+x2+x3+x4;
[sst,f] = wsst(x);
contour(t,f,abs(sst))
xlabel("Time")
ylabel("Normalized Frequency")
title("Adequate High-Frequency Separation")

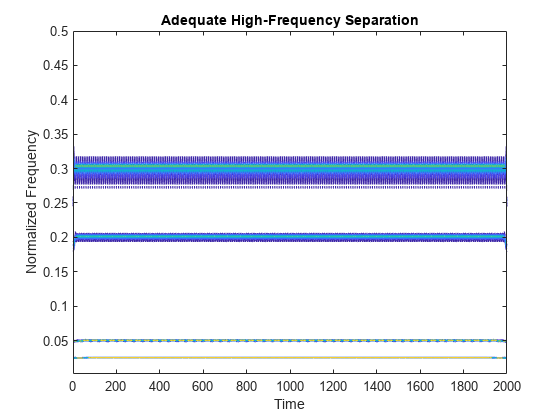
Tutti i componenti del segnale sono ora IMT ben separati e sufficientemente distinti l’uno dall’altro. Questo segnale è adatto per essere utilizzato con l’algoritmo di sincronizzazione schiacciata.

Regione con separazione inadeguata

Questo esempio mostra un segnale con due chirp lineari. Un chirp lineare è definito come

$$f(t)=\cos (\varphi +2\pi (f_{0}t+\frac{m{t}^2}{2})).$$

La sua derivata prima $$f_0+mt$$ definisce la linea di frequenza istantanea. Utilizzare la wavelet bump e la sua costante di separazione di 0,25. Per determinare la regione in cui i due segnali chirp con frequenze istantanee di 0,4 e 0,1 cicli per campione non sono sufficientemente separati, risolvere questa equazione:

$$|y_1-y_2|=0.25|y_1+y_2|.$$

$$y_1=\frac{-0.15}{1000}x+0.4$$ e $$y_2=\frac{0.15}{1000}x+0.1$$ sono le linee di frequenza istantanea dei chirp.

t = 0:2000;
y1 = chirp(t,0.4,1000,0.25);
y2 = chirp(t,0.1,1000,0.25);
y = y1+y2;
wsst(y,'bump')
xlabel('Samples')
h1 = line([583 583], [0 0.5]);
h2 = line([1417 1417], [0 0.5]);
h1.Color='white';
h2.Color='white';

Le linee verticali sono i limiti della regione. Indicano che non si verifica una separazione sufficiente in corrispondenza del campione 583 e del campione 1417. Nella regione tra le linee verticali, il segnale non è costituito da IMT ben separati. Nelle regioni al di fuori delle linee verticali, il segnale presenta IMT ben separati. In queste regioni è possibile ottenere buoni risultati dalla trasformata sincrona schiacciata.

Riferimenti

[1] Mallet, S. A Wavelet Tour of Signal Processing. San Diego, CA: Academic Press, 2008, p. 89.

[2] Daubechies, I., J. Lu, and H. T. Wu. "Synchrosqueezed Wavelet Transforms: an empirical mode decomposition-like tool." Applied and Computational Harmonic Analysis. Vol. 30(2), pp. 243–261.

[3] Thakur, G., E. Brevdo, N. S. Fučkar, and H. T. Wu. "The synchrosqueezing algorithm for time-varying spectral analysis: robustness properties and new paleoclimate applications." Signal Processing. Vol. 93, pp. 1079–1094.

Argomenti complementari

• Time-Frequency Reassignment and Mode Extraction with Synchrosqueezing