Analisi tempo-frequenza
È possibile utilizzare la trasformata wavelet continua (CWT) per analizzare come il contenuto di frequenza di un segnale cambia nel tempo. È possibile eseguire l'analisi adattiva tempo-frequenza utilizzando fotogrammi Gabor non stazionari con trasformata a Q costante (CQT). Per due segnali, la coerenza wavelet rivela modelli comuni variabili nel tempo. È possibile eseguire analisi tempo-frequenza adattive ai dati di processi non lineari e non stazionari. Per le immagini, l'analisi wavelet continua mostra come il contenuto di frequenza di un'immagine varia all'interno dell'immagine e aiuta a rivelare i modelli in un'immagine rumorosa. Per ottenere una risoluzione più nitida ed estrarre i modi di oscillazione da un segnale, è possibile utilizzare la sincronizzazione schiacciata della wavelet.
Utilizzare Wavelet Toolbox™ per eseguire l'analisi tempo-frequenza di segnali e immagini. Con la CQT, è possibile campionare in modo differenziato la larghezza di banda, utilizzando più campioni di frequenza per i componenti a banda larga e meno campioni di frequenza per i componenti a banda stretta. È possibile utilizzare la CWT per ottenere la coerenza wavelet tra due segnali. È possibile scomporre un processo non lineare o non stazionario nei modi di oscillazione intrinseci relativi. È inoltre possibile ricostruire approssimazioni localizzate tempo-frequenza dei segnali. È possibile creare un banco di filtri CWT con intervalli di frequenza o di periodo specifici e applicare in modo efficiente il banco di filtri a più segnali. È possibile visualizzare le wavelet nel tempo e nella frequenza.
Categorie
- Trasformate wavelet continue
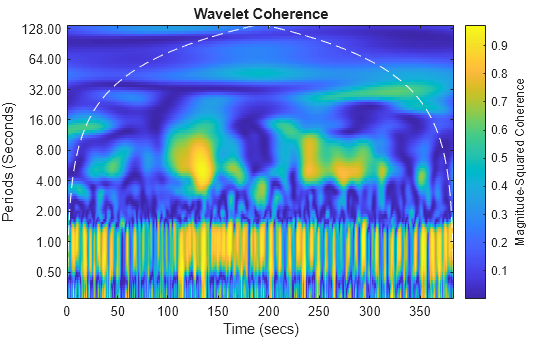
CWT monodimensionali e bidimensionali, CWT inversa monodimensionale, banco di filtri CWT monodimensionale, spettro incrociato e coerenza wavelet
- Trasformate tempo-frequenza a Q costante, adattive ai dati e quadratiche
CQT monodimensionale, CQT inversa monodimensionale, trasformata wavelet empirica, decomposizione in modo empirico, trasformata di Hilbert-Huang, distribuzione di Wigner-Ville