Contenuto principale
Risultati per
The study of the dynamics of the discrete Klein - Gordon equation (DKG) with friction is given by the equation :

above equation, W describes the potential function :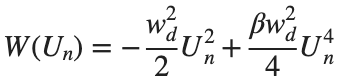
The objective of this simulation is to model the dynamics of a segment of DNA under thermal fluctuations with fixed boundaries using a modified discrete Klein-Gordon equation. The model incorporates elasticity, nonlinearity, and damping to provide insights into the mechanical behavior of DNA under various conditions.
% Parameters
numBases = 200; % Number of base pairs, representing a segment of DNA
kappa = 0.1; % Elasticity constant
omegaD = 0.2; % Frequency term
beta = 0.05; % Nonlinearity coefficient
delta = 0.01; % Damping coefficient
- Position: Random initial perturbations between 0.01 and 0.02 to simulate the thermal fluctuations at the start.
- Velocity: All bases start from rest, assuming no initial movement except for the thermal perturbations.
% Random initial perturbations to simulate thermal fluctuations
initialPositions = 0.01 + (0.02-0.01).*rand(numBases,1);
initialVelocities = zeros(numBases,1); % Assuming initial rest state
The simulation uses fixed ends to model the DNA segment being anchored at both ends, which is typical in experimental setups for studying DNA mechanics. The equations of motion for each base are derived from a modified discrete Klein-Gordon equation with the inclusion of damping:
% Define the differential equations
dt = 0.05; % Time step
tmax = 50; % Maximum time
tspan = 0:dt:tmax; % Time vector
x = zeros(numBases, length(tspan)); % Displacement matrix
x(:,1) = initialPositions; % Initial positions
% Velocity-Verlet algorithm for numerical integration
for i = 2:length(tspan)
% Compute acceleration for internal bases
acceleration = zeros(numBases,1);
for n = 2:numBases-1
acceleration(n) = kappa * (x(n+1, i-1) - 2 * x(n, i-1) + x(n-1, i-1)) ...
- delta * initialVelocities(n) - omegaD^2 * (x(n, i-1) - beta * x(n, i-1)^3);
end
% positions for internal bases
x(2:numBases-1, i) = x(2:numBases-1, i-1) + dt * initialVelocities(2:numBases-1) ...
+ 0.5 * dt^2 * acceleration(2:numBases-1);
% velocities using new accelerations
newAcceleration = zeros(numBases,1);
for n = 2:numBases-1
newAcceleration(n) = kappa * (x(n+1, i) - 2 * x(n, i) + x(n-1, i)) ...
- delta * initialVelocities(n) - omegaD^2 * (x(n, i) - beta * x(n, i)^3);
end
initialVelocities(2:numBases-1) = initialVelocities(2:numBases-1) + 0.5 * dt * (acceleration(2:numBases-1) + newAcceleration(2:numBases-1));
end
% Visualization of displacement over time for each base pair
figure;
hold on;
for n = 2:numBases-1
plot(tspan, x(n, :));
end
xlabel('Time');
ylabel('Displacement');
legend(arrayfun(@(n) ['Base ' num2str(n)], 2:numBases-1, 'UniformOutput', false));
title('Displacement of DNA Bases Over Time');
hold off;
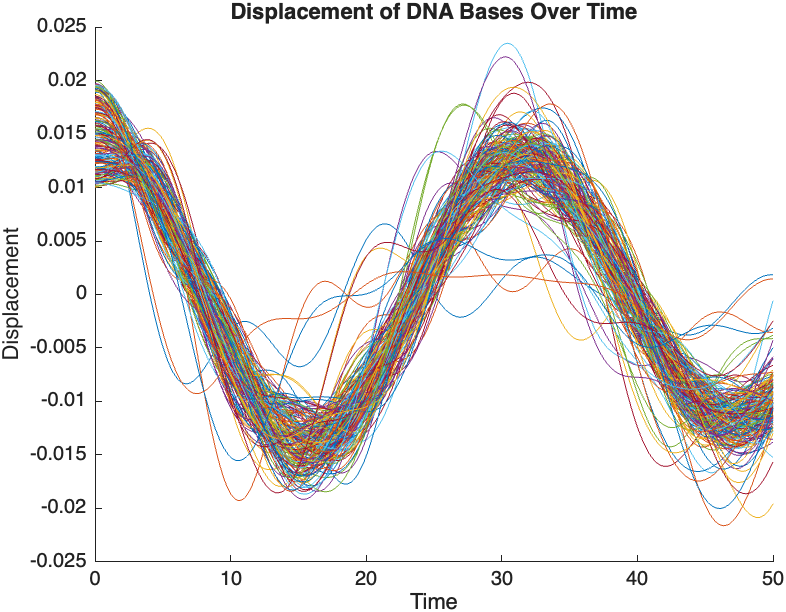
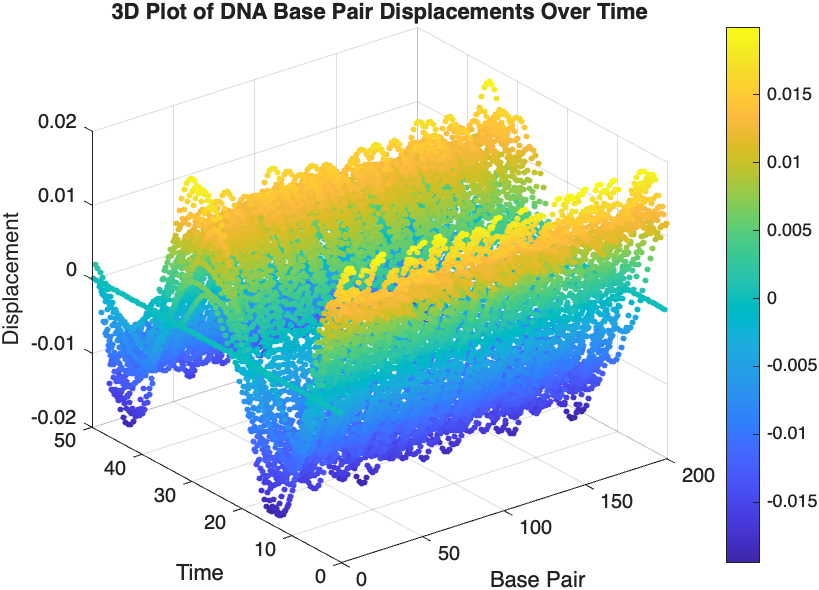
The results are visualized using a plot that shows the displacements of each base over time . Key observations from the simulation include :
- Wave Propagation: The initial perturbations lead to wave-like dynamics along the segment, with visible propagation and reflection at the boundaries.
- Damping Effects: The inclusion of damping leads to a gradual reduction in the amplitude of the oscillations, indicating energy dissipation over time.
- Nonlinear Behavior: The nonlinear term influences the response, potentially stabilizing the system against large displacements or leading to complex dynamic patterns.
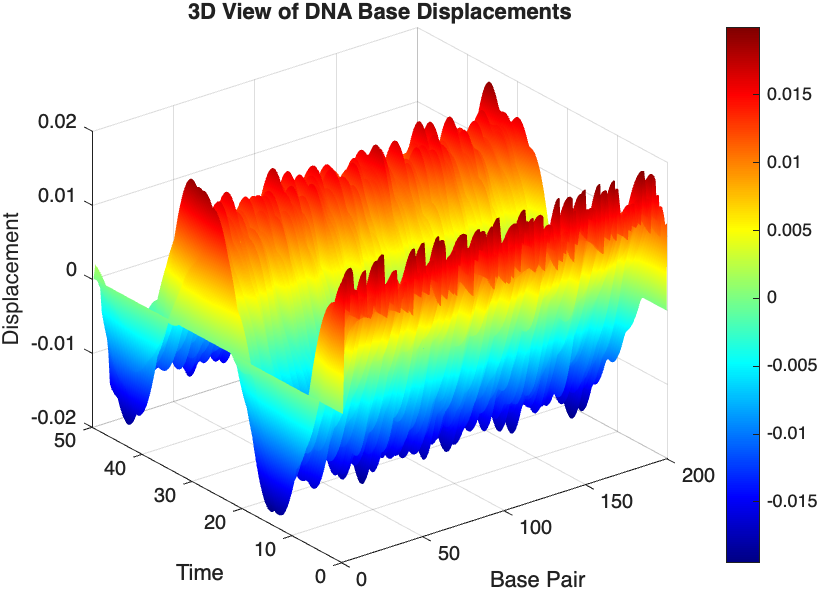
% 3D plot for displacement
figure;
[X, T] = meshgrid(1:numBases, tspan);
surf(X', T', x);
xlabel('Base Pair');
ylabel('Time');
zlabel('Displacement');
title('3D View of DNA Base Displacements');
colormap('jet');
shading interp;
colorbar; % Adds a color bar to indicate displacement magnitude
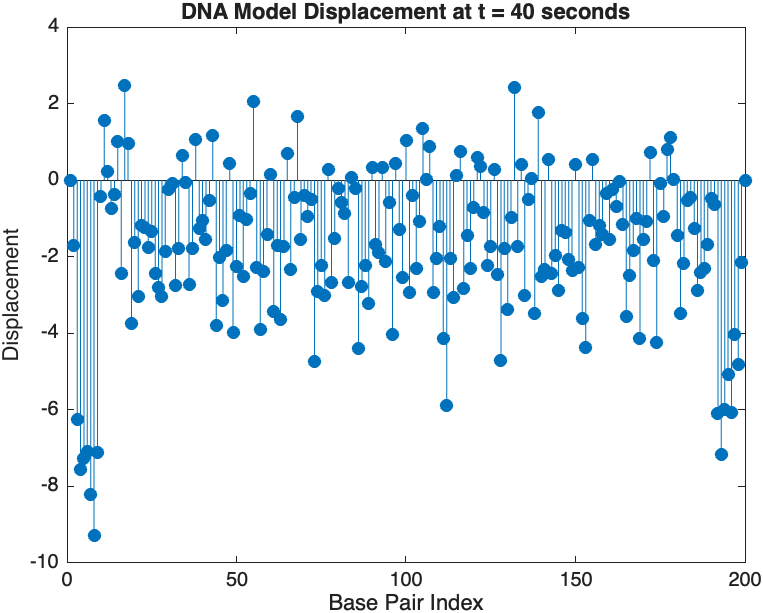
% Snapshot visualization at a specific time
snapshotTime = 40; % Desired time for the snapshot
[~, snapshotIndex] = min(abs(tspan - snapshotTime)); % Find closest index
snapshotSolution = x(:, snapshotIndex); % Extract displacement at the snapshot time
% Plotting the snapshot
figure;
stem(1:numBases, snapshotSolution, 'filled'); % Discrete plot using stem
title(sprintf('DNA Model Displacement at t = %d seconds', snapshotTime));
xlabel('Base Pair Index');
ylabel('Displacement');
% Time vector for detailed sampling
tDetailed = 0:0.5:50; % Detailed time steps
% Initialize an empty array to hold the data
data = [];
% Generate the data for 3D plotting
for i = 1:numBases
% Interpolate to get detailed solution data for each base pair
detailedSolution = interp1(tspan, x(i, :), tDetailed);
% Concatenate the current base pair's data to the main data array
data = [data; repmat(i, length(tDetailed), 1), tDetailed', detailedSolution'];
end
% 3D Plot
figure;
scatter3(data(:,1), data(:,2), data(:,3), 10, data(:,3), 'filled');
xlabel('Base Pair');
ylabel('Time');
zlabel('Displacement');
title('3D Plot of DNA Base Pair Displacements Over Time');
colorbar; % Adds a color bar to indicate displacement magnitude
2
17%
3
12%
4
59%
6
4%
8
5%
Other (comment below)
3%
6419 voti

Welcome to MATLAB Central's first Ask Me Anything (AMA) session! Over the next few weeks, I look forward to addressing any questions or curiosities you might have about MATLAB, the forum, sasquatches, or whatever's on your mind. Having volunteered as a contributor to this community before joining MathWorks, I'm excited to act as a bridge between these two worlds. Let's kick things off by sharing a little-known fact about the forum’s staff contributors!
A couple of years ago, before I joined MathWorks as a developer on the Graphics and Charting team, I often wondered who were the MathWorkers with the [staff] moniker answering questions in the Answers forum. Is their MATLAB Central activity part of their day-to-day job expectations? Do they serve specific roles on some kind of community outreach team? Is their work in the forum voluntary in the same way that non-staff contributors volunteer their time?
Now that I'm on the inside, I'd like to share a secret with my fellow MATLAB users and MATLAB Central enthusiasts: with the exception of the MathWorks Support Team, staff participation in the Answers forum is completely voluntary! The staff contributions you see in the forum arise from pure intrinsic motivation to connect with users, help people out of ruts, and spread the word about our product!
For example, Steven Lord has contributed 20-150 answers per month for 9 years! Steven is a quality engineer for core MATLAB numerical functions. Cris LaPierre develops training material and has been a faithful contributor in the forum for almost 6 years! Kojiro Saito and Akira Agata have been tackling Japanese content for more than 7 years! There are many others who have inspired me as a user, and I am honored to now call colleagues: Peter Perkins, Michio, Joss Knight, Alan Weiss, Jiro Doke, Edric Ellis, and many others who deserve appreciation.
The forum's success hinges on the invaluable contributions from the majority of non-staff volunteers, whose dedication and expertise fuel our community. But I know I wasn't alone in wondering about these staff contributors, so now you're in on the secret!
I'm curious to know what other topics you're interested in learning about. Ask me anything!
numel(v)
6%
length(v)
13%
width(v)
14%
nnz(v)
8%
size(v, 1)
27%
sum(v > 0)
31%
2537 voti
As far as I know, the MATLAB Community (including Matlab Central and Mathworks' official GitHub repository) has always been a vibrant and diverse professional and amateur community of MATLAB users from various fields globally. Being a part of it myself, especially in recent years, I have not only benefited continuously from the community but also tried to give back by helping other users in need.
I am a senior MATLAB user from Shenzhen, China, and I have a deep passion for MATLAB, applying it in various scenarios. Due to the less than ideal job market in my current social environment, I am hoping to find a position for remote support work within the Matlab Community. I wonder if this is realistic. For instance, Mathworks has been open-sourcing many repositories in recent years, especially in the field of deep learning with typical applications across industries. I am eager to use the latest MATLAB features to implement state-of-the-art algorithms. Additionally, I occasionally contribute through GitHub issues and pull requests.
In conclusion, I am looking forward to the opportunity to formally join the Matlab Community in a remote support role, dedicating more energy to giving back to the community and making the world a better place! (If a Mathworks employer can contact me, all the better~)
We're thrilled to unveil a new feature in the MATLAB Central community: User Following.
Our community is so lucky to have many experienced MATLAB experts who generously share their knowledge and insights across different applications, including Answers, File Exchange, Discussions, Contests, or Blogs.
With the introduction of User Following feature, you can now easily track new content across different areas and engage in discussions with people you follow. Simply click the ‘Follow’ button located on their profile page to start.
Depending on your communication setting, you will receive notifications via email and/or view updates in your ‘Followed Activity’ feeds. To tailor your feed, select the ‘People’ filter and focus on activities from those you follow.
We strongly encourage you to take advantage of the User Following feature to foster learning and collaboration within our vibrant community.
Who will be the first person you choose to follow? Share your answer in the comments section below and let's inspire each other to explore new horizons together.
ismissing( { [ ] } )
26%
ismissing( NaN )
18%
ismissing( NaT )
11%
ismissing( missing )
21%
ismissing( categorical(missing) )
9%
ismissing( { '' } ) % 2 apostrophes
16%
896 voti
What's your way?

I created an ellipse visualizer in #MATLAB using App Designer! To read more about it, and how it ties to the recent total solar eclipse, check out my latest blog post:
Github Repo of the app (you can open it on MATLAB Online!):
Mari is helping Dad work.

Today, he got dressed for work to design some new dog toy-making algorithms. #nationalpetday

Transforming my furry friend into a grayscale masterpiece with MATLAB! 🐾 #MATLABPetsDay ✌️
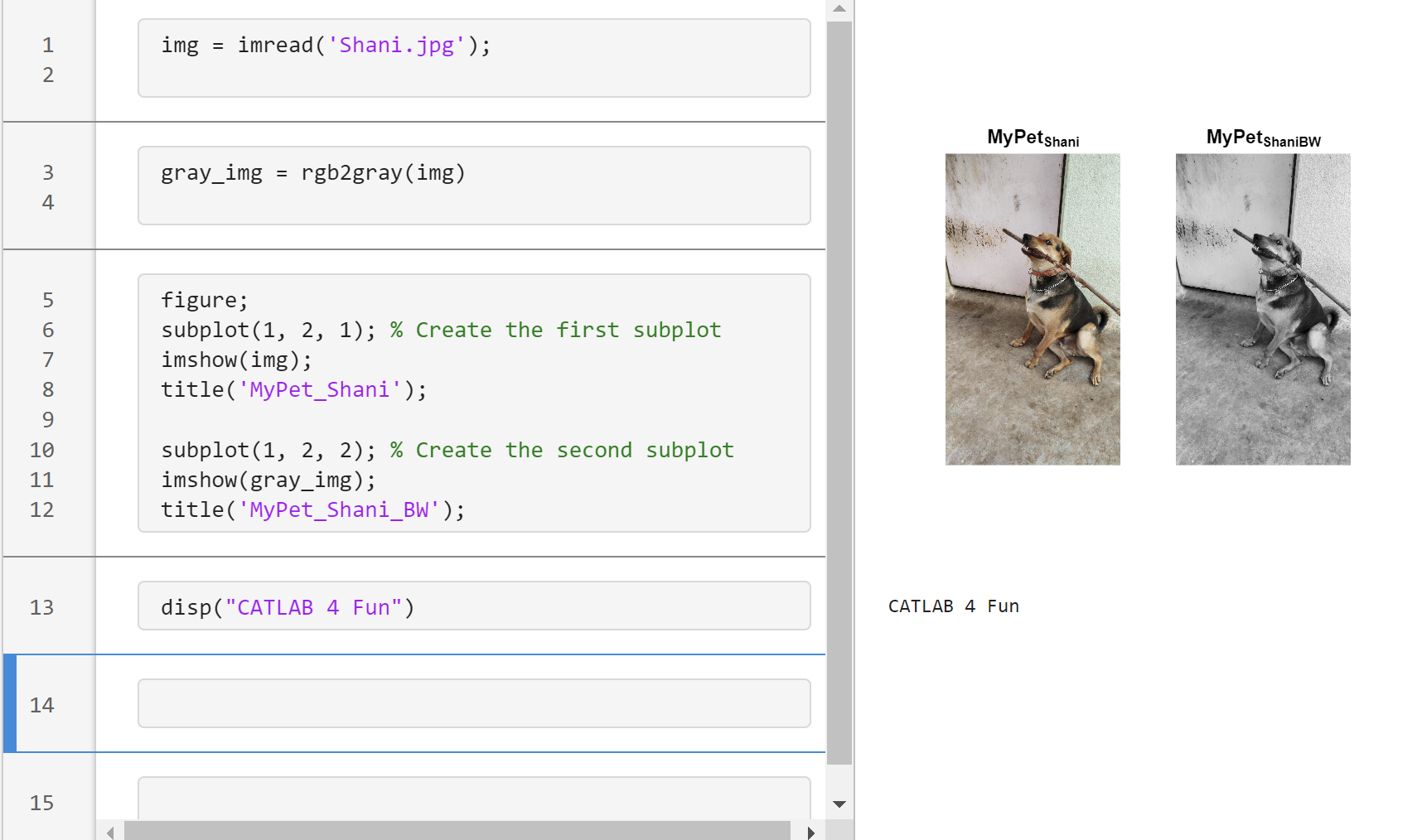

This is Stella while waiting to see if the code works...

Hey MATLAB Community! 🌟
As we continue to explore, learn, and innovate together, it's essential to take a moment to recognize the remarkable contributions that have sparked engaging discussions, solved perplexing problems, and shared insightful knowledge in the past two weeks. Let's dive into the highlights that have made our community even more vibrant and resourceful.
Interesting Questions
Burhan Burak brings up an intriguing issue faced when running certain code in MATLAB, seeking advice on how to refactor the code to eliminate a warning message. It's a great example of the practical challenges we often encounter
Jenni asks for guidance on improving linear models to fit data points more accurately. This question highlights the common hurdles in data analysis and model fitting, sparking a conversation on best practices and methodologies.
Popular Discussions
A thought-provoking question posed by goc3 that delves into the intricacies of MATLAB's logical operations. It's a great discussion starter that tests and expands our understanding of MATLAB's behavior.
Toshiaki Takeuchi shares an insightful visualization of the demand for MATLAB jobs across different regions, based on data from LinkedIn. This post not only provides a snapshot of the job market but also encourages members to discuss trends in MATLAB's use in the industry.
From the Blogs
Mike Croucher shares his excitement and insights on two long-awaited features finally making their way into MATLAB R2024a. His post reflects the passion and persistence of our community members in enhancing MATLAB's functionality.
In this informative post, Sivylla Paraskevopoulou offers practical tips for speeding up the training of deep learning models. It's a must-read for anyone looking to optimize their deep learning workflows.
A Heartfelt Thank You 🙏
To everyone who asked a question, started a discussion, or wrote a blog post: Thank you! Your contributions are what make our community a fountain of knowledge, inspiration, and innovation. Let's keep the momentum going and continue to support each other in our journey to explore the vast universe of MATLAB.
Happy Coding!
Note: If you haven't yet, make sure to check out these highlights and add your voice to our growing community. Your insights and experiences are what make us stronger.
You reached this milestone by providing valuable contribution to the community since you started answering questions in Since September 2011.
You were very active in the first year, and took some break, but you steadily rose ranks in the recent years to achieve this milestone.
You provided 3954 answers and received 1503 votes. You are ranked #25 in the community. Thank you for your contribution to the community and please keep up the good track record!
MATLAB Central Team
In honor of National Pet Day on April 11th, we're excited to announce a fun contest that combines two of our favorite things: our beloved pets and our passion for MATLAB/Simulink! Whether you're a cat enthusiast, a dog lover, or a companion to any other pet, we invite you to join in the fun and showcase your creativity.
How to Participate:
- Take a photo of your pet featuring any element of MATLAB/Simulink.
- Post it in the Fun channel of the Discussions area.
- Include a brief description or story behind the photo - we love to hear about your pets and your creative process!
🏆 Prizes:
We will be selecting 3 winners for this contest, and each winner will receive a MathWorks T-shirt or hat! Winners will be chosen based on creativity, originality, and how well they incorporate the MATLAB/Simulink element into their photo.
📅Important Dates:
Contest ends on April 12th, 2024, at 11:59:59 pm, Eastern Time
We can't wait to see all of your adorable and creative pet photos. Let's celebrate National Pet Day in true MathWorks style. Good luck, and most importantly, have fun!

I'm excited to share some valuable resources that I've found to be incredibly helpful for anyone looking to enhance their MATLAB skills. Whether you're just starting out, studying as a student, or are a seasoned professional, these guides and books offer a wealth of information to aid in your learning journey.
These materials are freely available and can be a great addition to your learning resources. They cover a wide range of topics and are designed to help users at all levels to improve their proficiency in MATLAB.
Happy learning and I hope you find these resources as useful as I have!
I found this link posted on Reddit.
https://workhunty.com/job-blog/where-is-the-best-place-to-be-a-programmer/Matlab/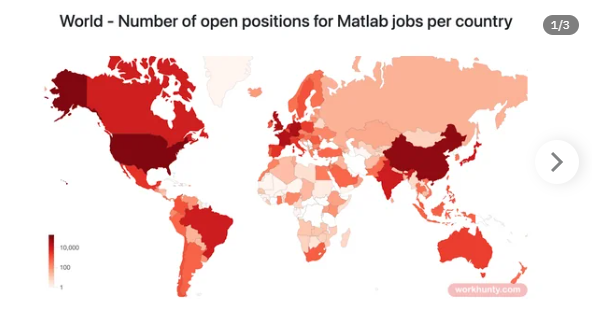

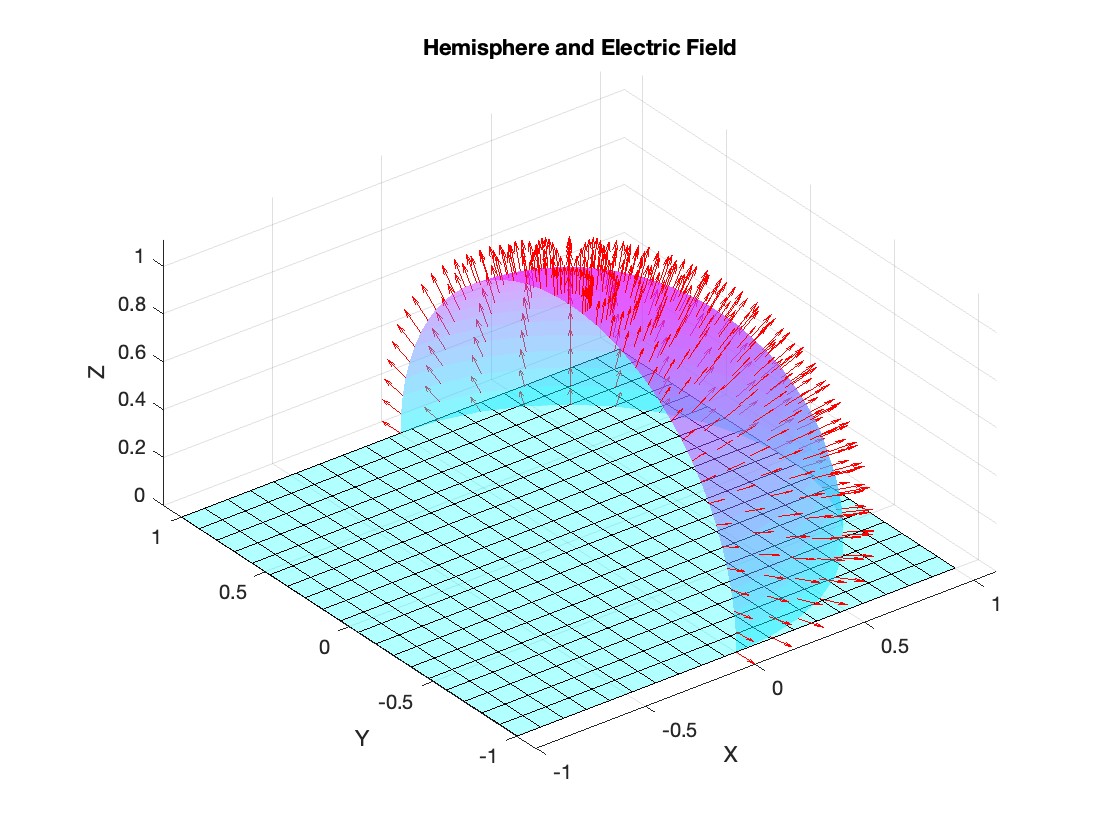
Let S be the closed surface composed of the hemisphere 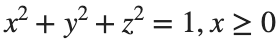 and the base
and the base  Let
Let 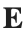 be the electric field defined by
be the electric field defined by  . Find the electric flux through S. (Hint: Divide S into two parts and calculate
. Find the electric flux through S. (Hint: Divide S into two parts and calculate 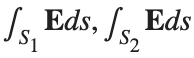 ).
).
% Define the limits of integration for the hemisphere S1
theta_lim = [-pi/2, pi/2];
phi_lim = [0, pi/2];
% Perform the double integration over the spherical surface of the hemisphere S1
% Define the electric flux function for the hemisphere S1
flux_function_S1 = @(theta, phi) 2 * sin(phi);
electric_flux_S1 = integral2(flux_function_S1, theta_lim(1), theta_lim(2), phi_lim(1), phi_lim(2));
% For the base of the hemisphere S2, the electric flux is 0 since the electric
% field has no z-component at the base
electric_flux_S2 = 0;
% Calculate the total electric flux through the closed surface S
total_electric_flux = electric_flux_S1 + electric_flux_S2;
% Display the flux calculations
disp(['Electric flux through the hemisphere S1: ', num2str(electric_flux_S1)]);
disp(['Electric flux through the base of the hemisphere S2: ', num2str(electric_flux_S2)]);
disp(['Total electric flux through the closed surface S: ', num2str(total_electric_flux)]);
% Parameters for the plot
radius = 1; % Radius of the hemisphere
% Create a meshgrid for theta and phi for the plot
[theta, phi] = meshgrid(linspace(theta_lim(1), theta_lim(2), 20), linspace(phi_lim(1), phi_lim(2), 20));
% Calculate Cartesian coordinates for the points on the hemisphere
x = radius * sin(phi) .* cos(theta);
y = radius * sin(phi) .* sin(theta);
z = radius * cos(phi);
% Define the electric field components
Ex = 2 * x;
Ey = 2 * y;
Ez = 2 * z;
% Plot the hemisphere
figure;
surf(x, y, z, 'FaceAlpha', 0.5, 'EdgeColor', 'none');
hold on;
% Plot the electric field vectors
quiver3(x, y, z, Ex, Ey, Ez, 'r');
% Plot the base of the hemisphere
[x_base, y_base] = meshgrid(linspace(-radius, radius, 20), linspace(-radius, radius, 20));
z_base = zeros(size(x_base));
surf(x_base, y_base, z_base, 'FaceColor', 'cyan', 'FaceAlpha', 0.3);
% Additional plot settings
colormap('cool');
axis equal;
grid on;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Hemisphere and Electric Field');
isempty( [ ] )
10%
isempty( { } )
13%
isempty( '' ) % 2 single quotes
13%
isempty( "" ) % 2 double quotes
24%
c = categorical( [ ] ); isempty(c)
18%
s = struct("a", [ ] ); isempty(s.a)
22%
1324 voti
