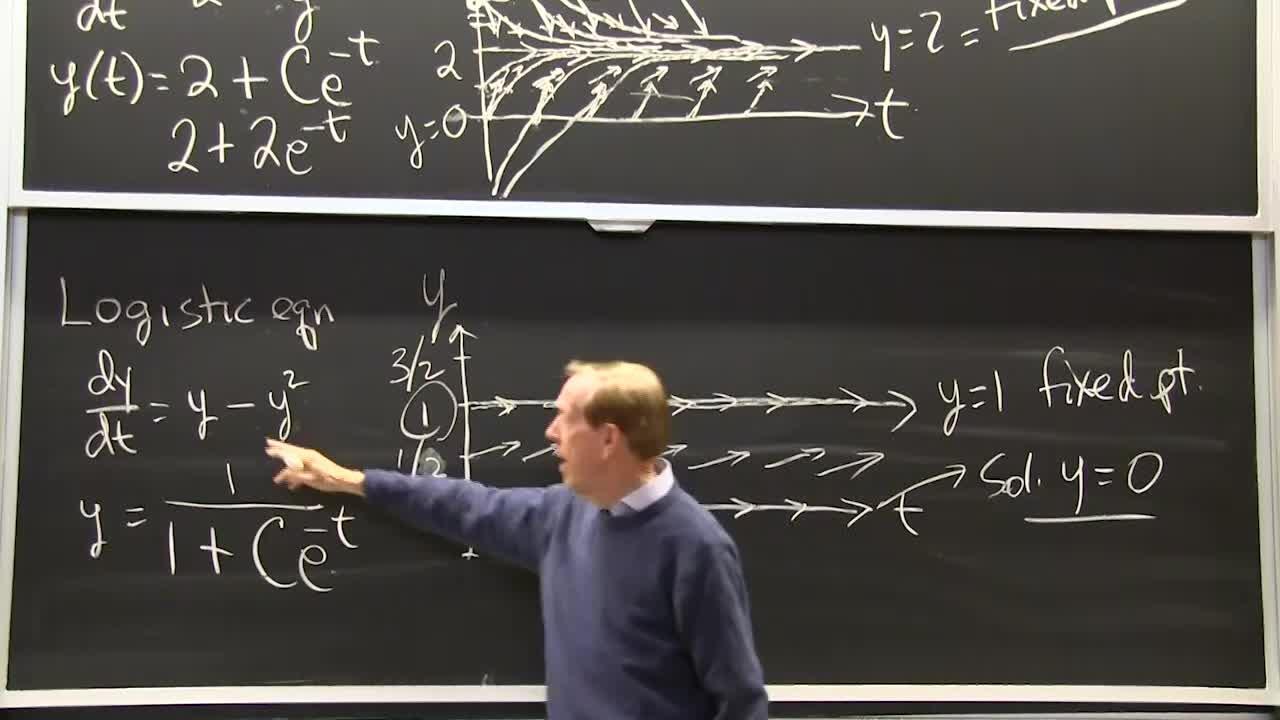Differential Equations and Linear Algebra, 3.1: Pictures of the Solutions
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
The direction field for dy/dt = f(t,y) has an arrow with slope f at each point t, y. Arrows with the same slope lie along an isocline.
Published: 27 Jan 2016
OK. So we've moved on into Chapter 3. Chapter 1 and 2 were about equations we could solve, first order equations, chapter one; second order equations in chapter 2, often linear, constant coefficient sometimes. Now we take any equation. And I'll start with first order.
First derivative is some function and not a linear function, so I don't expect a formula. A solution will exist. But I won't have a formula for the solution. But I can make a picture of the solution. You see what's happening as time goes on. And so that's today's lecture, is a picture.
So this function, whatever it is, gives the slope of y. That's the slope. And it will be the slope of the arrows that I will draw in this picture. So here's a picture that started, y, t. And the slope of the arrows is f. And here is my example. Well, you will see. I chose a constant coefficient linear equation. Because I could find a solution. So 2 minus y, I know from that minus sign that I'm going to have exponential decay in the null solution. And then y equal to 2 is a very special particular solution, a constant.
And in my picture, y equal to 2, it jumps out. Because when y is 2, when y is 2 the slope is 0. So all my arrows on the y equal to 2 line, have slope 0. So that's a very special line. And since the solution follows the arrows that's the whole point. The solution follows the arrows. Because the arrows tell the slope.
So if I'm on that line, the solution just follows those arrows, and stays on the line. y equal to 2 is a fixed point, fixed point of the solution, a fixed point for the equation. And the question is, if I don't start at y equal to 2, do I move toward 2 or away from it? OK.
So I can see from the formula what the answer is going to be. If I start with some other value, some other value of c not 0, then there will be a null solution part. But as t gets large that goes to 0. So I move toward 2. Now let's see that in the picture.
So let me-- I'm drawing the arrows first. So this is all time starting at if y is 0, then if y is 0 then dy dt is 2. So I draw arrows with slope 2, along the y equals 0 line. This is the y equals 0 line. All my arrows have slope 2.
Now what else? So that's a few arrows that show what will-- so the solution if it starts there, will start in the direction of that arrow. But then I have to see what the other arrows are for other values of y. Because right away the solution y will change. And the slope will change. And that's it needs more arrows. Well, actually it needs way more arrows than I can possibly draw.
Let me draw another line of arrows when y is 1, along that line, along the line y equal 1. When y is 1, 2 minus 1 is 1. The slope is 1. f is 1. And my arrows have slope 1. So all along here, the arrows go up. Those went up steeply with slope 2. Now the arrows will go up. So I'll have arrows that are going a 45-degree angle, slope 1.
Do you see? I hope you begin to see the picture here. The solution might start there. It would start with that slope. But it will curve down. Because the arrows are not so steep. As I go upward, the arrows are getting flat. And so the curve that follows the arrows has to flatten out, flatten out, flatten out. The arrows are still, at that point the arrows are still slope 1. But it's flattening out. And it's never going to cross this line. And it will run closer and closer to that line. And wherever it starts, if it starts at time t equals to 1 there, it'll do the same thing. And it will stay just below the other one.
Do you see what the pictures are looking like? If it starts at different times, so these are different times. These are different starts. Yeah, really we're used to, at t equals 0, we're used to giving y of 0. So this is starting at 0. This is starting at 2. Starting at 1 would be a higher start. What about starting at 4?
Suppose y of 0 is 4. That point is t equals 0, y equal 4. So that point is y of 0 equal 4. What's the graph of the solution with that start? Actually, I could figure out what the solution would be if y of 0 was 4, I'd have 2 plus 2 e to the minus t. At t equals 0, that's 4. And it fits. It solves the equation. And it's going to be its graph. I should be able learn that from the arrows.
So along this line of y equal 4, all the arrows when y is 4, the slope is minus 2. So these arrows from these points, go down with slope minus 2. But the solution starts down. So it starts like that. But then it has to follow the new arrows. And the new arrows are not so steep. So the new arrows are I have slope minus 1. I hope my picture is showing the steeper slope 2 along this line, and the flatter slope 1, or rather minus 1 downwards, along this line. So it just follows along here.
Well of course it's just a mirror image of that one. It's a mirror image of that one. I'm trying to show the graph of all solutions from all starts, the whole plane. Actually I could go, t could go to minus infinity. And y could go all the way from minus infinity up, all the way up. I could fill the whole board here with arrows, and then with solutions. And the solutions would follow the arrows, the arrows changing slope and actually in this case, all solutions wherever you started, would approach 2.
And that's what the formula says. But we get that information from the arrows with no formula. Let me show you a next example. And here's our next example. The logistic equation, it's not linear. So it's going to be more interesting.
And do you remember the solution? You remember maybe the trick with the logistic equation was 1 over the solution, gave a linear equation and expression like that. OK. Time to draw arrows.
OK. When y is 0-- so here's y-- when y is 0, the slope is 0. So I have a whole line of flat. I have a flat horizontal line. That's the solution, y equals 0 fixed point. Also we have another fixed point. When y is 1, 1 minus 1 is 0. Slope is 0. Slope stays 0. The arrows all have zero slope along the line y equal 1. So there is another solution, which doesn't do anything exciting. It just stays at 1. y equal 1 is another fixed point, steady state, whatever words we want to use.
But again, the real picture is what about other starts. What about a start at 1/2? Well if it starts at-- if y is 1/2 half at the starting time, what is the slope? 1/2 minus 1/4 is 1/4. So the slope is upwards, but not very steep. The slope along the-- and it doesn't depend on t in these examples. So that slope is the same as long as y is 1/2, doesn't matter what the time is. y equals 1/2 gives me a 1/2 minus 1/4, which is a 1/4. It gives me that slope.
What about the slope 1/4? So 1/4, I have 1/4 minus 1/16. I think that's 3/16. So it's beginning to climb upward. So it's upwards again. But 3/16 is a little-- I don't know if I'm going to get the picture too brilliantly. The slope, as soon it-- if it just starts a little above 0, what happens to the solution that starts a little bit above 0?
It climbs. Because if y is above 0, say if it starts between 0 and 1, if y is between 0 and 1, then y is bigger than y squared. And the slope is positive. And it goes up. So do you see what it's doing? The slope will just, if it starts a little bit above, it'll have a small slope. But that slope will gradually increase. But then actually at this point, the slope is 3/4 minus whatever it is. It slows down, still going upwards. y is still bigger than y squared.
You recognize what the curve is going to look like. So there is an S curve. It's an S curve. Which we saw for the logistic equation, and here we have a formula for it. Well, the whole point of today's video was we don't need a formula. So you don't need that. The arrows will tell you that it starts up slowly. It gets only-- that's the biggest slope it gets. And then it starts down. The slope goes down again. But it's still a positive slope. Still climbing, climbing, climbing, and approaching 1.
Now that's sort of a sandwich in the picture. But it could start with a negative. So what happens if it starts at y equal minus 1? The slope, if y is minus 1, we have minus 1, minus 1, a slope of minus 2. That's a steeper serious downward slope. So the solution that starts here has-- that's tangent. You see that it's tangent to the arrow, because it has the same slope as the arrow. And it comes down. But as it goes down, the slopes are getting steeper. Whoops, not flatter, but steeper.
For example, if y is minus 2, I have minus 2, minus 4 is minus 6. So as soon as it gets down to minus 2, the slope has jumped way down to minus 6. So here is the-- it falls right off. It's a drop-off curve, a drop-off curve. It falls right off actually to infinity. It never makes it out to-- it falls down to y equal minus infinity in a fixed time, in a definite time.
And so here's a whole region of curves going down to minus infinity. Here is a whole region. What happens in this region? Suppose y starts at plus 2? Well, I have 2 minus 4. So the slope is negative. The slope is negative up here. Yeah. And this is the big picture. The slope, the arrows are positive below this line. They're upward. They were downward here. They're slowly upward in this sandwich. And then up above, they're downward again.
So if slopes are coming down, and they drop into actually it's a symmetric picture. Really-- no reason not to go backwards in time. Where are these coming from? They're all coming from curves. The whole plane is full of curves. And these start at plus infinity. They drop into 2. These start below 0, and they drop off to minus infinity. And then the real interest in studying population was these.
Can you do one more example? Let me take a third example that has a t in the function. So the arrows won't be the same along the whole line. In fact, the arrows will be the same. So if I have 1 plus t minus y, that's the f, equal a constant. Then that's a curve-- well, it's actually a straight line. It's actually a 45-degree line in this plane. And along that line the f, this is the f, the f of t and y, the arrow slope. The arrows slopes are the same along that line. That line is called an isocline. This is called an I-S-O, meaning the same, cline, meaning slope. So that's an isocline.
Here's an isocline. It's a 45-degree line. That's the 45-degree line, 1 plus t minus y equal 1. Let me draw the 45-degree line 1 plus t minus y equals 0. So it's a little bit higher. OK. Now arrows, and then put in the curves, the solution curves that match the arrows.
So the arrows have this slope along that line. Along this line, 1 plus t minus y, they have slope 0. Oh, interesting. At every point on the line the slope is 0. Because this is the slope of the arrows. At every point on this line, the slope is 1, also very interesting. Because that's right along the line.
So here we have a solution line. That must be a solution line. That's the line where y is t. That's a very big 45-degree important line. Because if y equals t, if y equals t then dy dt should be 1. And it is 1 for y equals t. So that's a solution line with that solution.
Now what about a line with 1 plus t minus y equal minus 1, a line? If 1 plus t minus y is minus 1, if f is minus 1, the slope is negative. So what does that mean? If 1 plus t minus y is minus 1, the slope is negative. So at points on this line, the slope is going downwards. Oh, interesting. I wasn't quite expecting that. Let me just see if I got a suitable picture. Why is it not right?
If 1 plus t minus y is-- oh, I'm sorry. This is the line, y equal 1 plus t. I think what I'm expecting to see is I'm expecting to see it from the formula too that as time goes on, this part goes to 0, and y goes to t. I believe that all the solutions will approach this y equal to t. I think their slopes, their slopes here-- darn, that's not right. Their slopes should be coming upwards. Yeah, let me-- I can figure that out.
If t is let's say 1, and y is 0. OK. If t is 1, and y is 0, I have a slope of 2. Good. OK. There's a point t equal to 1. Here is 0, 0. Here's the point t equal to 1, y equals 0. The slope came out to be 2. It went up that way. So along that line, the slopes are going up. Along this line, the slopes are right on the line. On this line the slopes are flat, and the curve is moving toward the line.
I'll just draw the beautiful picture now of the solution. So the solutions look like this. They are-- this is the big line. You've got to keep your eye on that line. Because that's the steady state line that all solutions are approaching. So if you have the idea of arrows to show the slope, fitting solution curves through tangent to the arrows, and sometimes having a formula to confirm that you did it right, you get a picture like this. So that's the idea of first order equations, which are graphed in the y-t plane. And the arrows tell you the derivative. Thanks.