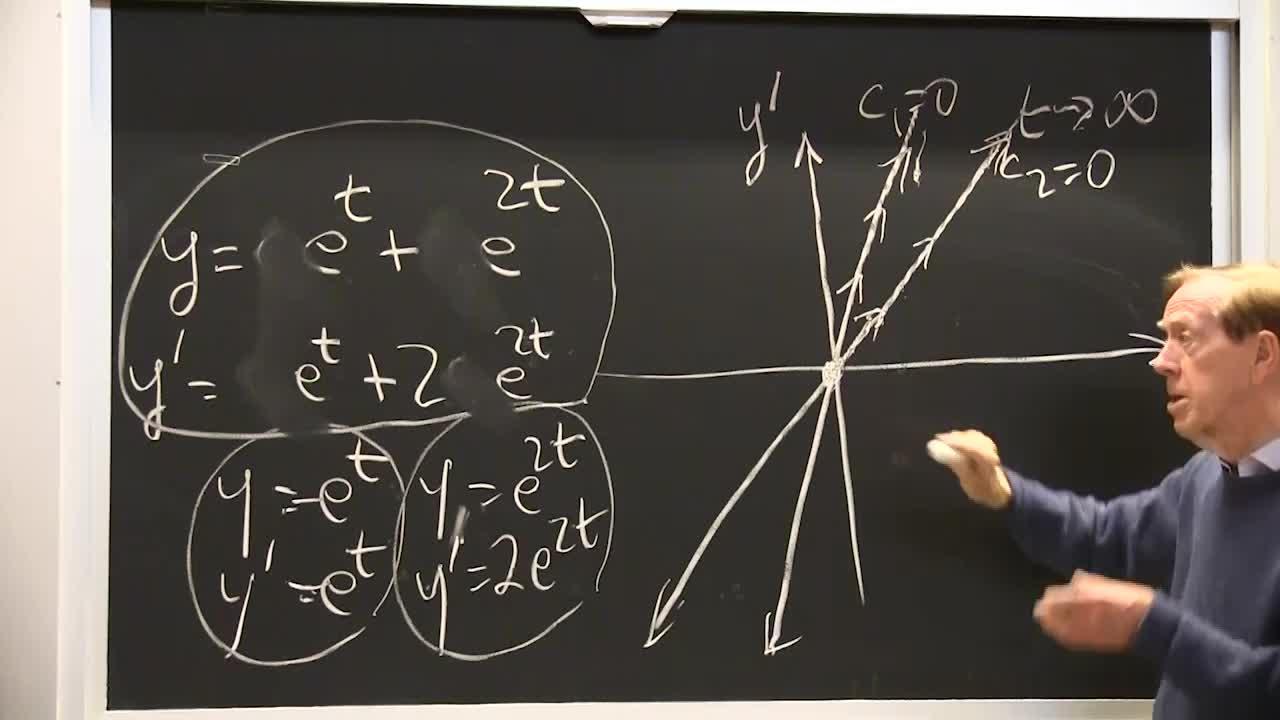Differential Equations and Linear Algebra, 3.2: Phase Plane Pictures: Source, Sink Saddle
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
Solutions to second order equations can approach infinity or zero. Saddle points contain a positive and also a negative exponent or eigenvalue.
Published: 27 Jan 2016
OK. This is the second video for Chapter 3. And it's going to be pictures again. But it's pictures for a second order equation. And I'll make them-- these will be nice. We'll know formulas here. These will be constant coefficient, linear second order equations. And we know that the solution-- there are two special solutions, e to the s1 t and e to the s2t, two null solutions, and any combination is a null solution. So we're talking about null equations, 0 on the right-hand side. And we just want to draw that picture that goes with solutions like that.
So here is the magic word, phase plane, phase plane. We're going to draw the pictures in a plane. Because that's what a blackboard is. And the axes we'll choose will be y and y prime, not t. You'll see how t, time, comes into the picture. But we have the two axes will be y and y prime.
So I had to figure out what y prime was. It just brings down an s1 from that term, and brings down an s2 from that term. And now here's the example. Here is the first example.
So I took this particular equation. Notice that the damping term is negative. I have negative damping. This will be unstable. Solutions will go out to infinity. And I can find those solutions. Because you know that I look for e to the st. I always look for e to the st. I plug in e to the st. I get an s squared from two derivatives, minus 3s from one derivative, plus 2 equaling 0. I factor that, and I find the 2s1 is 1, and s2 is 2. And now I'm ready for the phase plane picture.
OK. Phase plane picture, so here are my solutions. s is 1 or 2. Then the derivative has a 1 or a 2. And here's my plane. Here's my plane. And I want to draw on that the solutions. These solutions, I actually have formulas. I just want to draw them. So I'm plotting.
One example would be that c1 be 1, and let c2 be 0. So that's gone. c1 is 1. I just have that picture. What kind of a picture do I have in the phase plane, in the y, y prime plane, when that's y and that's y prime? Well, those are equal.
So y equals y prime for that solution. y equals y prime along the 45-degree line. It's just like y equal x. y prime is y. And what's happening on this 45-degree line? The solution is this solution, is going straight out the line. As t increases, y and y prime both increase. I go out. This is t going to infinity.
And what about t going to minus infinity? Because we got the whole picture here. When t goes to minus infinity that goes to 0, that goes to 0. Here is the point where the universe began. The Big Bang is right there at t equal minus infinity. And as t increases, this point, y, y prime, is traveling along that 45-degree line. Because y equals y prime, and out there.
And what about the rest of the line? Well, if c1 was negative, if c1 was negative I'd have a minus there, and a minus there. I would just have minuses. And I'd be going out that line. Well, that's one line in my whole plane, but not all.
Now let me take as a second line c1 equals 0. So nothing from e to the t, and let me take y as e to the 2t, and y prime then would be 2e to the 2t. OK. What's happening in the phase plane for this solution, now looking at this one?
Well in this solution, in this case, y prime is 2 times y. y prime is 2 times y. So I'm staying on the line y prime, where y prime is 2 times y. It's a steeper line, steeper line. So that was the case, this was the line where c2 was 0. There was no e to the 2t on that first line that we drew. In the second line that we drew, c1 is 0. There's no e to the t. Everything is in e to the 2t.
So now c1 is 0 on this line. OK. And we just go out it. As t increases, y prime increases faster. Because of the factor 2. So it goes up steeply. And it goes this way. When c2 is negative, if I took a minus and a minus, I would just go down the other way on the same line. And this is still the Big Bang, t equal minus infinity, where everything starts. OK.
So that is two lines, the two special lines in the phase plane. But now I have to draw all the other curves. And they will be curves. And where will they come from? They will come from a combination. So now I'm ready for that one.
Let me take the case c1 equal 1, c2 equal 1. Yeah, why not? c1 equal 1. So I can erase c1. c2 equal 1, I can erase c2. And now I have another solution, y and y prime. And I want to put it in the phase plane. So at every value of t, at every value of t that's a point. That's a value of y. This is a value of y prime. I plot the points y and y prime, and I look at the picture.
And again as t changes, as t changes I'll travel along the solution curve in the phase plane. I'll travel along. As t changes, y will grow, y prime will grow. I'll head out here. But I won't be on that straight line or that straight line. Because those were the cases when I had only one of the two solutions. These were the special solutions. And now I have a combination.
So what happens as t goes to infinity? As t goes to infinity, this wins. As t goes to infinity, the e to the 2t is bigger than e to the t. So this is the larger term. So it approaches. This curve now will approach closer and closer to the one when the line with slope 2. The 2 will be the winner out here.
But at t equal minus infinity, near the Big Bang, at t equal minus infinity, e to the 2t is even more small. So at t equal minus infinity, or t equal minus 10, let's say, this is e to the minus 10. This would be e to the minus 20; very, very, very small. These would win.
So what happens for this solution is it starts out along the line given by the not-so-small t, the not-so-small exponent. It starts up that line. But t is increasing. When t passes some point, this 2t will be bigger than t. And it will, I guess, at t equals 0, 2t will be bigger than t. And from that point on, from the t equal 0 point-- oh, I could even plot the t equals 0.
So at t equals 0, y is 2 and y prime is 3. So at 1, 2, 1, 2, 3; somewhere in there. So you see, the curve starts up along the line where e to the t is bigger. They have the same size at t equals 0, both equal 1. This is at t equals 0. And then for large times, this one wins. So I approach that line.
I don't know if you can see that curve. And I don't swear to the slopes of that curve. But in between in there is filled with curves that start out with this slope, and end with that slope. And the same here, it'll start with this slope. But then go-- probably this is a better picture. Yeah. That's a better picture. Yeah. It will just go up with slope. At the end it will have slope 2 going upwards. Yeah. That looks good.
Well, you could say I only drew part of the phase plane. And you're completely right. If I start somewhere here, what would you think would happen? What would you think would happen if I start with that value of y that much, and that value of y prime? It would have some mixture of-- there would be a c1 and a c2. So the other curves that I haven't drawn yet come from the other c1 and c2.
I've done c1 equal 1, and c2 equal 1. And c1 equal c2 equal 1. But now I have many more possibilities. And what they do is they will-- so suppose I start there. It will approach-- this is the winner. This is the winner. Where c1 is 1, where this is happening, there is the winner for large time.
So all curves swing up toward parallel to that line. Or down here, they swing down parallel to that line. So things here will swing down this way. That's the phase plane.
May I do one more example to show that this was a source? This is called a source. Because the solution goes to infinity. Wherever you start, the solution goes to infinity. It's unstable, totally unstable.
Now if I change to a positive damping, then I would have a plus sign there. These would be plus signs. I would have s equal minus 1, or s equal minus 2. So with positive damping, I damp out naturally. And this picture would be the same, except all the lines are coming in to 0, 0. The solutions are damping to 0, 0; to nothing happening. So I just track the same lines, but in the opposite direction. So instead of this being the Big Bang, it's the end of the universe, t equal infinity.
OK. I'm up for one more picture of this possibility. And let me take the equation y double prime equal 4y. So my equation will be s squared equal 4, s equals 2 or minus 2. And when I draw the phase plane and the solutions, the solutions will be c1 e to the 2t, and c2 e to the minus 2t, from a 2 and a minus 2. That's the solution we all know.
And now I should compute its slope. y prime will be 2c1 e to the 2t minus 2c2 e to the 2t. And now you just want me to draw those pictures. You just want me to draw those pictures, and let me try to say what happens here.
This is a saddle point. It's called a saddle, when we have in one direction things are growing, but in the other, things are decreasing. So most solutions, if c1 is not 0, then the growth is going to win, and that will disappear. But there is the possibility that c1 is 0. So there will be one line coming from there. There will be one line coming from there. Maybe I can try to draw that.
Again, I'll draw that pure line, where c1 is 0. So that pure line is coming. These are minuses here. So that line is coming in to the center. So that's why we have a saddle. We approach a saddle if along this where this is minus 2 of that, so I think it would be-- so it's a slope of minus 2. So I think a slope like that, so again this is y. This is y prime. This is the slope of minus 2. And that's this curve.
So it will be very exceptional that we're right on that line. All other points, all other curves in this phase plane, are going to have a little c1 in them. And then this will take over. And that gives us, as we saw before, this slope. This is 2 times that. So that line is where everybody wants to go. And only if you start exactly on this line do you get this picture, and you come into the saddle.
Instead of the Big Bang, or the end of the universe, this is now the saddle point, where we come in on this most special of all lines, coming from this picture. But almost always this is the dominant thing. And we go out.
So if I take a typical starting point, I'll go out this like that, or like this, oh no. Yeah, no. I'll go out. It'll have to go out. So if I start anywhere here, these are probably they're hyperbolas going out in that direction. I don't swear that they're hyperbolas.
Here again we might start in. Because we have big numbers here. But then e to the t takes over. And we go out. So those go out. These go out. And these go out. So this is the big line. That's the line coming from here. And that's where everything wants to go, and everything eventually goes that way, except the one line where c1 is 0.
So this dominant term is not even here then. And then we should become inwards. So that saddle point is the special point where you could go out, if you go the right way. Or you could come in, if you go the other special, special way.
OK. So that sources, sinks and saddles. And I still have to draw the pictures, which involves spirals that come from complex s, where we have oscillation. That'll be the next video.