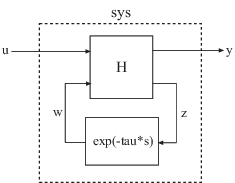
getDelayModel
State-space representation of internal delays
Description
[ returns the set of state-space matrices
and internal delay vector that explicitly describe the state-space model
A,B1,B2,C1,C2,D11,D12,D21,D22,E,tau]
= getDelayModel(sys)sys.
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2006a