LPV Model of Magnetic Levitation System
This example uses an analytic linear parameter-varying (LPV) model of a magnetic levitation system to control the height of a ball. In this example, you build the LPV plant model directly from the linearized equations of motion.
Nonlinear System
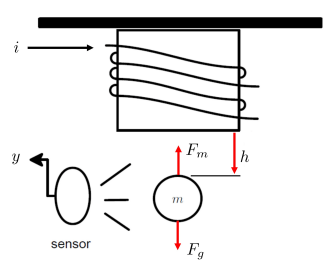
This figure shows the magnetic ball levitation device and its key components. A current (A) is supplied to a coil, which creates a magnetic force on the ball. The position of the ball is denoted by (m). An infrared sensor measures the position of the ball (V). The objective is to make the ball levitate at a desired position . There are two key forces on the ball: the gravity pull and magnetic force .
This nonlinear equation defines the dynamics of the model.
Here:
is the mass of the ball (kg).
is the gravitational acceleration (m/s^2).
is the magnetic force constant (Nm/(A^2)).
Define the model parameters.
mb = 0.02; g = 9.81; alpha = 2.4832e-5;
Equilibrium Conditions
An equilibrium (steady-state) condition with ball height is characterized by the equation
.
The required current to maintain this height is
.
Linearized Equations of Motion
To build an LPV approximation of this plant, choose as scheduling variable and linearize the equations of motion around the -dependent equilibrium conditions
.
This yields the LPV model
with
and
.
The matrices and offsets of this system are defined in the function dataFcnMaglev.m.
Use lpvss to create the model.
Glpv = lpvss('h',@dataFcnMaglev);Gain-Scheduled PID Controller
For PID tuning, pick a few values of and sample the LPV dynamics at these heights to obtain local LTI models.
Pick three height values between 0.05 and 0.25.
hmin = 0.05; hmax = 0.25; hcd = linspace(hmin,hmax,3); [Ga,Goffsets] = sample(Glpv,[],hcd); size(Ga)
1x3 array of state-space models. Each model has 1 outputs, 1 inputs, and 2 states.
Use pidtune to tune a PID controller for each value of . The target crossover frequency is set to 50 rad/s.
wc = 50;
Ka = pidtune(Ga,'pid',wc);
Ka.Tf = 0.001;Now use ssInterpolant to construct a gain-scheduled PID controller that linearly interpolates the tuned gains between the selected values of . This controller also uses the trim current as feedforward control so that the PID regulates the current around its equilibrium value.
Ka.SamplingGrid.h = hcd;
Koffsets = struct('y',{Goffsets.u});
Klpv = ssInterpolant(ss(Ka),Koffsets);LTI Analysis
For evaluation purpose, model the ideal response as a second-order systems Tideal.
wn = 30; zeta = 0.7; Tideal = tf(wn^2,[1 2*zeta*wn wn^2]);
Sample the closed-loop LPV dynamics over a finer grid.
hs = linspace(hmin,hmax,5);
Simulate the step response of the closed-loop model and compare with Tideal.
Tlpv = feedback(Glpv*Klpv,1); step(sample(Tlpv,[],hs),'b',Tideal,'r--',0.5); grid on legend('Tlpv','Tideal')

The closed-loop system has additional zeros not in the ideal response Tideal. These zeros arise from the PID controller and cause a shorter rise time and larger overshoot.
You can use a two degree-of-freedom architecture with a reference prefilter Fref to reduce the overshoot. Model the prefilter as an LTI system for simplicity.
Fref = ss(-10,10,1,0); step(sample(Tlpv*Fref,[],hs),'b',Tideal,'r--',0.5); grid on; legend('Tlpv','Tideal','Location','Southeast');

LPV Simulations
To approximate the nonlinear closed-loop response, simulate the transient response of the closed-loop LPV model with a pre-filter. This requires you to specify the parameter trajectory , which is not known beforehand. As a proxy, you can set to the ideal response produced by Tideal*Fref.
CL = Tlpv*Fref;
Set the initial height and step signal parameters.
h0 = (hmin+hmax)/2; tstep = 0.2; Tf = 1.2; hStepAmp = 0.25*h0;
Set to ideal trajectory and simulate the response.
t = linspace(0,tstep+Tf,100); StepConfig = RespConfig('Bias',h0,'Delay',tstep,'Amplitude',hStepAmp); p_ideal = step(Tideal*Fref,t,StepConfig); y1 = step(CL,t,p_ideal,StepConfig);
Alternatively, to use the true trajectory, you can specify implicitly as a function of time , input , and state . Here is just the first state.
Set and simulate the step response.
pFcn = @(t,x,u) x(1); StepConfig = RespConfig('Bias',h0,'Delay',tstep,... 'Amplitude',hStepAmp,'InitialParameter',h0); y2 = step(CL,t,pFcn,StepConfig);
Plot and compare the two responses.
plot(t,y1,t,y2); legend('p ideal','p true','Location','Southeast'); grid

The two responses are close to each other. The Simulink-based counterpart of this example shows that the nonlinear response is well approximated by both LPV simulations with a small edge for the simulation with true trajectory.
Plant Data Function
type dataFcnMaglev.mfunction [A,B,C,D,E,dx0,x0,u0,y0,Delays] = dataFcnMaglev(~,p) % MAGLEV example: % x = [h ; dh/dt] % p=hbar (equilibrium height) mb = 0.02; % kg g = 9.81; alpha = 2.4832e-5; A = [0 1;2*g/p 0]; B = [0 ; -2*sqrt(g*alpha/mb)/p]; C = [1 0]; % h D = 0; E = []; dx0 = []; x0 = [p;0]; u0 = sqrt(mb*g/alpha)*p; % ibar y0 = p; % y = h = hbar + (h-hbar) Delays = [];
See Also
lpvss | sample | step | RespConfig