closestPointsToSequence
Syntax
Description
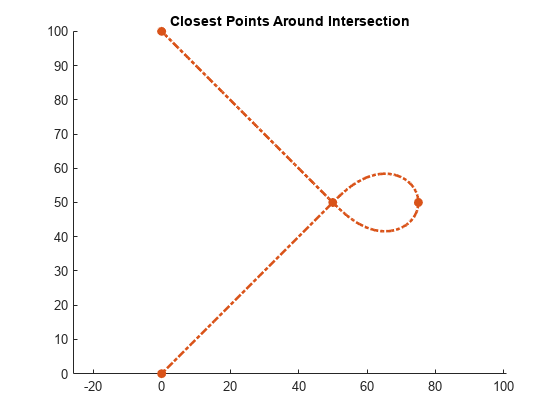
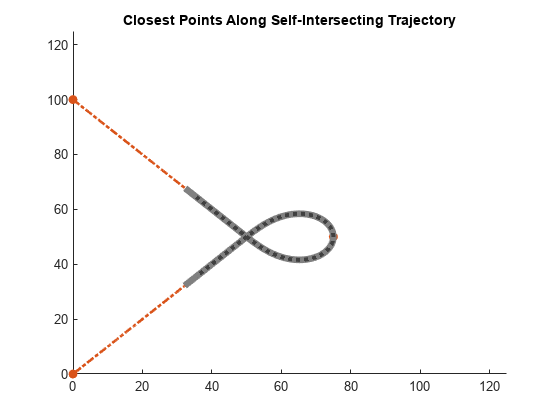
pathPoints = closestPointsToSequence(refPath,points,initWindow)points, to be
within the valid search window, initWindow. For each point in
Points, the search window is centered at the previous point.
[
optionally returns a logical vector pathPoints,inWindow] = closestPointsToSequence(refPath,points,initWindow)inWindow, specifying whether each
point for the corresponding xy coordinate in points
is projected within the search window.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2022a