global2frenet

Convert global states to Frenet states

Since R2020b

Syntax

frenetState = global2frenet(refPath,globalState)

[___,latTimeDerivatives] = global2frenet(refPath,globalState)

[___] = global2frenet(refPath,globalState,sFrame)

Description

frenetState = global2frenet(refPath,globalState) converts global states to Frenet trajectory states.

[___,latTimeDerivatives] = global2frenet(refPath,globalState) returns latTimeDerivatives containing first and second-order derivatives of lateral deviation with respect to time and a flag indicating if the heading should flip when converting to global coordinates.

[___] = global2frenet(refPath,globalState,sFrame) accepts a vector of arc lengths, sFrame at which the Frenet frame should be centered at.

Examples

Generate Trajectory from Reference Path

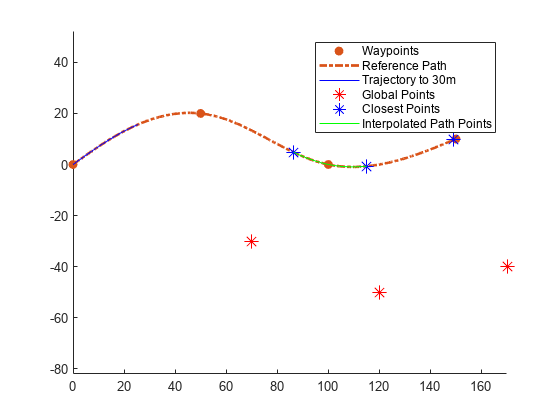
Generate a reference path from a set of waypoints.

waypoints = [0 0; 50 20; 100 0; 150 10];
refPath = referencePathFrenet(waypoints);

Create a trajectoryGeneratorFrenet object from the reference path.

connector = trajectoryGeneratorFrenet(refPath);

Generate a five-second trajectory between the path origin and a point 30 meters down the path as Frenet states.

initCartState = refPath.SegmentParameters(1,:);
initFrenetState = global2frenet(refPath,initCartState);
termFrenetState = initFrenetState + [30 zeros(1,5)];
frenetTraj = connect(connector,initFrenetState,termFrenetState,5);

Convert the trajectory to the global states.

globalTraj = frenet2global(refPath,frenetTraj.Trajectory);

Display the reference path and the trajectory.

show(refPath);
axis equal
hold on
plot(globalTraj(:,1),globalTraj(:,2),'b')

Specify global points and find the closest points on reference path.

globalPoints = waypoints(2:end,:) + [20 -50];
nearestPathPoint = closestPoint(refPath,globalPoints);

Display the global points and the closest points on reference path.

plot(globalPoints(:,1),globalPoints(:,2),'r*','MarkerSize',10)
plot(nearestPathPoint(:,1),nearestPathPoint(:,2),'b*','MarkerSize',10)

Interpolate between the arc lengths of the first two closest points along the reference path.

arclengths = linspace(nearestPathPoint(1,6),nearestPathPoint(2,6),10);
pathStates = interpolate(refPath,arclengths);

Display the interpolated path points.

plot(pathStates(:,1),pathStates(:,2),'g')
legend(["Waypoints","Reference Path","Trajectory to 30m",...
        "Global Points","Closest Points","Interpolated Path Points"])

Input Arguments

refPath — Reference path

referencePathFrenet object

Reference path, specified as a referencePathFrenet object.

globalState — States in global coordinate frame

P-by-6 numeric matrix

States in the global coordinate frame, specified as a P-by-6 numeric matrix with rows of form [x y theta kappa speed accel], where:

• x y and theta –– SE(2) state expressed in global coordinates, with x and y in meters and theta in radians.

• kappa –– Curvature, or inverse of the radius, in m-1.

• speed –– Speed in the theta direction in m/s.

• accel –– Acceleration in the theta direction in m/s2.

P is the total number of Global states.

sFrame — Arc length frame locations

N-element vector

Arc length center locations for the Frenet frames, specified as an N-element vector in meters. For correct results, the vector between the frame and the xy location of the globalState must be orthogonal to the tangent angle.

Output Arguments

frenetState — States in Frenet coordinate frame

P-by-6 numeric matrix

States in the Frenet coordinate frame, returned as a P-by-6 numeric matrix with rows of form [S dS ddS L dL ddL], where S is the arc length and L is the perpendicular deviation from the direction of the reference path. Derivatives of S are relative to time. Derivatives of L are relative to the arc length, S. P is the total number of Frenet states.

latTimeDerivatives — Lateral time derivatives

N-by-3 matrix

Lateral time derivatives, specified as an N-by-3 matrix where each row is of the form [dL/dt ddL/dt^2 invertHeading] and N is the total number of points in points. Each row contains the 1st and 2nd order time derivatives of lateral deviation and a flag, invertHeading, which indicates whether the heading should be flipped when converting to global coordinates (true) or not (false).

Note

If defining latTimeDerivatives without the use of global2frenet, the following rules should be followed:

1. The invertHeading flag should be true when:

   1. The vehicle is moving in reverse (speed is less than 0)

   2. The vehicle is stationary (speed is equal to 0), and the vehicle is facing away from the path's tangent vector. i.e. cos(|tangentAngle(obj,S)-thetaExpected|) < 0

2. If 1b is true, then dL/dS must be negated.

More About

Frenet Coordinate System Conversions

• The global2frenet object function finds a point [x y]p along the path that is closest to the xy-coordinate of the global state [x y theta kappa speed accel]g. Since the reference path is C1 continuous (tangentially continuous), the distance will be shortest, where [x y]g-[x y]p is orthogonal to the tangent of the path.

  where:

  • x y and theta –– SE(2) state expressed in global coordinates, with x and y in meters and theta in radians.

  • kappa –– Curvature, or inverse of the radius, in m-1.

  • speed –– Speed in the theta direction in m/s.

  • accel –– Acceleration in the theta direction in m/s2.

• The function then evaluates the full state of the path [x y theta kappa dkappa s]p. This is equivalent to a moving reference frame located at [x y]p whose longitudinal axis points along thetap and lateral axis intersects with [x y]g (right-hand rule). The instantaneous motion of this frame is described by [kappa dkappa]p.

  where:

  • x y and theta — SE(2) state expressed in global coordinates, with x and y in meters and theta in radians.

  • kappa — Curvature, or inverse of the radius, in m-1.

  • dkappa — Derivative of curvature with respect to arc length in m-2.

  • s — Arc length, or distance along path from path origin, in meters.

  

• The velocity and acceleration components of the global state act along the tangent defined by thetag, which itself evolves based on kappag. The function then maps the global position, velocity, and acceleration to the local Frenet frame and returns the Frenet state, [s ds dds L dL ddL]f.

  where:

  • s — Arc length, or distance along path from path origin, in meters.

  • L — Perpendicular deviation from the direction of the reference path, in meters.

  • ds and dds — Derivatives of s relative to time.

  • dL and ddL — Derivatives of L relative to the arc length, s.

  

• The process for the frenet2global function is the inverse of the global2frenet function.

• The frenet2global function evaluates the path at the arc length of the Frenet state, sf=sp, returning [x y theta kappa dkappa s]p.

• This point once again defines a reference frame whose axes and motion can be used to project the lateral or longitudinal deviations and their first and second-order derivatives back into the global frame.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2020b