paretotails
Piecewise distribution with Pareto tails
Description
A paretotails object is a piecewise distribution with
generalized Pareto distributions (GPDs) in the tails.
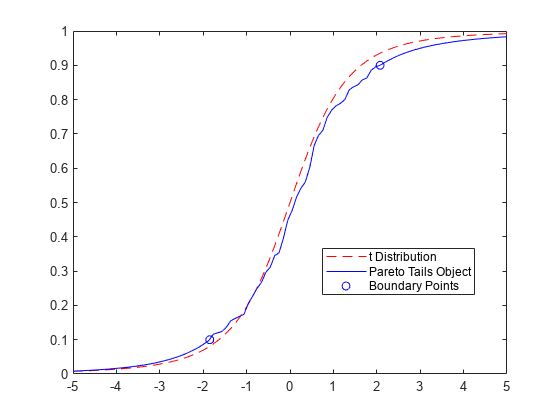
A paretotails object consists of one or two GPDs in the tails and
another distribution in the center. You can specify the distribution type for the center
by using the cdffun argument of paretotails when
you create an object. Valid values are 'ecdf',
'kernel', and a function handle.
paretotails fits a distribution of type cdffun
to the observations (x) and finds the quantiles corresponding to
the lower and upper tail cumulative probabilities (pl and
pu, respectively). Then, paretotails fits two
GPDs to the lower 100*pl percent of the observations and the upper
100*(1–pu) percent of the observations, respectively. If
x does not have at least two distinct observations in a tail,
then paretotails does not create the corresponding tail segment.
Use the object functions boundary, segment, upperparams, and lowerparams to find distribution characteristics. lowerparams and upperparams return the parameters of the GPDs in the tails. boundary returns the boundary points between piecewise distribution
segments, segment returns the segment of a
piecewise distribution containing input values, and nsegments returns the number of segments in an object.
Use the object functions cdf, icdf, pdf, and random to evaluate the distribution. These functions are well suited to
copula and other Monte Carlo simulations. pdf returns the GPD
density in the tails and the slope of the cumulative distribution function (cdf) in the
center. These probability density function (pdf) values in the center are generally not
good estimates of the underlying density of the original data.
Creation
Create a piecewise distribution object using paretotails.
Description
Input Arguments
Properties
Object Functions
boundary | Piecewise distribution boundaries |
cdf | Cumulative distribution function |
icdf | Inverse cumulative distribution function |
lowerparams | Lower Pareto tail parameters |
nsegments | Number of segments in piecewise distribution |
pdf | Probability density function |
random | Random numbers |
segment | Piecewise distribution segments containing input values |
upperparams | Upper Pareto tail parameters |
Examples
Version History
Introduced in R2007a