disparateImpactRemover
Description
To try to create fairness in binary classification, you can use the
disparateImpactRemover function to remove or reduce the disparate
impact of a sensitive attribute. Before training your model, use the sensitive attribute to
transform the continuous predictors in the training data set. The function returns the
transformed data set and a disparateImpactRemover object that contains the
transformation. Pass the transformed data set to an appropriate training function, such as
fitcsvm, and pass the object to the transform object
function to apply the transformation to a new data set, such as a test data
set.
Note
You must transform new data, such as test data, after training a model using
disparateImpactRemover. Otherwise, the predicted results are
inaccurate.
Creation
Syntax
Description
remover = disparateImpactRemover(Tbl,AttributeName)AttributeName sensitive attribute
in the table Tbl by transforming the continuous predictors in the
data set Tbl. The returned disparateImpactRemover
object (remover) stores the transformation, which you can apply to
new data. For more information, see Algorithms.
[
also returns the transformed predictor data remover,transformedData] = disparateImpactRemover(Tbl,AttributeName)transformedData, which
corresponds to the data in Tbl.
Note that transformedData includes the sensitive attribute in
this syntax. After using disparateImpactRemover, avoid using the
sensitive attribute as a separate predictor when training your model.
[
uses the numeric predictor data remover,transformedData] = disparateImpactRemover(X,attribute)X and the sensitive attribute
specified by attribute to transform the predictors.
[
specifies options using one or more name-value arguments in addition to any of the input
argument combinations in previous syntaxes. For example, you can specify the extent of the
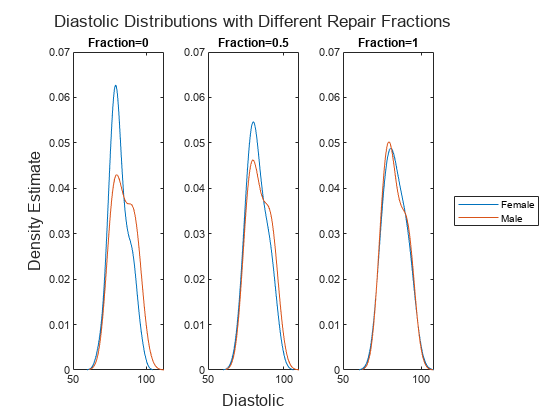
data transformation by using the remover,transformedData] = disparateImpactRemover(___,Name=Value)RepairFraction name-value argument.
A value of 1 indicates a full transformation, and a value of 0 indicates no
transformation.
Input Arguments
Name-Value Arguments
Output Arguments
Properties
Object Functions
transform | Transform new predictor data to remove disparate impact |
Examples
More About
Tips
After using
disparateImpactRemover, consider using only continuous and ordinal predictors for model training. Avoid using the sensitive attribute as a separate predictor when training your model. For more information, see [1].You must transform new data, such as test data, after training a model using
disparateImpactRemover. Otherwise, the predicted results are inaccurate. Use thetransformobject function.
Algorithms
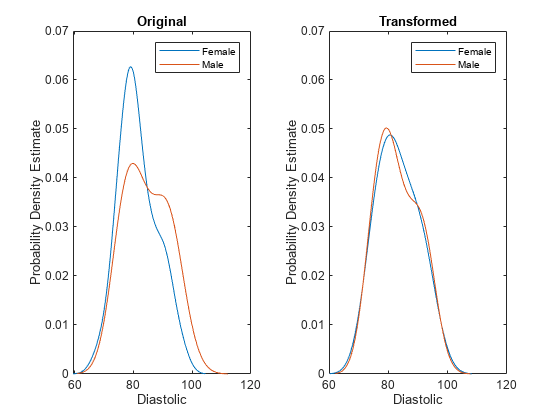
disparateImpactRemover transforms a continuous predictor in
Tbl or X as follows:
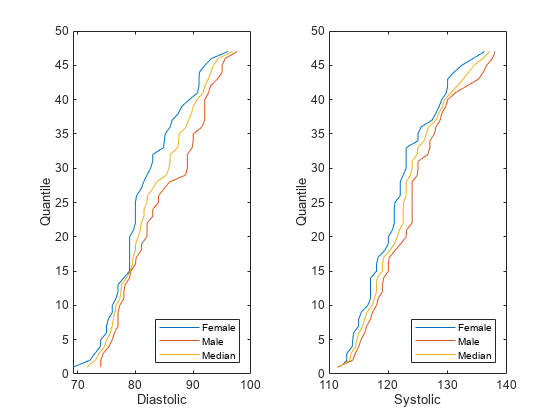
The software uses the groups in the sensitive attribute to split the predictor values. For each group g, the software computes q quantiles of the predictor values by using the
quantilefunction. The number of quantiles q is either 100 or the minimum number of group observations across the groups in the sensitive attribute, whichever is smaller. The software creates a corresponding binning function Fg using thediscretizefunction and the quantile values as bin edges.The software then finds the median quantile values across all the sensitive attribute groups and forms the associated quantile function Fm-1. The software omits missing (
NaN) values from this calculation.Finally, the software transforms the predictor value x in the sensitive attribute group g by using the transformation λFm-1(Fg(x)) + (1 – λ)x, where λ is the repair fraction
RepairFraction. The software preserves missing (NaN) values in the predictor.
The function stores the transformation, which you can apply to new predictor data.
For more information, see [1].
References
[1] Feldman, Michael, Sorelle A. Friedler, John Moeller, Carlos Scheidegger, and Suresh Venkatasubramanian. “Certifying and Removing Disparate Impact.” In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 259–68. Sydney NSW Australia: ACM, 2015. https://doi.org/10.1145/2783258.2783311.
Version History
Introduced in R2022b