New to r2020a, leapseconds() creates a table showing all leap seconds recognized by the datetime data type.
>> leapseconds()
ans =
27×2 timetable
Date Type CumulativeAdjustment
___________ ____ ____________________
30-Jun-1972 + 1 sec
31-Dec-1972 + 2 sec
31-Dec-1973 + 3 sec
31-Dec-1974 + 4 sec
31-Dec-1975 + 5 sec
<< 21 rows removed >>
31-Dec-2016 + 27 sec
Leap seconds can covertly sneak into your data and cause errors that are difficult to resolve if the leap seconds go undetected. A leap second was responsible for crashing Reddit , Mozilla, Yelp, LinkedIn and other sites in 2012.
Detect leap seconds present in a vector of years
% Define a vector of years t = 2005:2008;
allLeapSeconds = leapseconds(); isYearWithLeapSecond = ismember(t,year(allLeapSeconds.Date));
% Show years that contain a leap second
t(isYearWithLeapSecond)
ans =
2005 2008
Detect leap seconds present in a vector of months
% Define a vector of months t = datetime(1972, 1, 1) + calmonths(0:11);
t.Format = 'MMM-yyyy'; allLeapSeconds = leapseconds(); [tY,tM] = ymd(t); [leapSecY, leapSecM] = ymd(allLeapSeconds.Date); isMonthWithLeapSecond = ismember([tY(:),tM(:)], [leapSecY, leapSecM], 'rows');
% Show months that contain a leap second t(isMonthWithLeapSecond) ans = 1×2 datetime array Jun-1972 Dec-1972
List all leap seconds in your lifetime
% Enter your birthday in mm/dd/yyyy hh:mm:ss format yourBirthday = '01/15/1988 14:30:00';
yourTimeRange = timerange(datetime(yourBirthday), datetime('now'));
allLeapSeconds = leapseconds();
lifeLeapSeconds = allLeapSeconds(yourTimeRange,:);
lifeLeapSeconds.YourAge = lifeLeapSeconds.Date - datetime(yourBirthday);
lifeLeapSeconds.YourAge.Format = 'y';
% Show table
fprintf('\n Leap seconds in your lifetime:\n')
disp(lifeLeapSeconds)
Leap seconds in your lifetime:
Date Type CumulativeAdjustment YourAge
___________ ____ ____________________ __________
31-Dec-1989 + 15 sec 1.9587 yrs
31-Dec-1990 + 16 sec 2.958 yrs
<< 8 rows removed >>
30-Jun-2012 + 25 sec 24.456 yrs
30-Jun-2015 + 26 sec 27.454 yrs
31-Dec-2016 + 27 sec 28.96 yrs
What is a leap second?
A second is defined as the time it takes a cesium-133 atom to oscillate 9,192,631,770 times under controlled conditions. The transition frequency is so precise that it takes 100 million years to gain 1 second of error [1]. If the earth’s rotation were perfectly synchronized to the atomic second, a day would be 86,400 seconds. But the earth’s rate of rotation is affected by climate, winds, atmospheric pressure, and the rate of rotation is gradually decreasing due to tidal friction [2,3]. Several months before the expected difference between the atomic clock-based time (UTC) and universal time (UT1) reaches +/- 0.9 seconds the IERS authorizes the addition (or subtraction) of 1 leap second (see plot below). Since the first leap second in 1972, all leap second adjustments have been made on the last day of June or December and all adjustments have been +1 second which explains the + signs in the type column of the leapseconds() table.
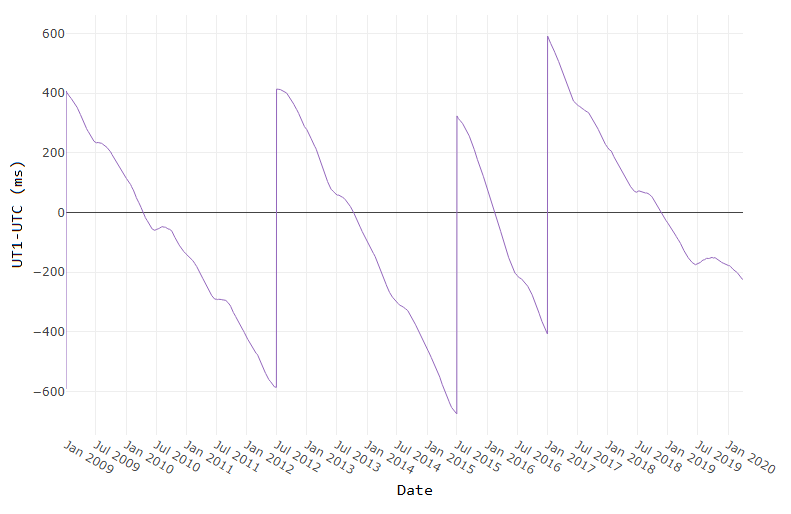
[ Image source ]
How to reference the leap second schedule in your code
Since leap second adjustments are not regularly timed, you can record the official IERS Bulletin C version used at the time of your analysis by accessing the 2nd output to leapseconds().
[T,vers] = leapseconds
What do leap seconds look like in datetime values?
A minute typically has 60 seconds spanning from 0:59. A minute containing a leap second has 61 seconds spanning from 0:60.
December 30, 2016 was a normal day. If we add the usual 86400 seconds to the start of that day, the result is the start of the next day.
d = datetime(2016, 12, 30, 'TimeZone','UTCLeapSeconds') + seconds(86400) d = datetime 2016-12-31T00:00:00.000Z
The next day, December 31, 2016, had a leap second. If we add 86400 seconds to the start of that day, the result is not the start of the next day.
d = datetime(2016, 12, 31, 'TimeZone','UTCLeapSeconds') + seconds(86400) d = datetime 2016-12-31T23:59:60.000Z
When will the next leap second be?
As of the current date (April 2020) the timing of the next leap second is unknown. Based on the data from the plot above, what's your guess?
References
