resnetLayers

(Not recommended) Create 2-D residual network

Since R2021b

resnetLayers is not recommended. Use the resnetNetwork function instead. For more information, see Version History.

Syntax

lgraph = resnetLayers(inputSize,numClasses)

lgraph = resnetLayers(___,Name=Value)

Description

lgraph = resnetLayers(inputSize,numClasses) creates a 2-D residual network with an image input size specified by inputSize and a number of classes specified by numClasses.

lgraph = resnetLayers(___,Name=Value) creates a residual network using one or more name-value arguments using any of the input arguments in the previous syntax. For example, InitialNumFilters=32 specifies 32 filters in the initial convolutional layer.

Tip

To load a pretrained ResNet neural network, use the imagePretrainedNetwork function.

Examples

Create Residual Network

Create a residual network.

Create a residual network with a bottleneck architecture.

imageSize = [224 224 3];
numClasses = 10;

lgraph = resnetLayers(imageSize,numClasses)

lgraph = 
  LayerGraph with properties:

     InputNames: {'input'}
    OutputNames: {'output'}
         Layers: [177x1 nnet.cnn.layer.Layer]
    Connections: [192x2 table]

This network is equivalent to a ResNet-50 residual network.

Input Arguments

inputSize — Network input image size

2-element vector | 3-element vector

Network input image size, specified as one of the following:

• 2-element vector in the form [height, width].

• 3-element vector in the form [height, width, depth], where depth is the number of channels. Set depth to 3 for RGB images and to 1 for grayscale images. For multispectral and hyperspectral images, set depth to the number of channels.

The height and width values must be greater than or equal to initialStride * poolingStride * 2^D, where D is the number of downsampling blocks. Set the initial stride using the InitialStride argument. The pooling stride is 1 when the InitialPoolingLayer is set to "none", and 2 otherwise.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

numClasses — Number of classes

integer greater than 1

Number of classes in the image classification network, specified as an integer greater than 1.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: InitialFilterSize=[5,5],InitialNumFilters=32,BottleneckType="none" specifies an initial filter size of 5-by-5 pixels, 32 initial filters, and a network architecture without bottleneck components.

Initial Layers

InitialFilterSize — Filter size in first convolutional layer

7 (default) | positive integer | 2-element vector of positive integers

Filter size in the first convolutional layer, specified as one of the following:

• Positive integer. The filter has equal height and width. For example, specifying 5 yields a filter of height 5 and width 5.

• 2-element vector in the form [height, width]. For example, specifying an initial filter size of [1 5] yields a filter of height 1 and width 5.

Example: InitialFilterSize=[5,5]

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

InitialNumFilters — Number of filters in first convolutional layer

64 (default) | positive integer

Number of filters in the first convolutional layer, specified as a positive integer. The number of initial filters determines the number of channels (feature maps) in the output of the first convolutional layer in the residual network.

Example: InitialNumFilters=32

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

InitialStride — Stride in first convolutional layer

2 (default) | positive integer | 2-element vector of positive integers

Stride in the first convolutional layer, specified as a:

• Positive integer. The stride has equal height and width. For example, specifying 3 yields a stride of height 3 and width 3.

• 2-element vector in the form [height, width]. For example, specifying an initial stride of [1 2] yields a stride of height 1 and width 2.

The stride defines the step size for traversing the input vertically and horizontally.

Example: InitialStride=[3,3]

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

InitialPoolingLayer — First pooling layer

"max" (default) | "average" | "none"

First pooling layer before the initial residual block, specified as one of the following:

• "max" — Use a max pooling layer before the initial residual block. For more information, see maxPooling2dLayer.

• "average" — Use an average pooling layer before the initial residual block. For more information, see averagePooling2dLayer.

• "none"— Do not use a pooling layer before the initial residual block.

Example: InitialPoolingLayer="average"

Data Types: char | string

Network Architecture

ResidualBlockType — Residual block type

"batchnorm-before-add" (default) | "batchnorm-after-add"

Residual block type, specified as one of the following:

• "batchnorm-before-add" — Add the batch normalization layer before the addition layer in the residual blocks [1].

• "batchnorm-after-add" — Add the batch normalization layer after the addition layer in the residual blocks [2].

The ResidualBlockType argument specifies the location of the batch normalization layer in the standard and downsampling residual blocks. For more information, see More About.

Example: ResidualBlockType="batchnorm-after-add"

Data Types: char | string

BottleneckType — Block bottleneck type

"downsample-first-conv" (default) | "none"

Block bottleneck type, specified as one of the following:

• "downsample-first-conv" — Use bottleneck residual blocks that perform downsampling in the first convolutional layer of the downsampling residual blocks, using a stride of 2. A bottleneck residual block consists of three convolutional layers: a 1-by-1 layer for downsampling the channel dimension, a 3-by-3 convolutional layer, and a 1-by-1 layer for upsampling the channel dimension.

  The number of filters in the final convolutional layer is four times that in the first two convolutional layers. For more information, see NumFilters.

• "none" — Do not use bottleneck residual blocks. The residual blocks consist of two 3-by-3 convolutional layers.

A bottleneck block performs a 1-by-1 convolution before the 3-by-3 convolution to reduce the number of channels by a factor of four. Networks with and without bottleneck blocks will have a similar level of computational complexity, but the total number of features propagating in the residual connections is four times larger when you use bottleneck units. Therefore, using a bottleneck increases the efficiency of the network [1]. For more information on the layers in each residual block, see More About.

Example: BottleneckType="none"

Data Types: char | string

StackDepth — Number of residual blocks in each stack

[3 4 6 3] (default) | vector of positive integers

Number of residual blocks in each stack, specified as a vector of positive integers. For example, if the stack depth is [3 4 6 3], the network has four stacks, with three blocks, four blocks, six blocks, and three blocks.

Specify the number of filters in the convolutional layers of each stack using the NumFilters argument. The StackDepth value must have the same number of elements as the NumFilters value.

Example: StackDepth=[9 12 69 9]

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

NumFilters — Number of filters in convolutional layers of each stack

[64 128 256 512] (default) | vector of positive integers

Number of filters in the convolutional layers of each stack, specified as a vector of positive integers.

• When you set BottleneckType to "downsample-first-conv", the first two convolutional layers in each block of each stack have the same number of filters, set by the NumFilters value. The final convolutional layer has four times the number of filters in the first two convolutional layers.

  For example, suppose you set NumFilters to [4 5] and BottleneckType to "downsample-first-conv". In the first stack, the first two convolutional layers in each block have 4 filters and the final convolutional layer in each block has 16 filters. In the second stack, the first two convolutional layers in each block have 5 filters and the final convolutional layer has 20 filters.

• When you set BottleneckType to "none", the convolutional layers in each stack have the same number of filters, set by the NumFilters value.

The NumFilters value must have the same number of elements as the StackDepth value.

The NumFilters value determines the layers on the residual connection in the initial residual block. There is a convolutional layer on the residual connection if one of the following conditions is met:

• BottleneckType="downsample-first-conv"(default) and InitialNumFilters is not equal to four times the first element of NumFilters.

• BottleneckType="none" and InitialNumFilters is not equal to the first element of NumFilters.

For more information about the layers in each residual block, see More About.

Example: NumFilters=[32 64 126 256]

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Normalization — Data normalization

"zerocenter" (default) | "zscore"

Data normalization to apply every time data is forward-propagated through the input layer, specified as one of the following:

• "zerocenter" — Subtract the mean. The mean is calculated at training time.

• "zscore" — Subtract the mean and divide by the standard deviation. The mean and standard deviation are calculated at training time.

Example: Normalization="zscore"

Data Types: char | string

Output Arguments

lgraph — Residual network

layerGraph object

Residual network, returned as a layerGraph object.

More About

Residual Network

Residual networks (ResNets) are a type of deep network that consist of building blocks that have residual connections (also known as skip or shortcut connections). These connections allow the input to skip the convolutional units of the main branch, thus providing a simpler path through the network. By allowing the parameter gradients to flow more easily from the final layers to the earlier layers of the network, residual connections help mitigate the problem of vanishing gradients during early training.

The structure of a residual network is flexible. The key component is the inclusion of the residual connections within residual blocks. A group of residual blocks is called a stack. A ResNet architecture consists of initial layers, followed by stacks containing residual blocks, and then the final layers. A network has three types of residual blocks:

• Initial residual block — This block occurs at the start of the first stack. The layers in the residual connection of the initial residual block determine if the block preserves the activation sizes or performs downsampling.

• Standard residual block — This block occurs multiple times in each stack, after the first downsampling residual block. The standard residual block preserves the activation sizes.

• Downsampling residual block — This block occurs once, at the start of each stack. The first convolutional unit in the downsampling block downsamples the spatial dimensions by a factor of two.

A typical stack has a downsampling residual block, followed by m standard residual blocks, where m is a positive integer. The first stack is the only stack that begins with an initial residual block.

The initial, standard, and downsampling residual blocks can be bottleneck or nonbottleneck blocks. Bottleneck blocks perform a 1-by-1 convolution before the 3-by-3 convolution, to reduce the number of channels by a factor of four.​ Networks with and without bottleneck blocks have a similar level of computational complexity, but the total number of features propagating in the residual connections is four times larger when you use the bottleneck units. Therefore, using bottleneck blocks increases the efficiency of the network.

The layers inside each block are determined by the type of block and the options you set.

Block Layers

Name	Initial Layers	Initial Residual Block	Standard Residual Block (BottleneckType="downsample-first-conv")	Standard Residual Block (BottleneckType="none")	Downsampling Residual Block	Final Layers
Description	A residual network starts with the following layers, in order: imageInputLayer convolution2dLayer batchNormalizationLayer reluLayer (Optional) Pooling layer (either max, average, or none) Set the optional pooling layer using the InitialPoolingLayer argument.	The main branch of the initial residual block has the same layers as a standard residual block. The InitialNumFilters and NumFilters values determine the layers on the residual connection. The residual connection has a convolutional layer with [1,1] filter and [1,1] stride if one of the following conditions is met: BottleneckType="downsample-first-conv"(default) and InitialNumFilters is not equal to four times the first element of NumFilters. BottleneckType="none" and InitialNumFilters is not equal to the first element of NumFilters. If ResidualBlockType is set to"batchnorm-before-add", the residual connection will also have a batch normalization layer.	The standard residual block with bottleneck units has the following layers, in order: convolution2dLayer with [1,1] filter and [1,1] stride batchNormalizationLayer reluLayer convolution2dLayer with [3,3] filter and [1,1] stride batchNormalizationLayer reluLayer convolution2dLayer with [1,1] filter and [1,1] stride batchNormalizationLayer additionLayer reluLayer The standard block has a residual connection from the output of the previous block to the addition layer. Set the position of the addition layer using the ResidualBlockType argument.	The standard residual block without bottleneck units has the following layers, in order: convolution2dLayer with [3,3] filter and [1,1] stride batchNormalizationLayer reluLayer convolution2dLayer with [3,3] filter and [1,1] stride batchNormalizationLayer additionLayer reluLayer The standard block has a residual connection from the output of the previous block to the addition layer. Set the position of the addition layer using the ResidualBlockType argument.	The downsampling residual block is the same as the standard block (either with or without the bottleneck) but with a stride of [2,2] in the first convolutional layer and additional layers on the residual connection. The layers on the residual connection depend on the ResidualBlockType value. When ResidualBlockType is set to "batchnorm-before-add", the second branch contains a convolution2dLayer with [1,1] filter and [2,2] stride, and a batchNormalizationLayer. When ResidualBlockType is set to "batchnorm-after-add", the second branch contains a convolution2dLayer with [1,1] filter and [2,2] stride. The downsampling block halves the height and width of the input, and increases the number of channels.	A residual network ends with the following layers, in order: globalAveragePooling2dLayer fullyConnectedLayer softmaxLayer classificationLayer
Example Visualization		Example of an initial residual block for a network without a bottleneck and with the batch normalization layer before the addition layer.	Example of the standard residual block for a network with a bottleneck and with the batch normalization layer before the addition layer.	Example of the standard residual block for a network without a bottleneck and with the batch normalization layer before the addition layer.	Example of a downsampling residual block for a network without a bottleneck and with the batch normalization layer before the addition layer.

The convolution and fully connected layer weights are initialized using the He weight initialization method [3]. For more information, see convolution2dLayer.

Tips

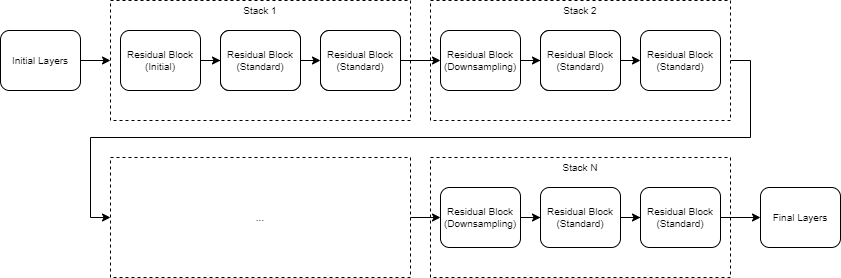
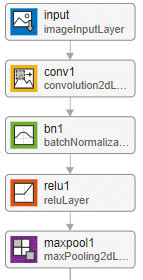
• When working with small images, set the InitialPoolingLayer option to "none" to remove the initial pooling layer and reduce the amount of downsampling.

• Residual networks are usually named ResNet-X, where X is the depth of the network. The depth of a network is defined as the largest number of sequential convolutional or fully connected layers on a path from the input layer to the output layer. You can use the following formula to compute the depth of your network:

  $$\text{depth = }\{\begin{array}{c}1+2{\displaystyle \sum }_{i=1}^N{s}_i+1\text{ If no bottleneck}\\ 1+3{\displaystyle \sum }_{i=1}^N{s}_i+1\text{ If bottleneck}\end{array}\text{ ,}$$

  where s_i is the depth of stack i.

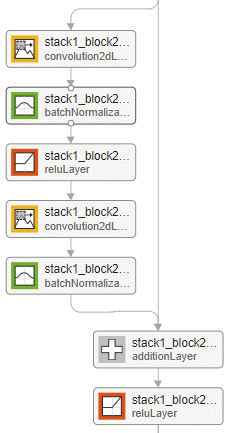
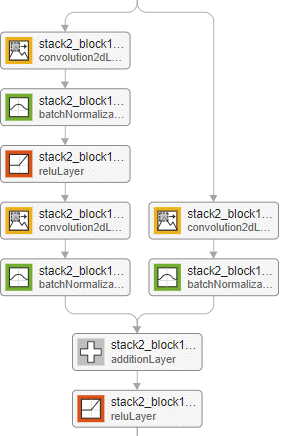
  Networks with the same depth can have different network architectures. For example, you can create a ResNet-14 architecture with or without a bottleneck:

  resnet14Bottleneck = resnetLayers([224 224 3],10, ...
  StackDepth=[2 2], ...
  NumFilters=[64 128]);
  
  resnet14NoBottleneck = resnetLayers([224 224 3],10, ...
  BottleneckType="none", ...
  StackDepth=[2 2 2], ...
  NumFilters=[64 128 256]);

  The relationship between bottleneck and nonbottleneck architectures also means that a network with a bottleneck will have a different depth than a network without a bottleneck.

  resnet50Bottleneck = resnetLayers([224 224 3],10);
  
  resnet34NoBottleneck = resnetLayers([224 224 3],10, ... 
  BottleneckType="none");
  

References

[1] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. “Deep Residual Learning for Image Recognition.” Preprint, submitted December 10, 2015. https://arxiv.org/abs/1512.03385.

[2] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. “Identity Mappings in Deep Residual Networks.” Preprint, submitted July 25, 2016. https://arxiv.org/abs/1603.05027.

[3] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification." In Proceedings of the 2015 IEEE International Conference on Computer Vision, 1026–1034. Washington, DC: IEEE Computer Vision Society, 2015.

Extended Capabilities

GPU Code Generation

Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

You can use the residual network for code generation. First, create the network using the resnetLayers function. Then, use the trainNetwork function to train the network. After training and evaluating the network, you can generate code for the DAGNetwork object by using GPU Coder™.

Version History

Introduced in R2021b

R2024a: Not recommended

Starting in R2024a, resnetLayers is not recommended, use resnetNetwork instead.

There are no plans to remove support for resnetLayers. However, resnetNetwork returns a dlnetwork object, which has these advantages and is recommended instead:

• dlnetwork objects are a unified data type that supports network building, prediction, built-in training, visualization, compression, verification, and custom training loops.

• dlnetwork objects support a wider range of network architectures that you can create or import from external platforms.

• The trainnet function supports dlnetwork objects, which enables you to easily specify loss functions. You can select from built-in loss functions or specify a custom loss function.

• Training and prediction with dlnetwork objects is typically faster than LayerGraph and trainNetwork workflows.

The resnetNetwork function has the same syntaxes and arguments as the resnetLayers function. This table shows some typical usages of the resnetLayers function and how to update your code to use the resnetNetwork function instead.

Not Recommended	Recommended
lgraph = resnetLayers(inputSize,numClasses);	net = resnetNetwork(inputSize,numClasses);
lgraph = resnetLayers(inputSize,numClasses,BottleneckType="none");	net = resnetNetwork(inputSize,numClasses,BottleneckType="none");